6、已知⊙O₁和⊙O₂相内切，且⊙O₁的半径为6，两圆的圆心距为3，则⊙O₂的半径为_____。

5、⊙O的半径为5，AB、CD为⊙O的两条弦，且AB∥CD，AB＝6，CD＝8，则AB与CD之间的距离为_____。

4、已知两个等圆⊙O₁和⊙O₂相交于A、B两点，⊙O₁经过点O₂，则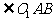的度数是_____。

3、⊙O与⊙O’相交于点A、B，，⊙O和⊙O’的半径分别为4和3，则公共弦AB的长为_____。

2、若圆的半径为2，圆中一条弦长为，则此弦中点到此弦所对劣弧的中点的距离为_____。

1、若⊙O的半径为5，弦AB的长为8，则圆心O到AB的距离是_____。

例1、　　 已知两圆的半径R，r(R≥r)是方程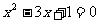的两个根，两圆的圆心距为d，

(1)若d＝4，试判定两圆的位置关系；

(2)若d＝2，试判定两圆的位置关系；

(3)若两圆相交，试确定d的取值范围；

(4)若两圆相切，求d的值。

解：∵R，r是方程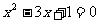的两根

∴R+r＝3，R·r＝1

则，

(1)∵d＝4　　　　 ∴d＞R+r，则两圆外离；

(2)∵d＝2　　　　 ∴d＜R－r，则两圆内含；

(3)∵两圆相交　　　 ∴R－r＜d＜R+r，即：＜d＜3

(4)∵两圆相切　　 　∴d＝R+r或d＝R－r，即：d＝3或d＝

注意：两圆相切有两种可能(内切或外切)

例2：如图(4)，⊙o₁与⊙o₂相交于A、B，直线Ao₁交⊙o₁于C，交⊙o₂于D，CB的延长线交⊙o₂于E，若CD＝10，DE＝6，求⊙o₂的长。

解：连结AB、AE

AC为⊙o₁的直径　

ABCD内接于⊙o₂

AE为⊙o₂的直径o₂为AE中点 　　

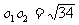
　　　　　　　　 o₁为AC中点

在中，　

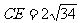
　　　　　　　 CD＝10，DE＝6

注意：两圆相交时，常添公共弦、连心线等作为辅助线，这些辅助线能把两圆中的角或线段联系起来，起到“桥梁”作用。

例3：

如图(5)，⊙o₁与⊙o₂相交于A、B，CE切⊙o₁于C，交⊙o₂于D、E

求证：

分析：因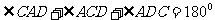，所以只需证

，联想到两圆相交时常添的辅助线，再运用弦切角定理及圆内接四边形性质，问题易得证。

　　 证：连结AB

　　　 CD切⊙o₁于C　

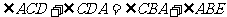
　　　 BEDA内接于⊙o₂

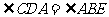
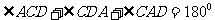
注意：如果⊙o₁的切线CE与⊙o₂也相切于E(D、E重合)，则

成立吗？

例4：如图(6)，⊙o₁与⊙o₂内切于A，过A作大圆的弦AD、AE分别交小圆于B、C。求证：

分析：要证，只需证，即要证BC∥DE；

证明：过点A作⊙o₁与⊙o₂的公切线AT，则：

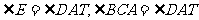
　　 ∵　　　 ∴BC∥DE

　　 ∴，即：

例5：如图(7)，⊙o₁与⊙o₂外切于A，BC分别切⊙o₁和⊙o₂于B、C，CA交⊙o₁于D，求证：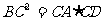

证明：过点A作⊙o₁、⊙o₂的公切线AE交BC于E，连结AB

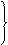
EB、EA为⊙o₁的切线EB＝EA　 EC＝EB＝EA

　　　　　　　　 同理：EC＝EA　　　　 　

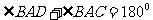
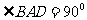
BD为⊙o₁的直径　 　

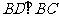
　　　　　　　　 BC为⊙o₁的切线　　 　

∽

注意：当两圆外切线内切时，公切线是常添的辅助线。

例6：如图(8)，两圆内切于点C，⊙o₁的弦AB切⊙o₂于E，CE的延长线交⊙o₁于点D，求证：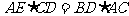

分析：要证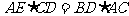

只须证，即要证∽，因两圆内切，所以可过点C作

公切线MN，从而证得：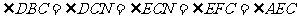

又因为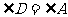，从而问题得以解决。

证明：过点C作⊙o₁与⊙o₂的公切线MN，连结EF、AC，

则有：

又∵AB为⊙o₂的切线，　　 ∴

　 ∴

又∵

　 ∴∽　　　 ∴

即：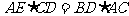

注：本讲内容较多，例题也比较详细、全面，因此不再单独设立练习题。

5、　 当两圆相交、外切、外离时，总有两条外公切线，且这两条外公切线长相等。如果两圆相等，那么两条外公切线平行；如果两圆不等，那么两条外公切线相交，且交点在两圆的连心线上。当两圆相切时，常作两圆的公切线为辅助线。

4、求两圆的内、外公切线长的问题，都是利用直线和圆相切的性质，通过作出过切点的半径，把问题转化为解一个直角三角形。

在图(2)、图(3)中，o₁o₂＝d，⊙o₁半径为R，⊙o₂的半径为r，则在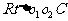中：

图(2)：

图(3)：

当两圆外切时，d＝R+r，此时

外公切线长＝

3、　 两圆的五种位置关系中，重点讨论了两圆相交、相切的性质，在解决两圆的相交问题时，如图(1)，常添连心线、公共弦等辅助线，这样，两圆半径、圆心距、公共弦长的一半就集中到了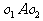中，可以利用三角形有关知识加以解决。