
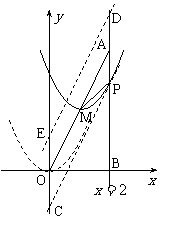
4、 (08浙江丽水)24.如图,在平面直角坐标系中,已知点
(08浙江丽水)24.如图,在平面直角坐标系中,已知点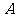 坐标为(2,4),直线
坐标为(2,4),直线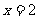 与
与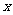 轴相交于点
轴相交于点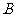 ,连结
,连结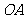 ,抛物线
,抛物线 从点
从点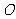 沿
沿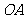 方向平移,与直线
方向平移,与直线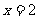 交于点
交于点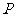 ,顶点
,顶点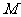 到
到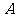 点时停止移动.
点时停止移动.
(1)求线段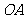 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点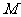 的横坐标为
的横坐标为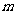 ,
,
①用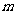 的代数式表示点
的代数式表示点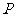 的坐标;
的坐标;
②当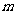 为何值时,线段
为何值时,线段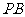 最短;
最短;
(3)当线段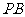 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点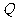 ,使△
,使△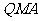
的面积与△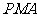 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点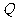 的坐标;若
的坐标;若
不存在,请说明理由.
(08浙江丽水24题解析)24.(本题14分)
解:(1)设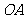 所在直线的函数解析式为
所在直线的函数解析式为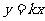 ,
,
∵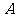 (2,4),
(2,4),
∴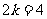 ,
, 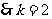 ,
,
∴ 所在直线的函数解析式为
所在直线的函数解析式为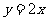 .…………………………………(3分)
.…………………………………(3分)
(2)①∵顶点M的横坐标为 ,且在线段
,且在线段 上移动,
上移动,
∴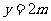 (0≤
(0≤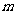 ≤2).∴顶点
≤2).∴顶点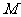 的坐标为(
的坐标为(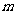 ,
,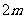 ).∴抛物线函数解析式为
).∴抛物线函数解析式为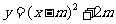 .
.
∴当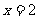 时,
时,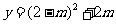
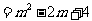 (0≤
(0≤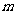 ≤2).
≤2).
∴点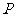 的坐标是(2,
的坐标是(2,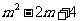 ).…………………………………(3分)
).…………………………………(3分)
② ∵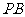 =
=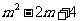 =
=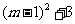 , 又∵0≤
, 又∵0≤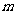 ≤2,
≤2,
∴当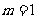 时,PB最短. ……………………………………………(3分)
时,PB最短. ……………………………………………(3分)
(3)当线段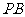 最短时,此时抛物线的解析式为
最短时,此时抛物线的解析式为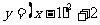 .……………(1分)
.……………(1分)
假设在抛物线上存在点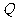 ,使
,使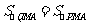 .
.
设点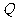 的坐标为(
的坐标为(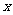 ,
,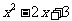 ).
).
①当点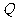 落在直线
落在直线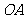 的下方时,过
的下方时,过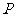 作直线
作直线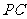 //
//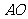 ,交
,交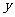 轴于点
轴于点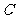 ,
,
∵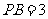 ,
,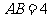 ,∴
,∴ ,∴
,∴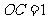 ,∴
,∴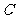 点的坐标是(0,
点的坐标是(0,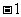 ).
).
 ∵点
∵点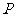 的坐标是(2,3),∴直线
的坐标是(2,3),∴直线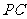 的函数解析式为
的函数解析式为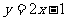 .
.
∵ ,∴点
,∴点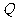 落在直线
落在直线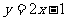 上.
上.
∴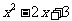 =
=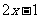 .
.
解得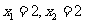 ,即点
,即点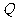 (2,3).
(2,3).
∴点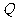 与点
与点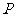 重合.
重合.
∴此时抛物线上不存在点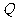 ,使△
,使△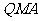 与
与
△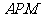 的面积相等.………………………(2分)
的面积相等.………………………(2分)
②当点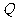 落在直线
落在直线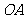 的上方时,作点
的上方时,作点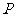 关于点
关于点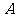 的对称称点
的对称称点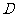 ,过
,过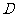 作直线
作直线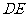 //
//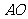 ,交
,交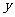 轴于点
轴于点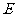 ,
,
∵ ,∴
,∴ ,∴
,∴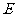 、
、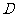 的坐标分别是(0,1),(2,5),
的坐标分别是(0,1),(2,5),
∴直线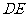 函数解析式为
函数解析式为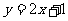 .
.
∵ ,∴点
,∴点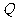 落在直线
落在直线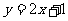 上.∴
上.∴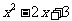 =
=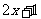 .
.
解得: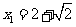 ,
,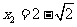 .代入
.代入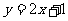 ,得
,得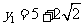 ,
, .
.
∴此时抛物线上存在点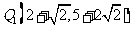 ,
,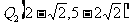
使△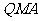 与△
与△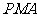 的面积相等. …………………………………(2分)
的面积相等. …………………………………(2分)
综上所述,抛物线上存在点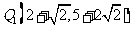 ,
,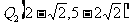
使△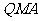 与△
与△ 的面积相等.
的面积相等.
3.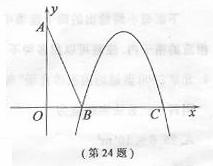 (08浙江杭州24) 在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数
(08浙江杭州24) 在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数 的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
(1)是否存在这样的抛物线F,使得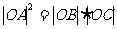 ?请你作出判断,并说明理由;
?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=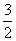 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。
(08浙江杭州24题解析)∵ 平移 的图象得到的抛物线
的图象得到的抛物线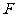 的顶点为
的顶点为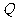 ,
,
∴ 抛物线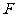 对应的解析式为:
对应的解析式为: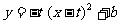 .
---
2分
.
---
2分
∵ 抛物线与x轴有两个交点,∴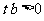 .
--- 1分
.
--- 1分
令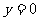 , 得
, 得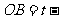
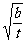 ,
,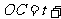
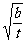 ,
,
∴ 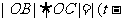
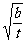 )(
)( 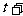
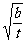 )|
)|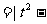
 ,
,
即 , 所以当
, 所以当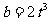 时, 存在抛物线
时, 存在抛物线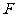 使得
使得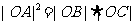 .-- 2分
.-- 2分
(2) ∵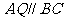 , ∴
, ∴ 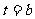 , 得
, 得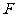 :
:  ,
,
解得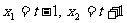 .
--- 1分
.
--- 1分
在
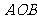 中,
中,
1) 当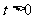 时,由
时,由 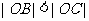 , 得
, 得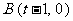 ,
,
当 时, 由
时, 由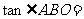
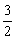
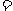
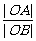
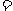
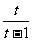 , 解得
, 解得 ,
,
此时, 二次函数解析式为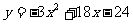 ;
--- 2分
;
--- 2分
当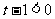 时, 由
时, 由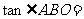
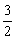
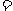
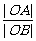
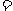
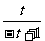 , 解得
, 解得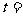
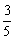 ,
,
此时,二次函数解析式为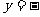
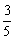
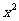 +
+
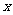 +
+ .
--- 2分
.
--- 2分
2) 当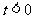 时, 由
时, 由 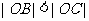 , 将
, 将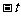 代
代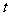 , 可得
, 可得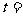
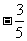 ,
, 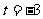 ,
,
(也可由 代
代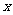 ,
,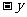 代
代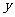 得到)
得到)
所以二次函数解析式为 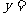
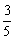
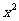 +
+
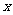 –
–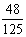 或
或 . --- 2分.
. --- 2分.
2. (08广东肇庆25题)(本小题满分10分)
已知点A(a,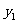 )、B(2a,y
)、B(2a,y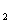 )、C(3a,y
)、C(3a,y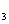 )都在抛物线
)都在抛物线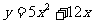 上.
上.
(1)求抛物线与x轴的交点坐标;(2)当a=1时,求△ABC的面积;
(3)是否存在含有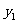 、y
、y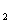 、y
、y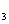 ,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
(08广东肇庆25题解析)(本小题满分10分)
解:(1)由5 =0,(1分)得
=0,(1分)得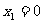 ,
,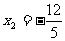 .(2分)∴抛物线与x轴的交点坐标为(0,0)、(
.(2分)∴抛物线与x轴的交点坐标为(0,0)、(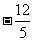 ,0). (3分)(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),·························· (4分)
,0). (3分)(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),·························· (4分)
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,则有
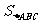 =S
=S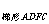 -
-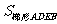 -
-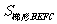 =
=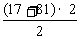 -
-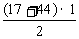 -
-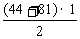 ······ =5(个单位面积)
······ =5(个单位面积)
(3)如: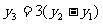 .事实上,
.事实上,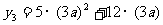 =45a2+36a.
=45a2+36a.
3( )=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.·············· (9分)
)=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.·············· (9分)
∴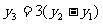 . ···················································································· (10分)
. ···················································································· (10分)
1.(08天津市卷26题)
已知抛物线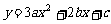 ,
,
(Ⅰ)若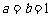 ,
, ,求该抛物线与
,求该抛物线与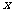 轴公共点的坐标;
轴公共点的坐标;
(Ⅱ)若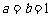 ,且当
,且当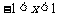 时,抛物线与
时,抛物线与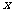 轴有且只有一个公共点,求
轴有且只有一个公共点,求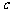 的取值范围;
的取值范围;
(Ⅲ)若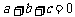 ,且
,且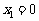 时,对应的
时,对应的 ;
; 时,对应的
时,对应的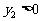 ,试判断当
,试判断当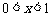 时,抛物线与
时,抛物线与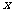 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
(08天津市卷26题解析)解(Ⅰ)当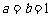 ,
, 时,抛物线为
时,抛物线为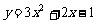 ,
,
方程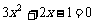 的两个根为
的两个根为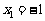 ,
,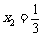 . ∴该抛物线与
. ∴该抛物线与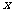 轴公共点的坐标是
轴公共点的坐标是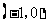 和
和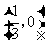 . 2分
. 2分
(Ⅱ)当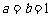 时,抛物线为
时,抛物线为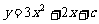 ,且与
,且与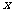 轴有公共点.
轴有公共点.
对于方程 ,判别式
,判别式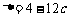 ≥0,有
≥0,有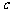 ≤
≤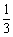 . ········································ 3分
. ········································ 3分
①当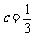 时,由方程
时,由方程 ,解得
,解得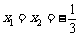 .
.
此时抛物线为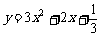 与
与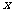 轴只有一个公共点
轴只有一个公共点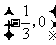 .·································
4分
.·································
4分
②当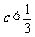 时,
时, 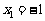 时,
时,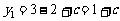 ,
, 时,
时,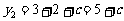 .
.
由已知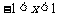 时,该抛物线与
时,该抛物线与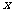 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为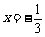 ,
,
应有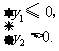 即
即 解得
解得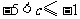 .
.
综上,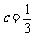 或
或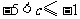 . ················································································ 6分
. ················································································ 6分
(Ⅲ)对于二次函数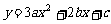 ,
,
由已知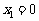 时,
时, ;
; 时,
时, ,
,
又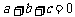 ,∴
,∴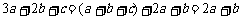 .
.
于是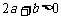 .而
.而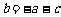 ,∴
,∴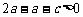 ,即
,即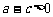 .∴
.∴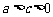 . 7分
. 7分
∵关于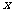 的一元二次方程
的一元二次方程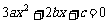 的判别式
的判别式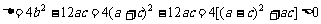 ,
,
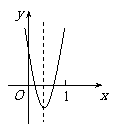 ∴抛物线
∴抛物线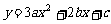 与
与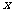 轴有两个公共点,顶点在
轴有两个公共点,顶点在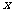 轴下方.····························· 8分
轴下方.····························· 8分
又该抛物线的对称轴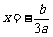 ,
,
由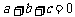 ,
,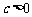 ,
,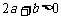 ,
,
得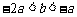 ,
,
∴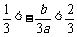 .
.
又由已知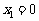 时,
时, ;
; 时,
时,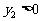 ,观察图象,
,观察图象,
可知在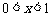 范围内,该抛物线与
范围内,该抛物线与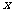 轴有两个公共点. ············································ 10分
轴有两个公共点. ············································ 10分
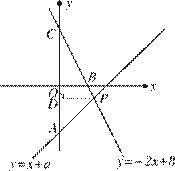
28、(10分)如图,直线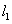 的解析表达式为
的解析表达式为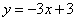 ,且
,且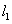 与
与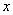 轴交于点
轴交于点 ,直线
,直线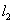 经过点
经过点 ,直线
,直线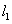 ,
,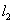 交于点
交于点 .
.
(1)求点 的坐标;
的坐标;
(2)求直线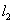 的解析表达式;
的解析表达式;
(3)求 的面积;
的面积;
(4)在直线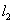 上存在异于点
上存在异于点 的另一点
的另一点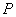 ,使得
,使得
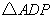 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点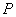 的坐标.
的坐标.
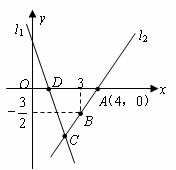
5.00元/升,问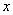 为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费);
为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费);
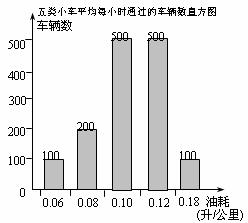
(3)据杭州湾跨海大桥管理部门统计:从宁波经跨 海大桥到上海的小车中,其中五类不同油耗的小车平均每小时通过的车辆数,得到如图所示的频数分布直方图,请你估算1天内这五类小车走直路比走弯路共节省多少升汽油.
27、(10分)为了促进长三角区域的便捷沟通,实现节时、节能,杭州湾跨海大桥于今年5月1日通车,下表是宁波到上海两条线路的有关数据:
|
线路 |
弯路(宁波-杭州-上海) |
直路(宁波-跨海大桥-上海) |
|
路程 |
316公里 |
196公里 |
|
过路费 |
140元 |
180元 |
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为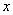 升,汽油价格为
升,汽油价格为
26、(10分)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、
H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
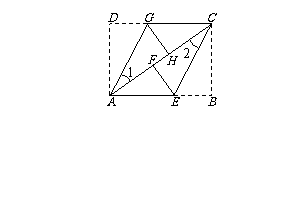 (2)若AB=4cm,BC=3cm,求线段EF的长.
(2)若AB=4cm,BC=3cm,求线段EF的长.
图6
25、(10分)已知直线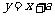 与
与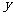 轴的负半轴交于点
轴的负半轴交于点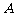 ,直线
,直线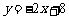 与
与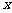 轴交于点
轴交于点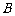 ,与
,与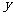 轴交于点
轴交于点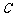 ,
,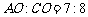 (
( 是坐标原点),两条直线交于点
是坐标原点),两条直线交于点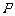 .
.
(1)求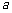 的值及点
的值及点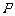 的坐标;
的坐标;
(2)求四边形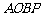 的面积
的面积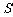 .
.
24、(10分)2008年8月8日,第29届奥运会将在北京举行.现在,奥运会门票已在世界各地开始销售,下图是奥运会部分项目的门票价格:

(1)从以上统计图可知,同一项目门票价格相差很大,分别求出篮球项目门票价格的极差和跳水项目门票价格的极差.
(2)求出这6个奥运会项目门票最高价的平均数、中位数和众数.
(3)田径比赛将在国家体育场“鸟巢”进行,“鸟巢”内共有观众座位9.1万个.从安全角度考虑,正式比赛时将留出0.6万个座位.某场田径赛,组委会决定向奥运赞助商和相关部门赠送还1.5万张门票,其余门票全部售出.若售出的门票中最高价门票占10%至15%,其他门票的平均价格是300元,你估计这场比赛售出的门票收入约是多少万元?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com