
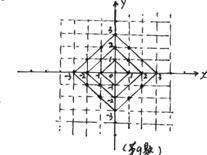
9. 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有 个。
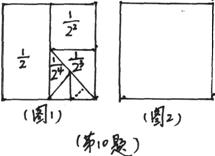
8. 用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子 枚(用含有n的代数式表示)。
○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
○ ● ● ○ ○ ● ● ● ○
○ ● ○ ○ ● ● ○ ○ ● ● ● ○
○ ○ ○ ○ ○ ● ● ● ○
○ ○ ○ ○ ○ ○ ○ ○
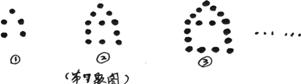
7. 如图,摆第1个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第3个要17枚棋子,则摆第30个“小屋子”要 枚棋子。
6. 已知n(n≥2)个点P1、P2、P3…Pn在同一平面内,且其中没有任何三点在同一直线上,设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然S2=1,S3=3,S4=6,S5=10…,由此推断Sn= 。
5. 将正奇数如下表排列:
按表中的排列规则,数
2005应排在第 行第 列。
4. 观察下面一列数: 1
-2 3 -4
5 -6 7 -8 9
-10 11 -12 13 -14 15 -16
…… ……
按上述规律排下去,那么第10行从左边数第9个数是 。
 列 列行 |
一 |
二 |
三 |
四 |
五 |
|
一 |
|
1 |
3 |
5 |
7 |
|
二 |
15 |
13 |
11 |
9 |
|
|
三 |
|
17 |
19 |
21 |
23 |
|
四 |
… |
… |
27 |
25 |
|
3. 下列是一个有规律排列的数表:
第1列 第2列 第3列 第4列…第n例…
第1行: 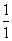
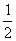
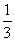
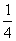 …
…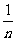 …
…
第2行: 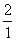
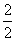
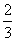
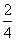 …
…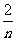 …
…
第3行: 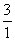
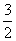
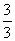
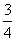 …
…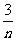 …
…
上面数表中第9行,第7列的数是
2. 瑞士中学教师巴尔米成功地从光谱数据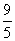 、
、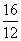 、
、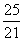 、
、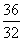 …中得到巴尔
…中得到巴尔
米公式,从而打开了光谱奥妙的大门,请你按这种规律写出第七个数 。
1. 观察:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256…
通过观察用你所发现的规律写出22008的未位数是 。
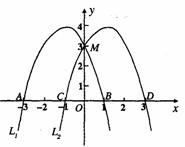
5、(2008山东烟台)如图,抛物线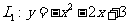 交
交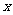 轴于A、B两点,交
轴于A、B两点,交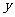 轴于M点.抛物线
轴于M点.抛物线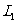 向右平移2个单位后得到抛物线
向右平移2个单位后得到抛物线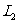 ,
,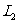 交
交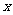 轴于C、D两点.
轴于C、D两点.
(1)求抛物线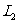 对应的函数表达式;
对应的函数表达式;
(2)抛物线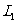 或
或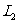 在
在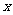 轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
(3)若点P是抛物线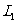 上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线
上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线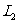 上,请说明理由.
上,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com