
6.(2008湖北鄂州)下列方程中,有两个不等实数根的是( )
A.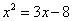 B.
B.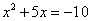
C.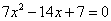 D.
D.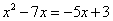
答案:D
5.(2008湖北黄石)已知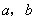 是关于
是关于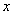 的一元二次方程
的一元二次方程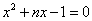 的两实数根,则式子
的两实数根,则式子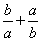 的值是( )
的值是( )
A.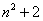 B.
B.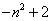 C.
C.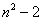 D.
D.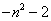
答案:D
4.(2008年江苏省南通市)设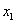 、
、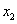 是关于x的一元二次方程
是关于x的一元二次方程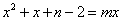 的两个实数根,且
的两个实数根,且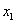 <0,
<0,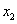 -3
-3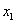 <0,则(
)
<0,则(
)
A.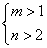 B.
B.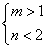 C.
C.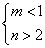 D.
D.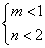
答案:B
3.(2008年大庆市)已知关于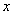 的一元二次方程
的一元二次方程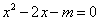 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数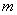 的取值范围是( )
的取值范围是( )
A. B.
B.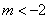 C.
C.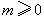 D.
D.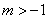
答案:D
2.(2008年山东省潍坊市)已知反比例函数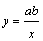 ,当x>0时,y随x的增大而增大,则关于x的方程
,当x>0时,y随x的增大而增大,则关于x的方程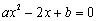 的根的情况是( )
的根的情况是( )
A.有两个正根 B.有两个负根 C.有一个正根一个负根 D.没有实数根
答案:C
1.(2008山东威海)关于x的一元二次方程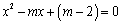 的根的情况是
的根的情况是
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
答案:A
8、(四川自贡)抛物线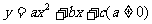 的顶点为M,与
的顶点为M,与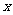 轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b.若关
轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b.若关
于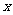 的一元二次方程
的一元二次方程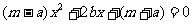 有两个相等的实数根.
有两个相等的实数根.
(1)判断△ABM的形状,并说明理由.
(2)当顶点M的坐标为(-2,-1)时,求抛物线的解析式,并画出该抛物线的大
致图形.
(3)若平行于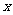 轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与
轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与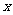 轴相切,
轴相切,
求该圆的圆心坐标.
(1)令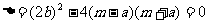 ,得
,得
由勾股定理的逆定理和抛物线的对称性知△ABM是一个以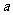 、
、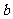 为直角边的等腰直角三角形
为直角边的等腰直角三角形
 (2)设
(2)设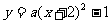
∵△ABM是等腰直角三角形
∴斜边上的中线等于斜边的一半
|
|
|
|
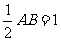 ,即AB=2
,即AB=2
∴A(-3,0),B(-1,0)
将B(-1,0) 代入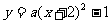 中得
中得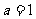
∴抛物线的解析式为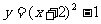 ,即
,即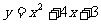
(3)设平行于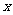 轴的直线为
轴的直线为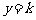
解方程组
得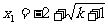 ,
, (
(
∴线段CD的长为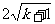
∵以CD为直径的圆与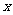 轴相切
轴相切
据题意得
∴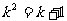
解得 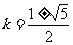
∴圆心坐标为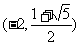 和
和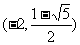
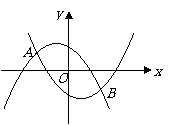
7、(江西省)已知:如图所示的两条抛物线的解析式分别是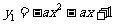 ,
,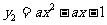 (其中
(其中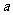 为常数,且
为常数,且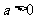 ).
).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当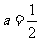 时,设
时,设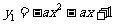 与
与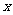 轴分别交于
轴分别交于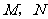 两点(
两点(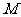 在
在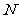 的左边),
的左边),
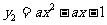 与
与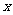 轴分别交于
轴分别交于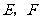 两点(
两点(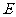 在
在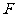 的左边),观察
的左边),观察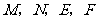 四点坐标,请写出一个你所得到的正确结论,并说明理由;
四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于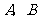 两点,直线
两点,直线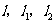 都垂直于
都垂直于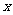 轴,
轴,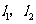 分别经过
分别经过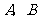 两点,
两点,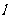 在直线
在直线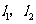 之间,且
之间,且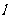 与两条抛物线分别交于
与两条抛物线分别交于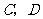 两点,求线段
两点,求线段 的最大值.
的最大值.
(1)解:答案不唯一,只要合理均可.例如:
①抛物线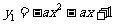 开口向下,或抛物线
开口向下,或抛物线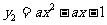 开口向上;
开口向上;
②抛物线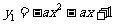 的对称轴是
的对称轴是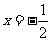 ,或抛物线
,或抛物线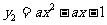 的对称轴是
的对称轴是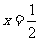 ;
;
③抛物线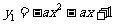 经过点
经过点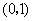 ,或抛物线
,或抛物线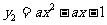 经过点
经过点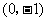 ;
;
④抛物线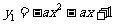 与
与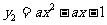 的形状相同,但开口方向相反;
的形状相同,但开口方向相反;
⑤抛物线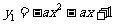 与
与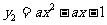 都与
都与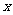 轴有两个交点;
轴有两个交点;
⑥抛物线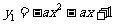 经过点
经过点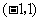 或抛物线
或抛物线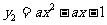 经过点
经过点 ;
;
等等.
(2)当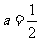 时,
时,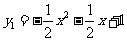 ,令
,令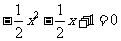 ,
,
解得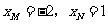 .
.
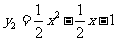 ,令
,令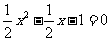 ,解得
,解得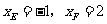 .
.
①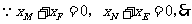 点
点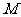 与点
与点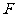 对称,点
对称,点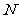 与点
与点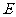 对称;
对称;
②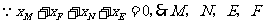 四点横坐标的代数和为0;
四点横坐标的代数和为0;
③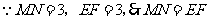 (或
(或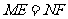 ).
).
(3)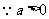 ,
,
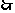 抛物线
抛物线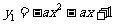 开口向下,抛物线
开口向下,抛物线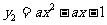 开口向上.
开口向上.
根据题意,得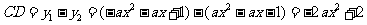 .
.
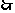 当
当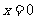 时,
时, 的最大值是2.
的最大值是2.
6、(广西南宁)随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润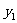 与投资量
与投资量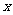 成正比例关系,如图①所示;种植花卉的利润
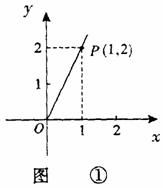
成正比例关系,如图①所示;种植花卉的利润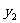 与投资量
与投资量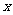 成二次函数关系,如图②所示(注:利润与投资量的单位:万元)
成二次函数关系,如图②所示(注:利润与投资量的单位:万元)
(1)分别求出利润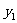 与
与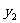 关于投资量
关于投资量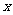 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
解:(1)设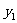 =
=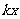 ,由图①所示,函数
,由图①所示,函数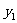 =
=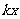 的图像过(1,2),所以2=
的图像过(1,2),所以2=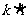 ,
,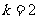
故利润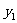 关于投资量
关于投资量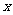 的函数关系式是
的函数关系式是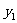 =
=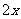 ;
;
因为该抛物线的顶点是原点,所以设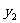 =
=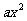 ,由图12-②所示,函数
,由图12-②所示,函数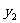 =
=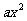 的图像过(2,2),
的图像过(2,2),
所以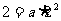 ,
,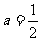
故利润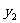 关于投资量
关于投资量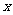 的函数关系式是
的函数关系式是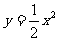 ;
;
(2)设这位专业户投入种植花卉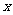 万元(
万元(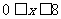 ),
),
则投入种植树木(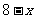 )万元,他获得的利润是
)万元,他获得的利润是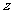 万元,根据题意,得
万元,根据题意,得
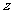 =
=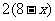 +
+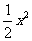 =
=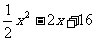 =
=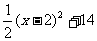
当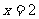 时,
时,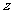 的最小值是14;
的最小值是14;
因为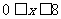 ,所以
,所以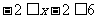
 所以
所以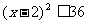
所以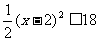
所以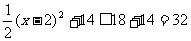 ,即
,即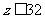 ,此时
,此时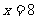
当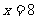 时,
时,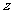 的最大值是32.
的最大值是32.
5、(吉林长春)已知两个关于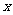 的二次函数
的二次函数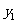 与当
与当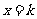 时,
时,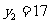 ;且二次函数
;且二次函数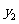 的图象的对称轴是直线
的图象的对称轴是直线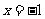 .
.

(1)求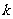 的值;
的值;
(2)求函数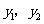 的表达式;
的表达式;
(3)在同一直角坐标系内,问函数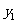 的图象与
的图象与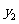 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.
解:(1)由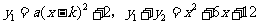
得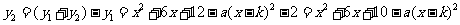 .
.
又因为当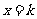 时,
时,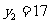 ,即
,即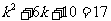 ,
,
解得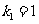 ,或
,或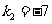 (舍去),故
(舍去),故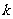 的值为
的值为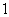 .
.
(2)由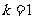 ,得
,得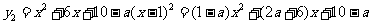 ,
,
所以函数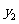 的图象的对称轴为
的图象的对称轴为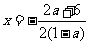 ,
,
于是,有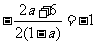 ,解得
,解得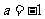 ,
,
所以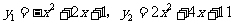 .
.
(3)由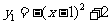 ,得函数
,得函数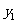 的图象为抛物线,其开口向下,顶点坐标为
的图象为抛物线,其开口向下,顶点坐标为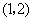 ;
;
由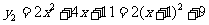 ,得函数
,得函数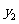 的图象为抛物线,其开口向上,顶点坐标为
的图象为抛物线,其开口向上,顶点坐标为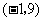 ;
;
故在同一直角坐标系内,函数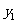 的图象与
的图象与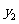 的图象没有交点.
的图象没有交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com