
10.(33)(.2008 江西)一个几何体是由一些大小相同的小正方块摆成的,其俯视图
与主视图如图所示,则组成这个几何体的小正方块最多有( C )
A.4个 B.5个 C.6个 D.7个
(34)(08厦门市)由四个相同的小正方体堆成的物体如图所示,它的俯视图是( C )

(35)(08乌兰察布市)六个大小相同的正方体搭成的几何体如图所示,则关于它的
视图说法正确的是( C )

A.正视图的面积最大
B.左视图的面积最大
C.俯视图的面积最大
D.三个视图的面积一样大
(36)(08莆田市)如图,茶杯的主视图是 ( A )

(37)(08绵阳市)某几何体的三视图如下所示,则该几何体可以是( A ).

(38)(2008年杭州市)由大小相同的正方体木块堆成的几何体的三视图如右图所示,则该几何体中正方体木块的个数是( C )

A. 6个 B. 5个
C. 4个 D. 3个
(39)(2008泰安)如图是由相同小正方体组成的立体图形,它的左视图为( A )

 (40)(2008佛山)如图,是某工件的三视图,其中圆的半径为10
(40)(2008佛山)如图,是某工件的三视图,其中圆的半径为10 ,等腰三角形的高为30
,等腰三角形的高为30 ,则此工件的侧面积是(
D )
,则此工件的侧面积是(
D ) .
.
A.
B.
C.
D.
(41)(2008 山东 聊城)一个几何体的三视图如图所示,这个几何体是( B )
A.棱柱 B.圆柱 C.圆锥 D.球

(42)(2008四川内江)在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有( D )
A.9箱 B.10箱 C.11箱 D.12箱

(43)(2008泰州市)如左下图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为(A)
A. 2cm3 B.4 cm3 C.6 cm3 D.8 cm3

(44)(2008山西省)如图,有一圆心角为120 o、半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是(A)
A. cm
cm
B. cm
cm
C. cm
cm
D. cm
cm

(45).(2008永州市)下图※是一种瑶族长鼓的轮廓图,其主视图正确的是( D )

(46)(2008四川达州市)某几何体的三视图如图所示,则它是( D )
A.球体 B.圆柱 C.棱锥 D.圆锥

(47)(2008广东深圳)如图1,圆柱的左视图是 ( C )

(48)(2008山西太原)右图是一个正方体的平面展开图,这个正方体是( D )

(49)(2008湖北武汉)一个无盖的正方体盒子的平面展开图可以是下列图形中的( D ).

(50)(2008湖北孝感)一几何体的三视图如右,这个几何体是( D )
A.圆锥 B.圆柱 C. 三棱锥 D. 三棱柱

(51)(2008湖北襄樊)如图5,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( C )

(52)(2008江苏盐城)下列四个几何体中,主视图、左视图、俯视图完全相同的是( B )
A.圆锥 B.球 C.圆柱 D.三棱柱
(53)(2008湖北黄冈)如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是( C )
A.长方体 B.圆柱体 C.球体 D.三棱柱

(54)(2008黑龙江哈尔滨)4.右图是某一几何体的三视图,则这个几何体是( A )。
(A)圆柱体 (B)圆锥体
(C)正方体 (D)球体

(55)(2008福建省泉州市)右边物体的左视图是( D )

(56)(2008年湖南邵阳市)如图(一),直角梯形 中,
中, ,
, .将直角梯形
.将直角梯形 绕边
绕边 旋转一周,所得几何体的俯视图是( D )
旋转一周,所得几何体的俯视图是( D )

(57)(2008年四川省南充市)如图,下列选项中不是正六棱柱三视图的是( A )

(58)(2008年浙江省衢州)下面形状的四张纸板,按图中线经过折叠可以围成一下直三棱柱的是( C )

(59)(2008年山东省威海市)下图的几何体是由三个同样大小的立方体搭成的,其左视图为 (A)

(60).(2008山东济宁)如图,是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是( B )

(61)(2008江苏淮安)如图所示的几何体的俯视图是( D )

(62)(2008湖北宜昌市)下列物体的形状类似于球的是( C)
A.茶杯 B.羽毛球 C.乒乓球 D.白炽灯泡
(63)(2008湖北宜昌市)如图是江峡中学实验室某器材的主视图和俯视图,那么这个器材可能是( A )

A.条形磁铁 B.天平砝码 C.漏斗 D.试管
(64)(2008桂林市)右图是由四个相同的小立方体组成的立体图形,它的左视图是(C )

(65) (2008黑龙江黑河)下列各图中,不是正方体展开图的是( C )

(66)(2008广州市)下面四个图形中,是三棱柱的平面展开图的是( A )

(67)(2008广东肇庆市)一个正方体的面共有( D )
A.1个 B.2个 C.4个 D.6个
(68)(2008广东肇庆市)如图2,箭头表示投影线的方向,则图中圆柱体的正投影是( D )
A.圆 B.圆柱 C.梯形 D.矩形

(69)(08山东省日照市)如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是  .
.

(70)(2008年辽宁省十二市)一个圆锥底面周长为 cm,母线长为5cm,则这个圆锥的侧面积是
cm,母线长为5cm,则这个圆锥的侧面积是 (丢单位扣1分)
(丢单位扣1分)
(71)(2008年乐山市)图(8)是一个几何体的三视图,根据图示,可计算出该几何体的侧面积为:8

(72)((2008年大庆市)如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形 ,点
,点 是母线
是母线 的中点,一只蚂蚁从点
的中点,一只蚂蚁从点 出发沿圆锥的表面爬行到点
出发沿圆锥的表面爬行到点 处,则这只蚂蚁爬行的最短距离是
处,则这只蚂蚁爬行的最短距离是 cm.
cm.
(73)(2008浙江湖州)一个长、宽、高分别为15cm、10cm、5cm的长方体包装盒的表面积为550cm2 .
(73)(2008年江苏省南通市)一个长方体的主视图和左视图如图所示(单位:cm),则俯视图的面积是6cm2.

(74)(2008年江苏省苏州市)如图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 24 .

(75)(2008年浙江嘉兴)一个几何体的三视图如图所示,则这个几何体的名称是直棱柱.

(76)(2008 湖北恩施) 如图,该图形经过折叠可以围成一个正方体形,折好以后,与“静”字相对的字是 着 .

(77)(2008宁夏)制作一个圆锥模型,已知圆锥底面圆的半径为3.5cm,侧面母线长为6cm,则此圆锥侧面展开图的扇形圆心角为 210 度.
(78)(2008宁夏)展览厅内要用相同的正方体木块搭成一个三视图如右图的展台,则此展台共需这样的正方体10块.

9. (2008年广东梅州市)本题满分8分.
已知关于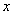 的一元二次方程
的一元二次方程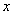 2-
2-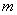
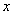 -2=0………①.
-2=0………①.
(1) 若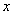 =-1是这个方程的一个根,求
=-1是这个方程的一个根,求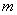 的值和方程①的另一根;
的值和方程①的另一根;
(2) 对于任意的实数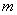 ,判断方程①的根的情况,并说明理由.
,判断方程①的根的情况,并说明理由.
解:(1) 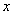 =-1是方程①的一个根,所以1+
=-1是方程①的一个根,所以1+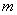 -2=0, ······· 1分
-2=0, ······· 1分
解得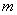 =1. ······················· 2分
=1. ······················· 2分
方程为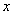 2-
2-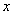 -2=0, 解得,
-2=0, 解得, 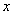 1=-1,
1=-1, 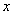 2=2.
2=2.
所以方程的另一根为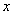 =2.················· 4分
=2.················· 4分
(2)  =
=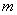 2+8,··················· 5分
2+8,··················· 5分
因为对于任意实数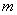 ,
,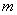 2≥0,··············· 6分
2≥0,··············· 6分
所以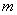 2+8>0,······················· 7分
2+8>0,······················· 7分
所以对于任意的实数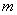 ,方程①有两个不相等的实数根. ···· 8分
,方程①有两个不相等的实数根. ···· 8分
8. (2008广东中山)已知关于x的方程 .
.
(1)求证方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
解:(1)证明:因为△= ……1分
……1分
= ……3分
……3分
所以无论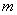 取何值时, △>0,所以方程有两个不相等的实数根。
取何值时, △>0,所以方程有两个不相等的实数根。
(2)解:因为方程的两根互为相反数,所以 ,……5分
,……5分
根据方程的根与系数的关系得 ,解得
,解得 ,……7分
,……7分
所以原方程可化为 ,解得
,解得 ,
, ……9分
……9分
7. (2008甘肃兰州)已知关于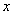 的一元二次方程
的一元二次方程 .
.
(1)如果此方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)如果此方程的两个实数根为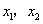 ,且满足
,且满足 ,求
,求 的值.
的值.
解:(1) .··············· 1分
.··············· 1分
 方程有两个不相等的实数根,
方程有两个不相等的实数根, .··············· 2分
.··············· 2分
即 .···························· 3分
.···························· 3分
(2)由题意得: ,
, .··············· 4分
.··············· 4分

 ,
,
 .··························· 6分
.··························· 6分
 . 7分
. 7分
6.(2008湖北孝感)已知关于x的一元二次方程 有两个实数根
有两个实数根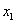 和
和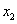 。
。
(1)求实数m的取值范围;
(2)当 时,求m的值。
时,求m的值。
(友情提示:若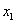 、
、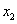 是一元二次方程
是一元二次方程 两根,则有
两根,则有 ,
, )
)
解:(1)由题意有 ,解得
,解得 ,即实数m的取值范围是
,即实数m的取值范围是 。
。
(2)由 。
。
若 ,即-(2m-1)=0,解得
,即-(2m-1)=0,解得 ,
,
 不合题意,舍去。
不合题意,舍去。
若
 ,由(1)知
,由(1)知 。故当
。故当 。
。
5. (2008 河南实验区)已知
 是关于
是关于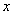 的一元二次方程
的一元二次方程 的两个实数根,且
的两个实数根,且
 -
- -
- =115
=115
(1)求k的值;(2)求 +
+ +8的值。
+8的值。
解:(1)∵x ,x
,x 是方程x
是方程x -6x+k=0的两个根
-6x+k=0的两个根
∴x + x
+ x =6
x
=6
x x
x =k
=k
∵
 -
- -
- =115
=115
∴k -6=115
-6=115
解得k =11,k
=11,k =-11
=-11
当k =11时
=11时 =36-4k=36-44<0 ,∴k
=36-4k=36-44<0 ,∴k =11不合题意
=11不合题意
当k =-11时
=-11时 =36-4k=36+44>0∴k
=36-4k=36+44>0∴k =-11符合题意
=-11符合题意
∴k的值为-11
(2)x +x
+x =6,x
=6,x x
x =-11
=-11
而x
 +x
+x
 +8=(x
+8=(x +x
+x )
) -2x
-2x x
x +8=36+2×11+8=66
+8=36+2×11+8=66
4. (2008 广东)(1)解方程求出两个解 、
、 ,并计算两个解的和与积,填人下表
,并计算两个解的和与积,填人下表

(2)观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律?写出你的结论.
解:(1)  ,
,  , 0,
, 0,  ;
;
 , 0,
, 0,  , 0;
, 0;
2, 1, 3, 2;
 ,
,  .
.
(2)已知: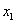 和
和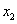 是方程
是方程 的两个根,
的两个根,
那么, ,
,  .
.
3.(2008北京)已知:关于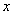 的一元二次方程
的一元二次方程 .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为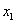 ,
,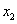 (其中
(其中 ).若
).若 是关于
是关于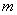 的函数,且
的函数,且 ,求这个函数的解析式;
,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量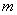 的取值范围满足什么条件时,
的取值范围满足什么条件时, .
.
解:(1)证明: 是关于
是关于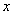 的一元二次方程,
的一元二次方程,
 .
.
 当
当 时,
时, ,即
,即 .
. 方程有两个不相等的实数根.
方程有两个不相等的实数根.
(2)解:由求根公式,得 .
. 或
或 .
.
 ,
, .
. ,
, ,
, .
.
 .即
.即 为所求.
为所求.
(3)解:在同一平面直角坐标系中分别画出
 与
与 的图象.
的图象.
由图象可得,当 时,
时, .
.

2.(2008湖北鄂州)设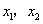 是关于
是关于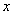 的一元二次方程
的一元二次方程 的两实根,当
的两实根,当 为何值时,
为何值时, 有最小值?最小值是多少?
有最小值?最小值是多少?
解答:
 又
又 ,
,



 当
当 时,
时, 的值最小
的值最小
此时 ,即最小值为
,即最小值为 .
.
1.(2008 湖南 长沙)当 为何值时,关于
为何值时,关于 的一元二次方程
的一元二次方程 有两个相等的实数根?此时这两个实数根是多少?
有两个相等的实数根?此时这两个实数根是多少?
解:由题意,△=(-4)2-4(m- )=0
)=0
即16-4m+2=0,m= .
.
当m= 时,方程有两个相等的实数根x1=x2=2.
时,方程有两个相等的实数根x1=x2=2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com