
7. (2008黑龙江哈尔滨)荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
解:(1)设租用一辆甲型汽车的费用是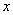 元,租用一辆乙型汽车的费用是
元,租用一辆乙型汽车的费用是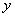 元.
元.
由题意得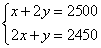 ··························· 2分
··························· 2分
解得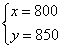 ······························· 1分
······························· 1分
答:租用一辆甲型汽车的费用是800元,租用一辆乙型汽车的费用是850元.
(2)设租用甲型汽车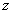 辆,则租用乙型汽车
辆,则租用乙型汽车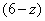 辆.
辆.
由题意得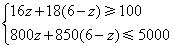 ····················· 2分
····················· 2分
解得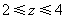 ······························· 1分
······························· 1分
由题意知,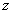 为整数,
为整数,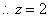 或
或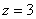 或
或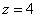
 共有3种方案,分别是:
共有3种方案,分别是:
方案一:租用甲型汽车2辆,租用乙型汽车4辆;
方案二:租用甲型汽车3辆,租用乙型汽车3辆;
方案三:租用甲型汽车4辆,租用乙型汽车2辆.················ 1分
方案一的费用是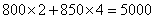 (元);
(元);
方案二的费用是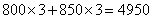 (元);
(元);
方案三的费用是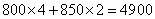 (元)
(元)
 ,所以最低运费是4900元.················ 1分
,所以最低运费是4900元.················ 1分
答:共有3种方案,分别是:方案一:租用甲型汽车2辆,租用乙型汽车4辆;
方案二:租用甲型汽车3辆,租用乙型汽车3辆;
方案三:租用甲型汽车4辆,租用乙型汽车2辆.
最低运费是4900元.
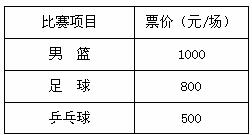
6.(2008湖南株洲)22.2008年北京奥运会的比赛门票开始接受公众预定.下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格,某球迷准备用12000元预定15张下表中球类比赛的门票:
(1)若全部资金用来预定男篮门票和乒乓球门票,问这个球迷可以预订男篮门票和乒乓球门票各多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,问可以预订这三种球类门票各多少张?
解:(1)设预定男篮门票x张,则乒乓球门票(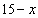 )张.得:1000x+500(15-x)=12000,解得:x = 9 ∴
)张.得:1000x+500(15-x)=12000,解得:x = 9 ∴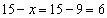
(2)设足球门票与乒乓球门票数都预定y张,则男篮门票数为(15-2y)张,得: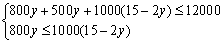 ,
,
解得: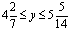 .由y为正整数可得y=5. 15-2y=5
.由y为正整数可得y=5. 15-2y=5
答:(1)略 (2)略
5.(2008年山东省潍坊市)为了美化校园环境,建设绿色校园,某学校准备对校园中30亩空地进行绿化..绿化采用种植草皮与种植树木两种方式,要求种植草皮与种植树木的面积都不少于10亩,并且种植草皮面积不少于种植树木面积的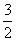 .已知种植草皮与种植树木每亩的费用分别为8000元与12000元.
.已知种植草皮与种植树木每亩的费用分别为8000元与12000元.
(1) 种植草皮的最小面积是多少?
种植草皮的面积为多少时绿化总费用最低?最低费用为多少
解:(1)解设种植草皮的面积为x亩,则种植树木面积为(30-x)亩,则:
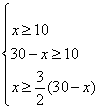 解得
解得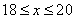
答:种植草皮的最小面积是18亩。
(2)由题意得:y=8000x+12000(30-x)=360000-4000x,当x=20时y有最小值280000元
4.(2008湖南益阳)乘坐益阳市某种出租汽车.当行驶路程小于2千米时,乘车费用都是4元(即起步价4元);当行驶路程大于或等于2千米时,超过2千米部分每千米收费1.5元.
(1)请你求出x≥2时乘车费用y(元)与行驶路程x(千米)之间的函数关系式;
(2)按常规,乘车付费时按计费器上显示的金额进行“四舍五入”后取整(如记费器上的数字显示范围大于或等于9.5而小于10.5时,应付车费10元),小红一次乘车后付了车费8元,请你确定小红这次乘车路程x的范围.
解:(1) 根据题意可知:y=4+1.5(x-2) ,
∴ y=1.5x+1(x≥2) ················· 4分
(2)依题意得:7.5≤1.5x+1<8.5 ··················· 6分
∴ 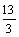 ≤x<5····················· 8分
≤x<5····················· 8分
3.(08浙江温州)一次奥运知识竞赛中,一共有25道题,答对一题得10分,答错(或不答)一题扣5分.设小明同学在这次竞赛中答对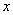 道题.
道题.
(1)根据所给条件,完成下表:
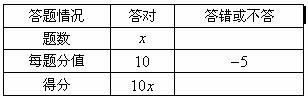
(2)若小明同学的竞赛成绩超过100分,则他至少答对几道题?
解:(1)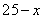 ;
;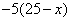
(2)根据题意,得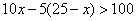
解得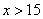
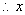 的最小正整数解是
的最小正整数解是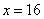
答:小明同学至少答对16道题
2.(2008年浙江省衢州市)1月底,某公司还有11000千克椪柑库存,这些椪柑的销售期最多还有60天,60天后库存的椪柑不能再销售,需要当垃圾处理,处理费为0.05元/吨。经测算,椪柑的销售价格定为2元/千克时,平均每天可售出100千克,销售价格降低,销售量可增加,每降低0.1元/千克,每天可多售出50千克。
(1)如果按2元/千克的价格销售,能否在60天内售完这些椪柑?按此价格销售,获得的总毛利润是多少元(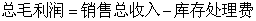 )?
)?
(2)设椪柑销售价格定为x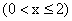 元/千克时,平均每天能售出y千克,求y关于x的函数解析式;如果要在2月份售完这些椪柑(2月份按28天计算),那么销售价格最高可定为多少元/千克(精确到0.1元/千克)?
元/千克时,平均每天能售出y千克,求y关于x的函数解析式;如果要在2月份售完这些椪柑(2月份按28天计算),那么销售价格最高可定为多少元/千克(精确到0.1元/千克)?
解:(1)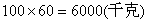 ,所以不能在60天内售完这些椪柑,
,所以不能在60天内售完这些椪柑,
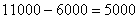 (千克)
(千克)
即60天后还有库存5000千克,总毛利润为
W=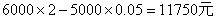 ;
;
(2)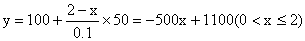
要在2月份售完这些椪柑,售价x必须满足不等式
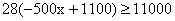
解得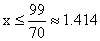
所以要在2月份售完这些椪柑,销售价最高可定为1.4元/千克。
1.(2008年四川省宜宾市)某学校准备添置一些“中国结”挂在教室。若到商店去批量购买,每个“中国结”需要10元;若组织一些同学自己制作,每个“中国结”的成本是4元,无论制作多少,另外还需共付场地租金200元。亲爱的同学,请你帮该学校出个主意,用哪种方式添置“中国结”的费用较节省?
解:设需要中国结x个,则直接购买需4x+200元,自制需10x元
分两种情况:
(1)若10x<4x+200,得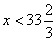 ,即少于33个时,到商店购买更便宜
,即少于33个时,到商店购买更便宜
(2)若10x>4x+200,得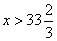 即少于33个时,自已制作更便宜.
即少于33个时,自已制作更便宜.
3.(2008齐齐哈尔)为紧急安置100名地震灾民,需要同时搭建可容纳6人和4人的两种帐篷,则搭建方案共有( )
A.8种 B.9种 C.16种 D.17种
答案:A
2.(2008 台湾)某段隧道全长9公里,有一辆汽车以每小时60公里到80公里之间的速率通过该隧道。下列何者可能是该车通过隧道所用的时间?( ) (A) 6分钟 (B) 8分钟 (C) 10分钟 (D) 12分钟
答案:B
1.(08厦门市)在四川抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过( )
A.66厘米 B.76厘米 C.86厘米 D.96厘米
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com