

17.(2008桂林市)某单位要印刷一批北京奥运会宣传资料,在需要支付制版费600元和每份资料0.3元印刷费的前提下,甲、乙两个印刷厂分别提出了不同的优惠条件,甲印刷厂提出:凡印刷数量超过2000份的,超过部分的印刷费可按9折收费,乙印刷厂提出:凡印刷数量超过3000份的,超过部分印刷费可按8折收费。
(1)如果该单位要印刷2400份,那么甲印刷厂的费用是 ,乙印刷厂费的用是 。
(2)根据印刷数量大小,请讨论该单位到哪家印刷厂印刷资料可获得更大优惠?
解:(1)1308,1320;
(2)设该单位需要印刷资料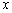 份,
份,
当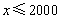 时,甲印刷厂的费用是600+0.3
时,甲印刷厂的费用是600+0.3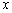 ,乙印刷厂的费用是600+0.3
,乙印刷厂的费用是600+0.3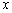 ,两厂的费用相同;
,两厂的费用相同;
当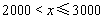 时,甲印刷厂的费用是600+0.3×2000+0.3
时,甲印刷厂的费用是600+0.3×2000+0.3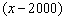 ×90%=0.27
×90%=0.27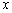 +660,
+660,
乙印刷厂的费用是600+0.3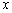 ,甲厂的费用较低;
,甲厂的费用较低;
当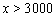 时,甲印刷厂的费用是600+0.3×2000+0.3
时,甲印刷厂的费用是600+0.3×2000+0.3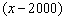 ×90%=0.27
×90%=0.27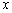 +660,
+660,
乙印刷厂的费用是600+0.3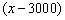 ×80%=0.24
×80%=0.24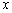 -120,乙厂的费用较低.
-120,乙厂的费用较低.
16.(2008湖北襄樊)“六一”儿童节前夕,某消防队官兵了解到汶川地震灾区一帐篷小学的小朋友喜欢奥运福娃,就特意买了一些,送给这个小学的西欧啊朋友做为节日礼物.如果每班分10套,那么欲5套;如果前面的每个班级分13套,那么最后一个班级虽然分有福娃,但不足4套.问:该小学有多少个班级?奥运福娃共有多少套?
解:设该小学有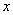 个班,则奥运福娃共有
个班,则奥运福娃共有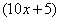 套.
套.
由题意,得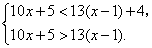 ···················· (3分)
···················· (3分)
解之,得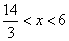 .·························· (5分)
.·························· (5分)
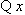 只能取整数,
只能取整数,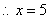 ,此时
,此时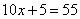 .··············· (6分)
.··············· (6分)
答:该小学有5个班级,共有奥运福娃55套.··············· (7分)
15. (2008永州市)某物流公司,要将300吨物资运往某地,现有A、B两种型号的车可供调用,已知A型车每辆可装20吨,B型车每辆可装15吨,在每辆车不超载的条件下,把300吨物资装运完,问:在已确定调用5辆A型车的前提下至少还需调用B型车多少辆?
解:设还需要B型车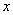 辆,根据题意,得:
辆,根据题意,得:
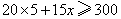 ····························· 3分
····························· 3分
解得: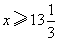 ······························· 5分
······························· 5分
由于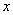 是车的数量,应为整数,所以
是车的数量,应为整数,所以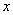 的最小值为14.·············· 7分
的最小值为14.·············· 7分
答:至少需要14台B型车.························· 8分
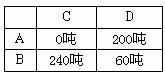
14.(2008湖北咸宁)“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;

设A、B两个蔬菜基地的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少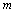 元(
元(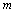 >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.
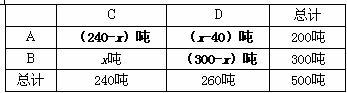 解:(1)填表
解:(1)填表
依题意得: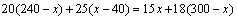 . 解得:
. 解得: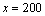 .
.
(2) w与x之间的函数关系为: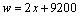 .
.
依题意得: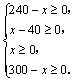 ,∴40≤
,∴40≤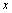 ≤240
≤240
在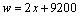 中,∵2>0, ∴
中,∵2>0, ∴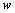 随
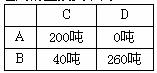
随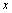 的增大而增大, 表一:
的增大而增大, 表一:
故当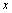 =40时,总运费最小,此时调运方案为如右表一.
=40时,总运费最小,此时调运方案为如右表一.
(3)由题意知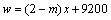
∴0<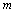 <2时,(2)中调运方案总运费最小;
表二:
<2时,(2)中调运方案总运费最小;
表二:
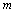 =2时,在40≤
=2时,在40≤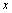 ≤240的前提下调运方案的总运费不变;
≤240的前提下调运方案的总运费不变;
2<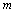 <15时,
<15时,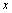 =240总运费最小,其调运方案如右表二 .
=240总运费最小,其调运方案如右表二 .
13.(2008湖北鄂州)为了更好治理洋澜湖水质,保护环境,市治污公司决定购买10台污水处理设备.现有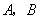 两种型号的设备,其中每台的价格,月处理污水量如下表:
两种型号的设备,其中每台的价格,月处理污水量如下表:
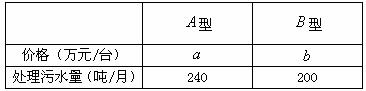
经调查:购买一台 型设备比购买一台
型设备比购买一台 型设备多2万元,购买2台
型设备多2万元,购买2台 型设备比购买3台
型设备比购买3台 型设备少6万元.
型设备少6万元.
(1)求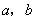 的值.
的值.
(2)经预算:市治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案.
(3)在(2)问的条件下,若每月要求处理洋澜湖的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
解:(1)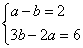 ,
,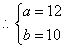 。
。
(2)设购买污水处理设备 型设备
型设备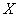 台,
台, 型设备
型设备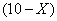 台,则:
台,则: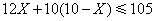
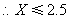 ,
,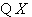 取非负整数,
取非负整数,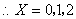 ,
, 有三种购买方案:①
有三种购买方案:① 型设备0台,
型设备0台, 型设备10台;②
型设备10台;② 型设备1台,
型设备1台, 型设备9台;③
型设备9台;③ 型设备2台,
型设备2台, 型设备8台.
型设备8台.
(3)由题意: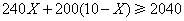 ,
,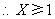 ,又
,又 ,
,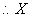 为1,2.
为1,2.
当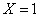 时,购买资金为:
时,购买资金为: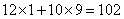 (万元)
(万元)
当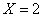 时,购买资金为:
时,购买资金为: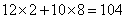 (万元)
(万元)
 为了节约资金,应选购
为了节约资金,应选购 型设备1台,
型设备1台, 型设备9台
型设备9台
12. (2008 湖南 怀化)5.12四川地震后,怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作.拟派30名医护人员,携带20件行李(药品、器械),租用甲、乙两种型号的汽车共8辆,日夜兼程赶赴灾区.经了解,甲种汽车每辆最多能载4人和3件行李,乙种汽车每辆最多能载2人和8件行李.
(1)设租用甲种汽车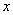 辆,请你设计所有可能的租车方案;
辆,请你设计所有可能的租车方案;
(2)如果甲、乙两种汽车的租车费用每辆分别为8000元、6000元,请你选择最省钱的租车方案.
解: (1)因为租用甲种汽车为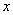 辆,则租用乙种汽车
辆,则租用乙种汽车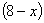 辆.
辆.
由题意,得
解之,得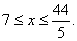
即共有两种租车方案:
第一种是租用甲种汽车7辆,乙种汽车1辆;
第二种是全部租用甲种汽车8辆
(2)第一种租车方案的费用为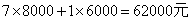
第二种租车方案的费用为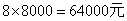
所以第一种租车方案最省钱
11.(2008 河南)某校八年级举行英语演讲比赛,派了两位老师去学校附近的超市购买笔记本作为奖品,经过了解得知,该超市的A,B两种笔记本的价格分别是12元和8元,他们准备购买这两种笔记本共30本。
(1)如果他们计划用300元购买奖品,那么能买这两种笔记本各多少本?
(2)两位老师根据演讲比赛的设奖情况,决定所购买的A种笔记本的数量要少于B种笔记本数量的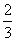 ,但又不少于B种笔记本数量的
,但又不少于B种笔记本数量的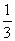 ,如果设他们买A种笔记本n本,买这两种笔记本共花费w元。
,如果设他们买A种笔记本n本,买这两种笔记本共花费w元。
①请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
②请你帮他们计算,购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
解:(1)设能买A种笔记本x本,则能买B种笔记本(30-x)本
依题意得:12x+8(30-x)=300,解得x=15.
因此,能购买A,B两种笔记本各15本 …………………………3分
(2)①依题意得:w=12n+8(30-n),
即w=4n+240,
且n<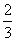 (30-n)和n≥
(30-n)和n≥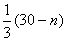
解得 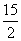 ≤n<12
≤n<12
所以,w(元)关于n(本)的函数关系式为:w=4n+240,
自变量n的取值范围是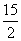 ≤n<12,n为整数。 ………………7分
≤n<12,n为整数。 ………………7分
②对于一次函数w=4n+240,
∵w随n的增大而增大,且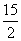 ≤n<12,n为整数,
≤n<12,n为整数,
故当n为8 时,w的值最小
此时,30-n=30-8=22,w=4×8+240=272(元)。
因此,当买A种笔记本8本、B种笔记本22本时,所花费用最少,为272元
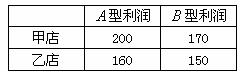
10.(2008湖北黄石)某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
(1)设分配给甲店 型产品
型产品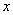 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为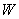 (元),求
(元),求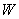 关于
关于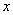 的函数关系式,并求出
的函数关系式,并求出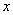 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利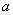 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的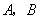 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
解 依题意,甲店 型产品有
型产品有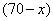 件,乙店
件,乙店 型有
型有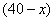 件,
件, 型有
型有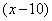 件,则
件,则
(1)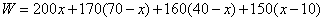
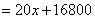 .
.
由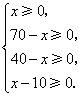 解得
解得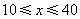 .···················· (2分)
.···················· (2分)
(2)由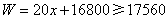 ,
,
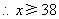 .
.
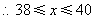 ,
,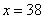 ,39,40.
,39,40.
 有三种不同的分配方案.
有三种不同的分配方案.
①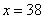 时,甲店
时,甲店 型38件,
型38件, 型32件,乙店
型32件,乙店 型2件,
型2件, 型28件.
型28件.
②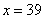 时,甲店
时,甲店 型39件,
型39件, 型31件,乙店
型31件,乙店 型1件,
型1件, 型29件.
型29件.
③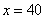 时,甲店
时,甲店 型40件,
型40件, 型30件,乙店
型30件,乙店 型0件,
型0件, 型30件.
型30件.
(3)依题意:
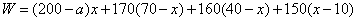
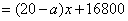 .
.
①当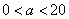 时,
时,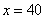 ,即甲店
,即甲店 型40件,
型40件, 型30件,乙店
型30件,乙店 型0件,
型0件, 型30件,能使总利润达到最大.
型30件,能使总利润达到最大.
②当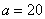 时,
时,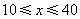 ,符合题意的各种方案,使总利润都一样.
,符合题意的各种方案,使总利润都一样.
③当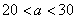 时,
时,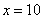 ,即甲店
,即甲店 型10件,
型10件, 型60件,乙店
型60件,乙店 型30件,
型30件, 型0件,能使总利润达到最大. (8分)
型0件,能使总利润达到最大. (8分)
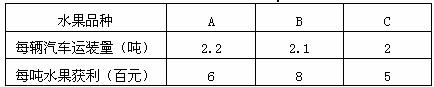
9.(2008年云南省双柏县)我县农业结构调整取得了巨大成功,今年水果又喜获丰收,某乡组织30辆汽车装运A、B、C三种水果共64吨到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆;同时,装运的B种水果的重量不超过装运的A、C两种水果重量之和.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并写出自变量的取值范围.?
(2)设此次外销活动的利润为Q(万元),求Q与x之间的函数关系式,请你提出一个获得最大利润时的车辆分配方案.
解:(1)由题得到:2.2x+2.1y+2(30-x-y)=64 所以 y = -2x+40
又x≥4,y≥4,30-x-y≥4,得到14≤x≤18
(2)Q=6x+8y+5(30-x-y)= -5x+170
Q随着x的减小而增大,又14≤x≤18,所以当x=14时,Q取得最大值,
即Q= -5x+170=100(百元)=1万元。
因此,当x=14时,y = -2x+40=12, 30-x-y=4
所以,应这样安排:A种水果用14辆车,B种水果用12辆车,C种水果用4辆车
8.(2008年山东省青岛市)2008年8月,北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种:A种船票600元/张,B种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A,B两种船票共15张,要求A种船票的数量不少于B种船票数量的一半.若设购买A种船票x张,请你解答下列问题:
(1)共有几种符合题意的购票方案?写出解答过程;
(2)根据计算判断:哪种购票方案更省钱?
解:(1)解:由题意:
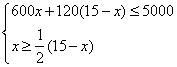 ,………………2分
,………………2分
解得:5≤x≤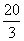 ………………3分
………………3分
∵x为整数,∴x=5,6 ………………4分
∴共两种购票方案:
方案一:A种船票5张,B种船票10张
方案二:A种船票6张,B种船票9张 ………………5分
(2)因为B种船票价格便宜,因此B种船票越多,总购票费用少.
∴第一种方案省钱,为5×600+120×10=4200(元)………………8分
前两年第20题知识点分布:2006年考查内容不等式组设计方案,2007年考查内容不等式组设计方案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com