
3.(2008浙江金华)化简a+b+(a-b)的最后结果是( )
A、2a+2b B、2b C、2a D、0
答案:C
2.(08山东日照)下列计算结果正确的是( )
A. B.
B. =
=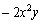
C.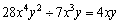 D.
D.
答案:C
1.(2008年四川省宜宾市)下列各式中,计算错误的是( )
A. 2a+3a=5a B. –x2·x= -x3 C. 2x-3x= -1 D.(-x3)2= x6
答案:C
8.(2008年山东省枣庄市)在直角坐标平面中,O为坐标原点,二次函数 的图象与y轴交于点A,与x轴的负半轴交于点B,且
的图象与y轴交于点A,与x轴的负半轴交于点B,且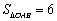 .
.
(1)求点A与点B的坐标;
(2)求此二次函数的解析式;
(3)如果点P在x轴上,且△ABP是等腰三角形,求点P的坐标.
解:(1)由解析式可知,点A的坐标为(0,4). ………………………1分
∵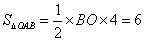 ,∴BO=3.
,∴BO=3.
∴点B的坐标为(-3,0). ………………………………………………………2分
(2)把点B的坐标(-3,0)代入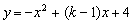 ,得
,得
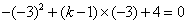 . 解得
. 解得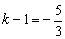 . …………………4分
. …………………4分
∴所求二次函数的解析式为 . …………………………………5分
. …………………………………5分
(3)因为△ABP是等腰三角形,所以
①当AB=AP时,点P的坐标为(3,0). …………………………………………6分
②当AB=BP时,点P的坐标为(2,0)或(-8,0). …………………………8分
③当AP=BP时,设点P的坐标为(x,0).根据题意,得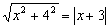 .
.
解得 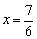 .∴点P的坐标为(
.∴点P的坐标为(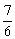 ,0). ……………………………………10分
,0). ……………………………………10分
综上所述,点P的坐标为(3,0)、(2,0)、(-8,0)、(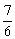 ,0).
,0).
7.(2008年吉林省长春市)已知,如图,直线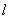 经过
经过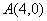 和
和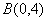 两点,它与抛物线
两点,它与抛物线 在第一象限内相交于点P,又知
在第一象限内相交于点P,又知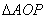 的面积为4,求
的面积为4,求 的值.
的值.

解:由△AOPA的面积可知P是AB的中点,从而可得△OAP是等腰直角三角形,过P作PC⊥OA于C可得P(2,2),所以a=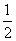
6.(2008年江苏省无锡市)已知抛物线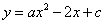 与它的对称轴相交于点
与它的对称轴相交于点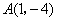 ,与
,与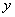 轴交于
轴交于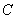 ,与
,与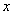 轴正半轴交于
轴正半轴交于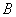 .
.
(1)求这条抛物线的函数关系式;
(2)设直线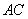 交
交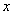 轴于
轴于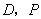 是线段
是线段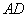 上一动点(
上一动点(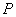 点异于
点异于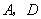 ),过
),过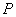 作
作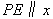 轴交直线
轴交直线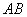 于
于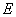 ,过
,过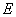 作
作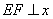 轴于
轴于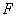 ,求当四边形
,求当四边形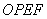 的面积等于
的面积等于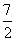 时点
时点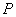 的坐标.
的坐标.
解:(1)由题意,知点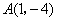 是抛物线的顶点,
是抛物线的顶点,
 ···························· (2分)
···························· (2分)
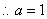 ,
,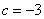 ,
, 抛物线的函数关系式为
抛物线的函数关系式为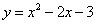 .········ (3分)
.········ (3分)
(2)由(1)知,点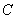 的坐标是
的坐标是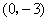 .设直线
.设直线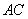 的函数关系式为
的函数关系式为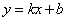 ,
,
则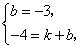
 ,
,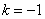 ,
,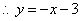
由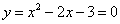 ,得
,得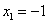 ,
,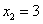 ,
, 点
点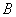 的坐标是
的坐标是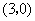 .
.
设直线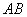 的函数关系式是
的函数关系式是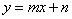 ,
,
则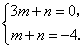 解得
解得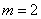 ,
,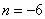 .
.
 直线
直线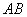 的函数关系式是
的函数关系式是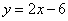 .
.
设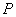 点坐标为
点坐标为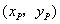 ,则
,则 .
.
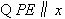 轴,
轴,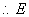 点的纵坐标也是
点的纵坐标也是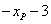 .
.
设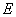 点坐标为
点坐标为 ,
,
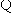 点
点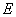 在直线
在直线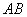 上,
上,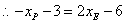 ,
,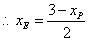 .
.
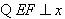 轴,
轴, 点的坐标为
点的坐标为 ,
,
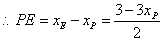 ,
,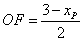 ,
,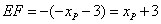 ,
,
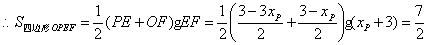 ,
,
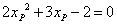 ,
,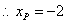 ,
,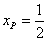 ,当
,当 时,
时,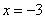 ,
,
而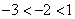 ,
,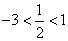 ,
,
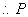 点坐标为
点坐标为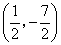 和
和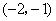 . (9分)
. (9分)
5.(2008年江苏省连云港市)如图,在平面直角坐标系中,点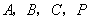 的坐标分别为
的坐标分别为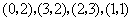 .
.
(1)请在图中画出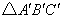 ,使得
,使得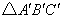 与
与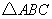 关于点
关于点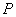 成中心对称;
成中心对称;
(2)若一个二次函数的图象经过(1)中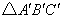 的三个顶点,求此二次函数的关系式.
的三个顶点,求此二次函数的关系式.
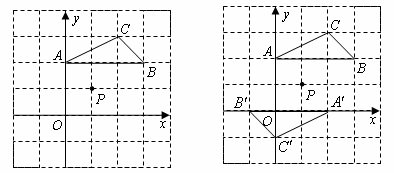
解:(1)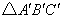 如图所示.
如图所示.
(2)由(1)知,点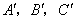 的坐标分别为
的坐标分别为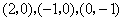 .
.
由二次函数图象与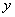 轴的交点
轴的交点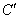 的坐标为
的坐标为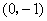 ,
,
故可设所求二次函数关系式为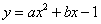 .
.
将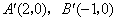 的坐标代入,得
的坐标代入,得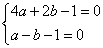 ,解得
,解得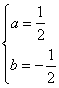 .
.
故所求二次函数关系式为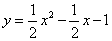 . 8分
. 8分
4.(2008泰州市)已知二次函数y1=ax2+bx+c(a≠0)的图像经过三点(1,0),(-3,0),(0,-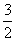 ).
).
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分)
(2)若反比例函数y2=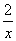 (x>0)的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;(4分)
(x>0)的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;(4分)
(3)若反比例函数y2=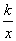 (x>0,k>0)的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.(5分)
(x>0,k>0)的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.(5分)

解:(1)设抛物线解析式为y=a(x-1)(x+3)…………………………1分
(只要设出解析式正确,不管是什么形式给1分)
将(0,-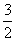 )代入,解得a=
)代入,解得a=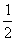 .
.
∴抛物线解析式为y=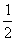 x2+x-
x2+x-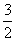 …………………………………3分
…………………………………3分
(无论解析式是什么形式只要正确都得分)
画图(略)。(没有列表不扣分)…………………………………5分
(2)正确的画出反比例函数在第一象限内的图像……………7分
由图像可知,交点的横坐标x0 落在1和2之间,从而得出这两个相邻的正整数为1与2。…………………………………………………9分
(3)由函数图像或函数性质可知:当2<x<3时,
对y1=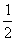 x2+x-
x2+x-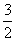 , y1随着x增大而增大,对y2=
, y1随着x增大而增大,对y2=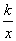 (k>0),
(k>0),
y2随着X的增大而减小。因为A(X0,Y0)为二次函数图像与反比例函数图像的交点,所心当X0=2时,由反比例函数图象在二次函数上方得y2>y1,
即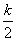 >
>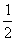 ×22+2-
×22+2-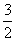 ,解得K>5。…………………………………11分
,解得K>5。…………………………………11分
同理,当X0=3时,由二次函数数图象在反比例上方得y1>y2,
即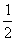 ×32+3-
×32+3-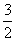 >
>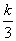 ,解得K<18。…………………………………13
,解得K<18。…………………………………13
所以K的取值范围为5 <K<18………………………………………14分
3.(2008 四川 泸州)如图9, ,
,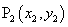 ,……
,……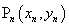 在函数
在函数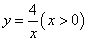 的图像上,
的图像上, ,
,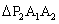 ,
,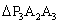 ,……
,……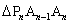 都是等腰直角三角形,斜边
都是等腰直角三角形,斜边 、
、 、
、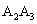 ,……
,……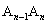 都在
都在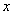 轴上
轴上
⑴求 的坐标
的坐标
⑵求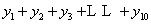 的值
的值
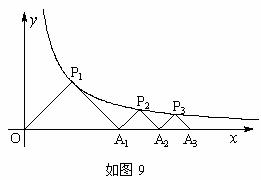
解:(1)由 是等腰直角三角形,得
是等腰直角三角形,得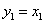 ,则有
,则有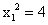 ,故
,故
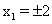 (负舍),点
(负舍),点 (2,2)。
(2,2)。
(2)由题意知
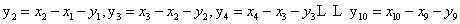
又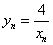 ,则
,则
则 ,故
,故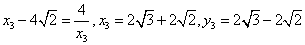 ,同理,依次得
,同理,依次得
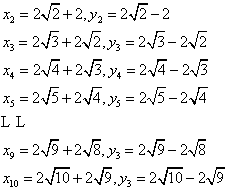
则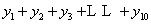
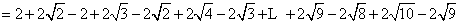
=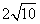 。
。
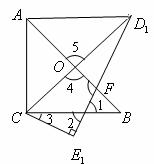
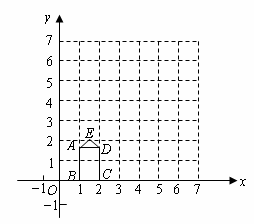
2.(2008年陕西省)如图,矩形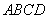 的长、宽分别为
的长、宽分别为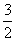 和1,且
和1,且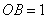 ,点
,点 ,连接
,连接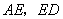 .
.
(1)求经过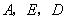 三点的抛物线的表达式;
三点的抛物线的表达式;
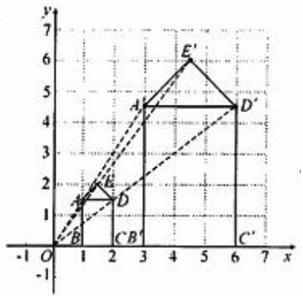
(2)若以原点为位似中心,将五边形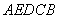 放大,使放大后的五边形的边长是原五边形对应边长的3倍.请在下图网格中画出放大后的五边形
放大,使放大后的五边形的边长是原五边形对应边长的3倍.请在下图网格中画出放大后的五边形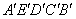 ;
;
(3)经过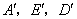 三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.
三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.
解:(1)设经过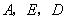 三点的抛物线的表达式为
三点的抛物线的表达式为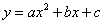 .
.
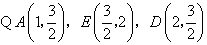 .
.
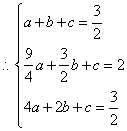 ,
,
解之,得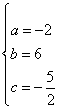 .
.
 过
过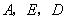 三点的抛物线的表达式为
三点的抛物线的表达式为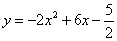 .
.
(3)不能.理由如下:
设经过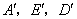 三点的抛物线的表达式为
三点的抛物线的表达式为 .
.
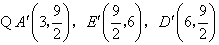 ,
,
 ,解之,得
,解之,得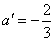 .
.
 ,
,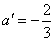 ,
,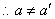 .
.
 经过
经过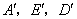 三点的抛物线不能由(1)中抛物线平移得到. (
三点的抛物线不能由(1)中抛物线平移得到. (
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com