
36.(2008湖南益阳市) △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
Ⅰ.证明:△BDG≌△CEF;
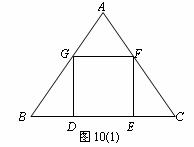
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.
设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
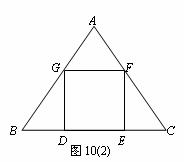
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
Ⅰ.证明:∵DEFG为正方形,
∴GD=FE,∠GDB=∠FEC=90°
∵△ABC是等边三角形,∴∠B=∠C=60°
∴△BDG≌△CEF(AAS)
Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,

求得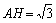
由△AGF∽△ABC得:
解之得: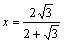 (或
(或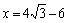 )
)
解法二:设正方形的边长为x,则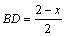
在Rt△BDG中,tan∠B= ,
,
∴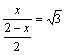
解之得: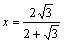 (或
(或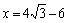 )
)
解法三:设正方形的边长为x,
则
由勾股定理得:
解之得: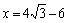
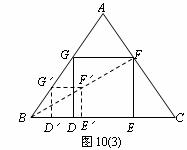
Ⅱb.解: 正确
由已知可知,四边形GDEF为矩形
∵FE∥F’E’ ,
∴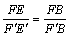 ,
,
同理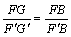 ,
,

∴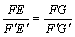
又∵F’E’=F’G’,
∴FE=FG
因此,矩形GDEF为正方形
34.(2008广东肇庆市)如图5,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
cm,求正方形DEFG的边长.

解:(1)∵ 等腰Rt△ABC中,∠ 90°,
90°,
∴ ∠A=∠B
∵ 四边形DEFG是正方形,
∴ DE=GF,∠DEA=∠GFB=90°
∴ △ADE≌△BGF
∴ AE=BF
(2)∵ ∠DEA=90°,∠A=45°
∴ ∠ADE=45°
∴ AE=DE. 同理BF=GF
∴ EF= AB=
AB=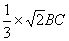 =
=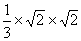 =
= cm
cm
∴
正方形DEFG的边长为
33. (2008黑龙江黑河)已知:正方形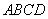 中,
中, ,
, 绕点
绕点 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交 (或它们的延长线)于点
(或它们的延长线)于点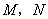 .
.
当 绕点
绕点 旋转到
旋转到 时(如图1),易证
时(如图1),易证 .
.
(1)当 绕点
绕点 旋转到
旋转到 时(如图2),线段
时(如图2),线段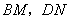 和
和 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当 绕点
绕点 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段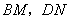 和
和 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.

.
解:(1) 成立.
成立.
如图,把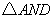 绕点
绕点 顺时针
顺时针 ,得到
,得到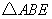 ,
,
则可证得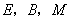 三点共线(图形画正确)
三点共线(图形画正确)
证明过程中,
证得: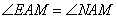
证得:



(2)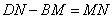
28.(2008湖北黄冈)已知:如图,点 是正方形
是正方形 的边
的边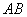 上任意一点,过点
上任意一点,过点 作
作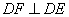 交
交 的延长线于点
的延长线于点 .求证:
.求证: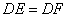 .
.

解:∵ 四边形ABCD是正方形,
∴ AD=CD ,∠A=∠DCF=900
又∵ DF⊥DE,
∴ ∠1+∠3=∠2+∠3
∴ ∠1=∠2
在Rt△DAE和Rt△DCE中,
∠1=∠2
AD=CD
∠A=∠DCF
∴ Rt△DAE Rt△DCE
Rt△DCE
∴ DE=DF.
23.(2008泰州市)在矩形ABCD中,AB=2,AD= .
.
(1)在边CD上找一点E,使EB平分∠AEC,并加以说明;(3分)
(2)若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.
①求证:点B平分线段AF;(3分)
②△PAE能否由△PFB绕P点按顺时针方向旋转而得到,若能,加以证明,并求出旋转度数;若不能,请说明理由.(4分)

解:(1)当E为CD中点时,EB平分∠AEC
由∠D=900 ,DE=1,AD= ,推得DEA=600,
,推得DEA=600,
同理,∠CEB=600 ,从而∠AEB=∠CEB=600 ,即EB平分∠AEC
(2)① ∵CE∥BF
∴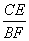 =
= =
=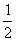 ∴BF=2CE
∴BF=2CE
∵AB=2CE,
∴点B平分线段AF
②能。
证明:∵CP=
 ,CE=1,∠C=900
,CE=1,∠C=900
∴EP=
 。
。
在Rt △ADE中,AE= 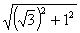 =2
=2
∴AE=BF,
又∵PB= ,
,
∴PB=PE
∵∠AEP=∠BP=900 ,
∴△PAS≌△PFB。
∴△PAE可以△PFB按照顺时针方向绕P点旋转而得到。
旋转度数为1200
20.(2008湖北襄樊)如图12,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG、DE.
(1)观察猜想BG与DE之间的大小关系,并证明你的结论.
(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
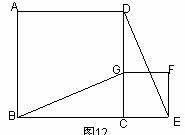
解:(1)BG=DE
∵四边形ABCD和四边形CEFG都是正方形,
∴GC=CE,BC=CD,∠BCG=∠DCE=90°)
∴△BCG≌△DCE
∴BG=DE
(2)存在. △BCG和△DCE
△BCG绕点C顺时针方向旋转90°与△DCE重合
12.(2008年江苏省无锡市)如图,已知 是矩形
是矩形 的边
的边 上一点,
上一点, 于
于 ,试说明:
,试说明: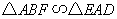 .
.
解法一: 矩形
矩形 中,
中, ,
,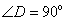
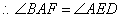
 ,
,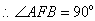 ,
,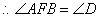

解法二: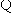 矩形
矩形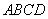 中,
中,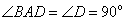
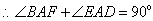 ,
, ,
,
 .
.
11.(2008年山东省青岛市)已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形?并说明理由
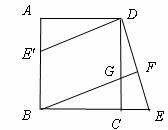
解:(1)证明:∵四边形为正方形
∴BC=CD,∠BCG=∠DCE=90°
∵CG=CE,
∴△BCG≌△DCE
(2)答:四边形E′BGD是平行四边形
理由:
∵△DCE绕点D顺时针旋转90°得到△DAE′
∴CE=AE′
∵CG=CE
∴CG=AE′
∵AB=CD,AB∥CD,
∴BE′=DG,BE′∥DG,
∴四边形E′BGD是平行四边形
15.
(2008遵义)现有三个多项式: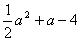 ,
,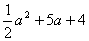 ,
, ,请你选择其中两个进行加法运算,并把结果因式分解。
,请你选择其中两个进行加法运算,并把结果因式分解。
解:(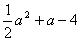 )+(
)+( )=
)=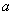 2-4=(
2-4=(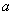 +2)(
+2)(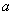 -2)
-2)
14.(2008徐州)已知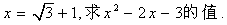
解: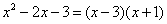 ,将
,将 代入到上式,则可得
代入到上式,则可得

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com