
4. (2008年四川省宜宾市)若方程组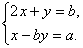 的解是
的解是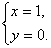 ,那么
,那么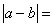
答案:1
3. (2008 重庆)方程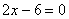 的解为
.
的解为
.
答案: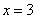
2. (2008 湖南 怀化)方程组 的解是
___.
的解是
___.
答案: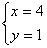
1. (2008 山东 临沂)已知x、y满足方程组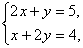 则x-y的值为________.
则x-y的值为________.
答案:1
5. (2008 湖北 荆门)用四个全等的矩形和一个小正方形拼成如图所示的大正
方形,已知大正方形的面积是144,小正方形的面积是4,
若用x,y表示矩形的长和宽(x>y),则下列关系式中不正
确的是( ) D
(A) x+y=12 . (B) x-y=2.
(C) xy=35. (D) x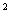 +y
+y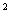 =144.
=144.

答案:D
4. (2008义乌)已知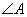 、
、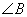 互余,
互余,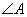 比
比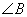 大
大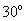 .设
.设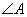 、
、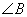 的度数分别为
的度数分别为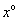 、
、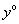 ,下列方程组中符合题意的是( )
,下列方程组中符合题意的是( )
A.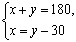 B.
B. 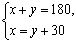 C.
C.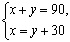 D.
D.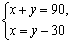
答案:C
3. (2008山东济南).如果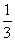 xa+2y3与-3x3y2b-1是同类项,那么a、b的值分别是( )
xa+2y3与-3x3y2b-1是同类项,那么a、b的值分别是( )
A.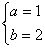 B.
B.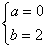 C.
C.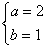 D.
D.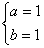
答案:A
2. (2008 湖北 十堰)把方程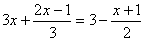 去分母正确的是( )
去分母正确的是( )
A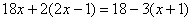 B
B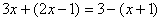 C.
C.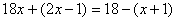 D.
D.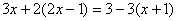
答案:A
1. (2008 台湾)若二元一次联立方程式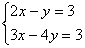 的解为x=a,y=b,则a+b=?( )
(A)
1 (B) 6 (C)
的解为x=a,y=b,则a+b=?( )
(A)
1 (B) 6 (C) 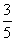 ((D)
((D) 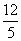 。
。
答案:D
5、解:(1)∵DE∥BC,
∴∠EDB=∠DBC=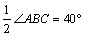
(2) ∵AB=BC, BD是∠ABC的平分线,
∴D为AC的中点
∵DE∥BC,∴E为AB的中点,
∴DE=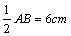
(28) (2008 福建 龙岩)如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并给予证明.
我找的等腰三角形是: .
证明:
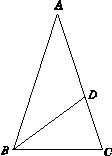
所找的等腰三角形是:△ABC(或△BDC或△DAB)
证明:在△ABC中,
∵∠A=36°,∠C=72°,
∴∠ABC=180°-(72°+36°)=72°.
∵∠C=∠ABC,
∴AB=AC,
∴△ABC是等腰三角形.
[注]若找△BDC或△DAB参照给分.
(29)(2008 四川 内江)如图,在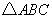 中,点
中,点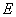 在
在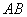 上,点
上,点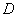 在
在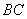 上,
上,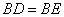 ,
,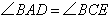 ,
, 与
与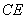 相交于点
相交于点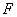 ,试判断
,试判断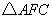 的形状,并说明理由.
的形状,并说明理由.
简证:由条件可证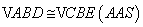
故可证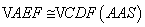 ,
,
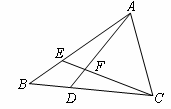
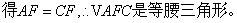
(30)(2008年湖北省咸宁市)如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.
(1) 试探究A E与⊙O的位置关系,并说明理由;
(2) 已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,设计出计算⊙O的半径r的一种方案:
①你选用的已知数是 ;
②写出求解过程(结果用字母表示).
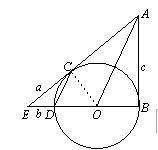
解:(1)A E与⊙O相切
理由:连接OC .
∵CD∥OA
∴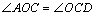 ,
,
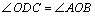
又∵OD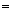 OC,
OC,
∴
∴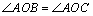
在△AOC和△AOB中
OA=OA,
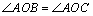 ,OB=OC
,OB=OC
∴△AOC≌△AOB, ∴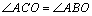
∵AB与⊙O相切, ∴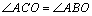 =90°
=90°
∴A E与⊙O相切
(2) ①选择a、b、c,或其中2个
② 解答举例:
若选择a、b、c,
方法一:由CD∥OA, 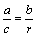 ,得
,得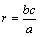 .
.
方法二:在Rt△ABE中 ,由勾股定理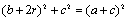 ,
,
得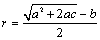 .
.
方法三:由Rt△OCE∽Rt△ABE,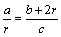 ,得
,得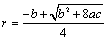 .
.
若选择a、b
方法一:在Rt△OCE中 ,由勾股定理: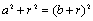 ,得
,得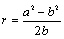 ;
;
方法二:连接BC,由△DCE∽△CBE,得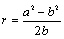 .
.
若选择a、c;需综合运用以上多种方法,得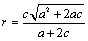 .
.
(31) (2008年宁波市)如图,点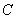 是半圆
是半圆 的半径
的半径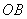 上的动点,作
上的动点,作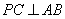 于
于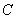 .点
.点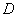 是半圆上位于
是半圆上位于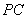 左侧的点,连结
左侧的点,连结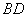 交线段
交线段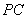 于
于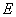 ,且
,且 .
.
(1)求证: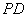 是
是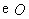 的切线.
的切线.
(2)若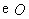 的半径为
的半径为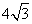 ,
,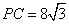 ,设
,设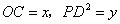 .
.
①求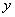 关于
关于 的函数关系式.
的函数关系式.
②当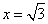 时,求
时,求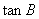 的值.
的值.
解:(1)连结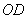 ,
,
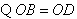 ,
,
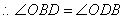
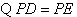 ,
,
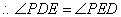
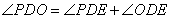
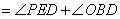
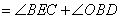
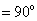
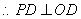
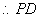 是圆
是圆 的切线
的切线
(2)①连结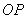 ,
,
在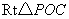 中,
中,
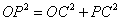
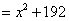
在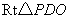 中
中
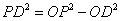
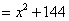 .
.
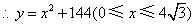
②当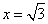 时,
时,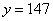 ,
,
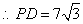
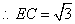
而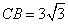
在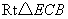 中
中
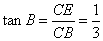
(32)(2008年义乌市)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度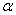 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
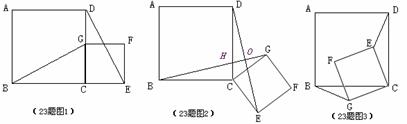
(2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a b,k
b,k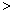 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
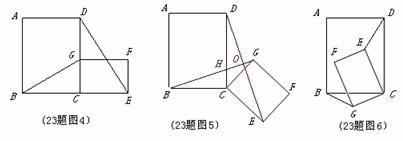
(3)在第(2)题图5中,连结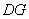 、
、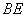 ,且a=3,b=2,k=
,且a=3,b=2,k=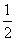 ,求
,求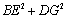 的值.
的值.
解:(1)
①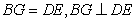
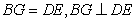 仍然成立
仍然成立
在图(2)中证明如下
∵四边形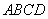 、四边形
、四边形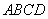 都是正方形
都是正方形
∴ 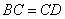 ,
,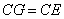 ,
,
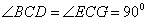
∴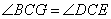
∴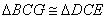 (SAS)
(SAS)
∴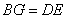
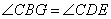
又∵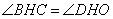
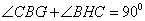
∴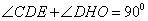 ∴
∴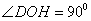
∴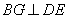
(2)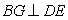 成立,
成立,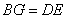 不成立
不成立
简要说明如下
∵四边形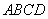 、四边形
、四边形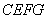 都是矩形,
都是矩形,
且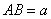 ,
,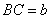 ,
, ,
,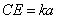 (
(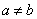 ,
,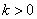 )
)
∴ 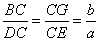 ,
,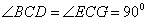
∴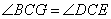
∴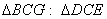
∴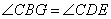
又∵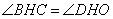
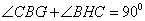
∴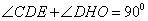 ∴
∴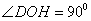
∴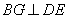
(3)∵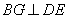
∴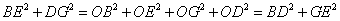
又∵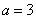 ,
,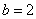 ,
,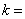
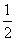
∴
∴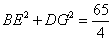
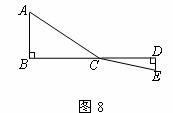
(33)(2008恩施自治州)如图8,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式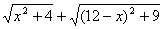 的最小值.
的最小值.
解: (1)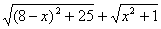
(2)当A、C、E三点共线时,AC+CE的值最小
(3)如下图所示,作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连结交BD于点C.AE的长即为代数式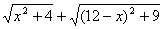 的最小值.
的最小值.
过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,
则AB=DF=2,AF=BD=8.
所以AE=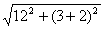 =13
=13
即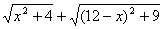 的最小值为13.
的最小值为13.
(34)(2008年广东湛江市)25. 如图9所示,已知AB为⊙O的直径,CD是弦,且AB CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.
(1)求证: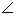 ACO=
ACO=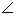 BCD.
BCD.
(2)若EB=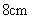 ,CD=
,CD=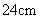 ,求⊙O的直径.
,求⊙O的直径.
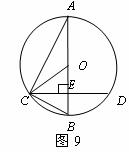

证明:(1)∵AB为⊙O的直径,CD是弦,且AB CD于E,
CD于E,
∴CE=ED, 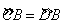
∴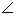 BCD=
BCD=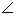 BAC
BAC
∵OA=OC
∴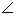 OAC=
OAC=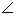 OCA
OCA
∴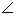 ACO=
ACO=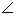 BCD
BCD
(2)设⊙O的半径为Rcm,则OE=OB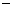 EB=R
EB=R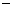 8
8
CE=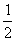 CD=
CD=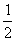
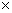 24=12
24=12
在Rt CEO中,由勾股定理可得
CEO中,由勾股定理可得
OC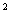 =OE
=OE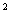 +CE
+CE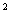 即R
即R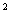 = (R
= (R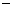 8)
8)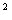 +12
+12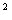
解得 R=13 ∴2R=2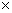 13=26
13=26
答:⊙O的直径为26cm.
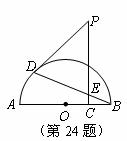
(35)(2008年上海市) “创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆 的半径
的半径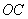 所在的直线为对称轴的轴对称图形,
所在的直线为对称轴的轴对称图形,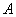 是
是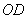 与圆
与圆 的交点.
的交点.
(1)请你帮助小王在下图中把图形补画完整;
(2)由于图纸中圆 的半径
的半径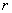 的值已看不清楚,根据上述信息(图纸中
的值已看不清楚,根据上述信息(图纸中 是坡面
是坡面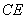 的坡度),求
的坡度),求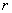 的值.
的值.
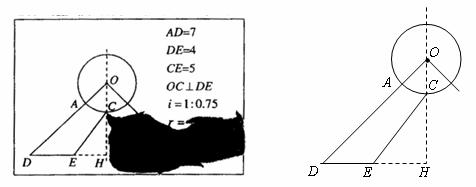
(1)(图形正确)
(2)解:由已知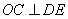 ,垂足为点
,垂足为点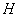 ,则
,则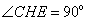
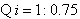 ,
,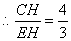
在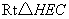 中,
中,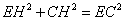 .设
.设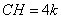 ,
,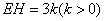 ,又
,又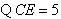
得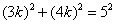 ,解得
,解得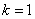 .
.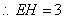 ,
,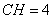
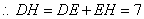 ,
,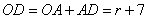 ,
,
在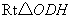 中,
中,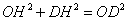 ,
,
解得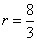
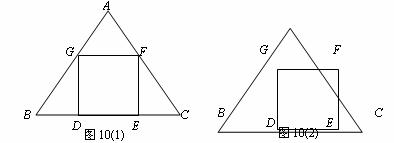
(36)(2008年益阳) △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出
正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了. 设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,
GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
Ⅰ.证明:∵DEFG为正方形,
∴GD=FE,∠GDB=∠FEC=90°
∵△ABC是等边三角形,
∴∠B=∠C=60°
∴△BDG≌△CEF(AAS)
Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,
求得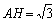
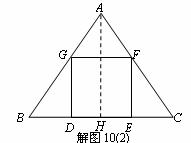
由△AGF∽△ABC得: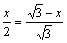
解之得: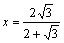 (或
(或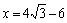 )
)
解法二:设正方形的边长为x,则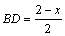
在Rt△BDG中,tan∠B=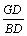 ,
,
∴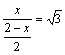
解之得: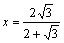 (或
(或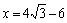 )
)
解法三:设正方形的边长为x,
则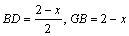
由勾股定理得: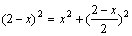
解之得: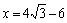
Ⅱb.解: 正确
由已知可知,四边形GDEF为矩形
∵FE∥F’E’ ,
∴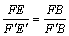 ,
,
同理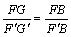 ,
,
∴
又∵F’E’=F’G’,
∴FE=FG
因此,矩形GDEF为正方形

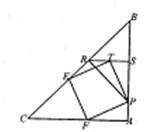
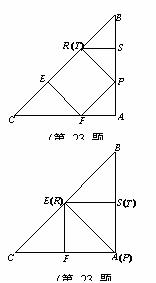
(37)(2008年湖北省宜昌市)如图,在Rt△ABC中,AB=AC,P是边AB(含端点)上的动点,过P作BC的垂线PR,R为垂足,∠PRB的平分线与AB相交于点S,在线段RS上存在一点T,若以线段PT为一边作正方形PTEF,其顶点E、F恰好分别在边BC、AC上.
(1)△ABC与△SBR是否相似?说明理由;
(2)请你探索线段TS与PA的长度之间的关系;
(3)设边AB=1,当P在边AB(含端点)上运动时,请你探索正方形PTEF的面积y的最小值和最大值.
解:(1)∵RS是直角∠PRB的平分线,
∴∠PRS=∠BRS=45°.
在△ABC与△SBR中,∠C=∠BRS=45°,∠B是 公共角,
∴△ABC∽△SBR..
(2)线段TS的长度与PA相等.
∵四边形PTEF是正方形,
∴PF=PT,∠SPT+∠FPA=180°-∠TPF=90°,
在Rt△PFA中,∠PFA +∠FPA=90°,
∴∠PFA=∠TPS,
∴Rt△PAF≌Rt△TSP,
∴PA=TS.
当点P运动到使得T与R重合时,
这时△PFA与△TSP都是等腰直角三角形且底边相等,即有PA=TS.
(若下面解题中没有求出x的取值范围是0≤x≤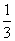 ,以上的讨论可评1分)
,以上的讨论可评1分)
由以上可知,线段ST的长度与PA相等.
(3)由题意,RS是等腰Rt△PRB的底边PB上的高,
∴PS=BS, ∴BS+PS+PA=1, ∴PS=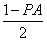 .
.
设PA的长为x,易知AF=PS,
则y=PF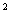 =PA
=PA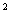 +PS
+PS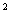 ,得y=x
,得y=x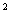 +(
+(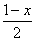 )
)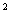 ,
,
即y=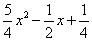
根据二次函数的性质,当x=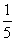 时,y有最小值为
时,y有最小值为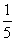 .
.
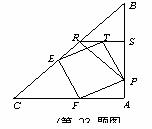
如图2,当点P运动使得T与R重合时,PA=TS为最大.
易证等腰Rt△PAF≌等腰Rt△PSR≌等腰Rt△BSR,
∴PA=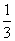 .
.
如图3,当P与A重合时,得x=0.
∴x的取值范围是0≤x≤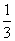 . (此处为独立得分点,只要求出x≤
. (此处为独立得分点,只要求出x≤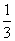 即可得1分)
即可得1分)
∴①当x的值由0增大到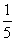 时,y的值由
时,y的值由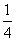 减小到
减小到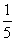
∴②当x的值由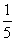 增大到
增大到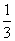 时,y的值由
时,y的值由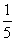 增大到
增大到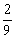 .
.
(说明:①②任做对一处评1分,两处全对也只评一分)
∵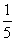 ≤
≤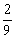 ≤
≤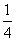 ,∴在点P的运动过程中,
,∴在点P的运动过程中,
正方形PTEF面积y的最小值是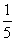 ,y的最大值是
,y的最大值是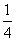 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com