13，已知分式­­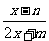,­当x＝3时，­值为0；当x＝－5时,­没有意义.­则­n＝＿＿＿，m＝＿＿＿.

14，如图6有两棵树,一棵高8m,另一棵高2m,两树相距8m, 一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了＿＿＿m.

15，两位同学在描述同一反比例函数的图象时，甲同学说：这个反比例函数图象上任意一点到两坐标轴的距离的积都是3；乙同学说：这个反比例函数的图象与直线y＝x有两个交点，你认为这两位同学所描述的反比例函数的解析式是＿＿＿.

16，华山鞋厂为了了解初中学生穿鞋的鞋号情况,对永红中学八年级(1)班的20名男生所穿鞋号统计如下表:

那么这20名男生鞋号数据的平均数是＿＿＿，中位数是＿＿＿；在平均数、中位数和众数中,鞋厂最感兴趣的是＿＿＿.　

17，为了缓解旱情,我市发射增雨火箭,实施增雨作业,在一场降雨中,某县测得10个面积相等区域的降雨量如下表:

则该县这10个区域降雨量的众数为＿＿＿ (mm)，平均降雨量为＿＿＿ (mm).　

18，一个射箭运动员连续射靶5次,所得环数分别是8,6,10,7,9,则这个运动员所得环数的标准差为＿＿＿.　

19，已知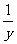－＝4­，则­­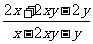的值­为＿＿＿.

20，化简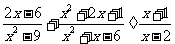：得＿＿＿.　

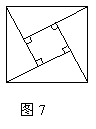
21，2002年8月,在北京召开国际数学大会,大会会标是由4 个相同的直角三角形和1个小正方形拼成的大正方形(如图7),若大正方形的面积是34,小正方形的面积是4,则每个直角三角形的周长是＿＿＿.　

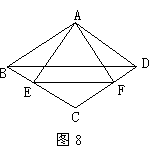
22，如图8,在菱形ABCD中,∠B＝∠EAF＝60°,∠BAE＝20°，则∠CEF的大小为＿＿＿.　

23，我们学习过反比例函数.例如,当矩形面积s一定时,长a是宽b 的反比例函数,其函数关系式可以写为a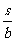＝ (s为常数,s≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:＿＿＿，函数关系式:＿＿＿.

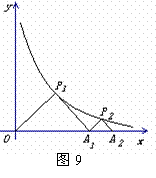
24，如图9，△P₁OA₁、△PA₁A₂是等腰直角三角形,点P₁、P₂在函数y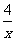＝(x＞0)的图象上，斜边OA₁、A₁A₂都在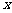轴上，则点A₂的坐标是＿＿＿.

29. 某新建商场设有百货部、服装部和家电部三个经营部，共有190名售货员，计划全商场日营业额(指每日卖出商品所收到的总金额)为60万元，由于营业性质不同，分配到三个部的售货员的人数也就不等。根据经验，各部门每1万元营业额所需售货员人数和每1万元营业额所得利润情况如下表。

商场将计划日营业额分配给三个营业部，设分配给百货部、服装部和家电部的营业额分别为x(万元)，y(万元)和z(万元)(x、y、z都是整数)

(1)请用含x的代数式分别表示y和z；

(2)若商场预计每日的利润为C(万元)，且C满足19≤C≤19.7，问这个商场应怎样分配日营业额给三个营业部？各部应分别安排多少名售货员？

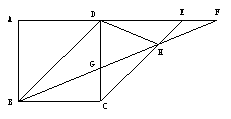
28. 已知：如图，四边形ABCD是正方形，E、F是AD延长线上的点，且DE=DC，DF=BD，求证：DH=GH

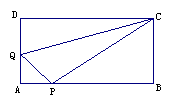
27. 在矩形ABCD中，AB=12cm，BC=6cm。点P沿AB边从点A开始向B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动，如果P、Q同时出发，用t表示时间(0≤t≤6)，那么(1)当t为何值时△QAP为等腰三角形。(2)求四边形QAPC的面积？并提出一个与计算结果有关的结论。(5分)

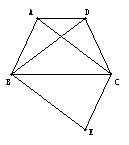
26. 已知：如图，梯形ABCD中，AD∥BC，AB=CD，点D与点E关于BC对称。

(1)四边形ABEC是平行四边形吗？为什么？

(2)若AB=AD=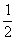BC，说明四边形ABEC为矩形。(6分)

25. 关于x、y的方程组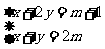的解满足x、y均小于2，求m的取值范围。(6分)

1. 　　　　　　　2. 　　　　　　3. 　　　　　　4. 　　　　　

乙组：

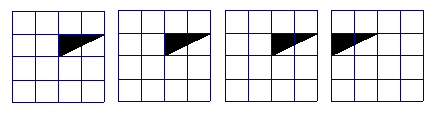
1　　　　　　　 2　　　　　　　 3　　　　　　　 4　　　　

24. (1)分别观察甲组4个小题中的图形，看看每小题中的深色三角形是经过怎样的变换，变成浅色三角形的，并将各小题图形变换的规律填在横线上。(如，平移变换，旋转变换，中心对称，轴对称或几种变换的组合)

　 (2)按照你找出的甲组中各小题图形变换规律，将乙组对应小题中的图形进行相应的变换，并用阴影表示出变换后的图形。(即用甲组第1小题的图形变换规律，将乙组第1小题的图形变换，并画出图形，依次类推)

(每空1分，共8分)

甲组：

1　　　　　　　 2　　　　　　　 3　　　　　　　 4

变换规律：