
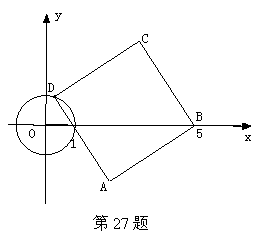
59.(08浙江宿迁)27.(本题满分12分)
如图,⊙ 的半径为
的半径为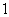 ,正方形
,正方形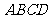 顶点
顶点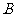 坐标为
坐标为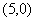 ,顶点
,顶点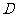 在⊙
在⊙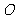 上运动.
上运动.
(1)当点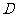 运动到与点
运动到与点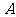 、
、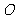 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线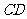 与⊙
与⊙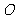 相切;
相切;
(2)当直线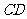 与⊙
与⊙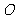 相切时,求
相切时,求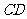 所在直线对应的函数关系式;
所在直线对应的函数关系式;
 (3)设点
(3)设点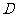 的横坐标为
的横坐标为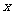 ,正方形
,正方形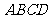 的面积为
的面积为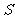 ,求
,求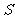 与
与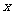 之间的函数关系式,并求出
之间的函数关系式,并求出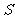 的最大值与最小值.
的最大值与最小值.
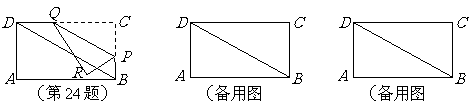
(08浙江宿迁24题解析)24.如图,在矩形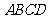 中,
中,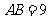 ,
,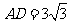 ,点
,点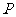 是边
是边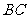 上的动点(点
上的动点(点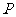 不与点
不与点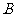 ,点
,点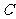 重合),过点
重合),过点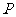 作直线
作直线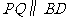 ,交
,交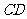 边于
边于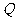 点,再把
点,再把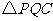 沿着动直线
沿着动直线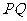 对折,点
对折,点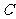 的对应点是
的对应点是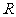 点,设
点,设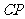 的长度为
的长度为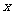 ,
,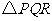 与矩形
与矩形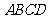 重叠部分的面积为
重叠部分的面积为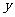 .
.
(1)求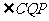 的度数;
的度数;
(2)当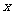 取何值时,点
取何值时,点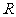 落在矩形
落在矩形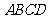 的
的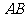 边上?
边上?
(3)①求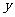 与
与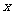 之间的函数关系式;
之间的函数关系式;
②当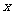 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的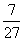 ?
?
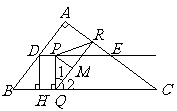
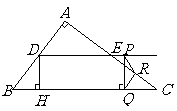
60(08浙江温州)24.(本题14分)
如图,在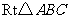 中,
中,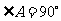 ,
,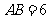 ,
,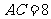 ,
,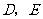 分别是边
分别是边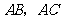 的中点,点
的中点,点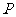 从点
从点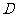 出发沿
出发沿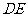 方向运动,过点
方向运动,过点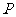 作
作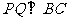 于
于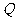 ,过点
,过点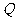 作
作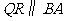 交
交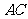 于
于
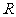 ,当点
,当点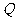 与点
与点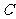 重合时,点
重合时,点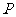 停止运动.设
停止运动.设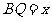 ,
,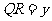 .
.
(1)求点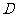 到
到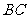 的距离
的距离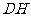 的长;
的长;
(2)求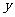 关于
关于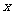 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
 (3)是否存在点
(3)是否存在点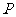 ,使
,使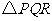 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的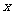 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(08浙江温州24题解析)24. (本题14分)
解:(1)
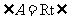 ,
,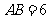 ,
,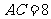 ,
,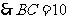 .
.
 点
点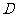 为
为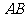 中点,
中点,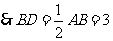 .
.
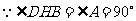 ,
,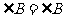 .
.
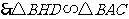 ,
,
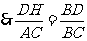 ,
,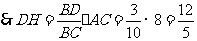 .
.
(2)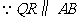 ,
,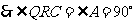 .
.
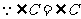 ,
,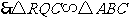 ,
,
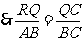 ,
,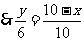 ,
,
即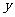 关于
关于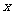 的函数关系式为:
的函数关系式为: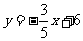 .
.
(3)存在,分三种情况:
 ①当
①当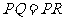 时,过点
时,过点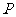 作
作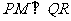 于
于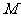 ,则
,则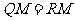 .
.
 ,
,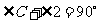 ,
,
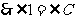 .
.
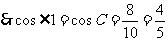 ,
,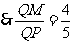 ,
,
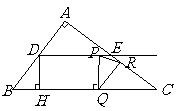
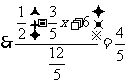 ,
,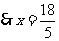 .
.
 ②当
②当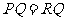 时,
时,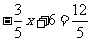 ,
,
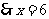 .
.
③当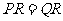 时,则
时,则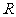 为
为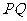 中垂线上的点,
中垂线上的点,
于是点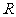 为
为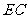 的中点,
的中点,
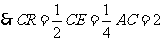 .
.
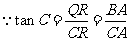 ,
,
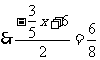 ,
,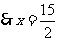 .
.
综上所述,当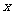 为
为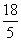 或6或
或6或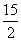 时,
时,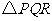 为等腰三角形.
为等腰三角形.
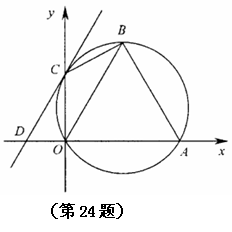
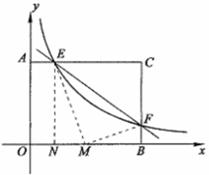
54.(08浙江嘉兴)24.如图,直角坐标系中,已知两点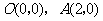 ,点
,点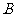 在第一象限且
在第一象限且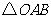 为正三角形,
为正三角形,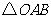 的外接圆交
的外接圆交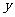 轴的正半轴于点
轴的正半轴于点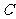 ,过点
,过点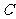 的圆的切线交
的圆的切线交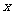 轴于点
轴于点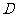 .
.
(1)求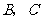 两点的坐标;
两点的坐标;
(2)求直线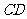 的函数解析式;
的函数解析式;
(3)设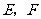 分别是线段
分别是线段 上的两个动点,且
上的两个动点,且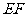 平分四边形
平分四边形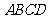 的周长.
的周长.
试探究: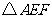 的最大面积?
的最大面积?
(08浙江嘉兴24题解析)24.(1)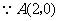 ,
,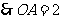 .
.
作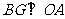 于
于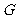 ,
,
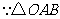 为正三角形,
为正三角形,
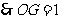 ,
, .
.
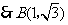 .
.
连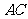 ,
,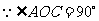 ,
, ,
,
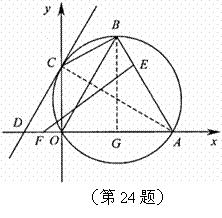
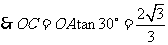 .
.
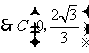 .
.
(2)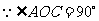 ,
,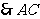 是圆的直径,
是圆的直径,
又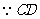 是圆的切线,
是圆的切线,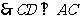 .
.
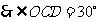 ,
,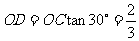 .
.
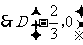 .
.
设直线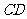 的函数解析式为
的函数解析式为 ,
,
则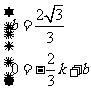 ,解得
,解得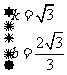 .
.
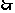 直线
直线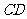 的函数解析式为
的函数解析式为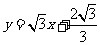 .
.
(3)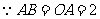 ,
,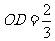 ,
,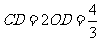 ,
,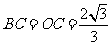 ,
,
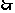 四边形
四边形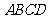 的周长
的周长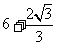 .
.
设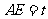 ,
,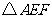 的面积为
的面积为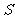 ,
,
则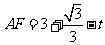 ,
,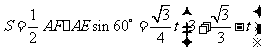 .
.
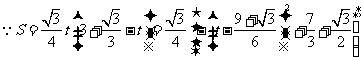 .
.
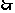 当
当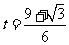 时,
时,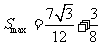 .
.
 点
点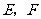 分别在线段
分别在线段 上,
上,
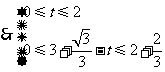 ,解得
,解得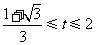 .
.
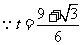 满足
满足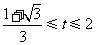 ,
,
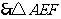 的最大面积为
的最大面积为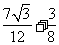 .
.
55(08浙江金华)(本题答案暂缺)24.
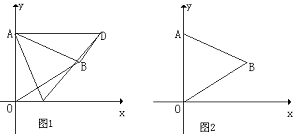
(本题12分) 如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD。(1)求直线AB的解析式;(2)当点P运动到点(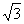 ,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于
,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于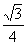 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
56(08浙江丽水)24.如图,在平面直角坐标系中,已知点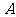 坐标为(2,4),直线
坐标为(2,4),直线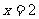 与
与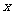 轴相交于点
轴相交于点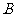 ,连结
,连结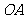 ,抛物线
,抛物线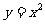 从点
从点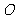 沿
沿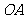 方向平移,与直线
方向平移,与直线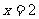 交于点
交于点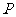 ,顶点
,顶点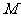 到
到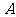 点时停止移动.
点时停止移动.
 (1)求线段
(1)求线段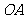 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点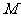 的横坐标为
的横坐标为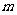 ,
,
①用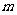 的代数式表示点
的代数式表示点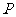 的坐标;
的坐标;
②当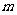 为何值时,线段
为何值时,线段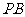 最短;
最短;
(3)当线段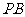 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点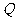 ,使△
,使△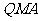
的面积与△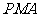 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点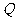 的坐标;若
的坐标;若
不存在,请说明理由.
(08浙江丽水24题解析)24.(本题14分)
解:(1)设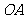 所在直线的函数解析式为
所在直线的函数解析式为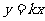 ,
,
∵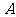 (2,4),
(2,4),
∴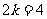 ,
, 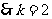 ,
,
∴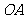 所在直线的函数解析式为
所在直线的函数解析式为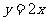 .…………………………………(3分)
.…………………………………(3分)
(2)①∵顶点M的横坐标为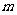 ,且在线段
,且在线段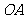 上移动,
上移动,
∴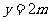 (0≤
(0≤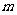 ≤2).
≤2).
∴顶点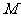 的坐标为(
的坐标为(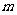 ,
,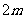 ).
).
∴抛物线函数解析式为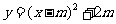 .
.
∴当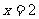 时,
时,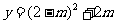
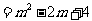 (0≤
(0≤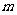 ≤2).
≤2).
∴点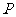 的坐标是(2,
的坐标是(2,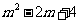 ).…………………………………(3分)
).…………………………………(3分)
② ∵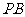 =
=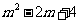 =
=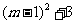 , 又∵0≤
, 又∵0≤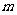 ≤2,
≤2,
∴当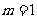 时,PB最短.
……………………………………………(3分)
时,PB最短.
……………………………………………(3分)
(3)当线段 最短时,此时抛物线的解析式为
最短时,此时抛物线的解析式为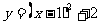 .……………(1分)
.……………(1分)
假设在抛物线上存在点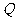 ,使
,使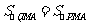 .
.
设点 的坐标为(
的坐标为(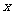 ,
,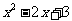 ).
).
①当点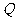 落在直线
落在直线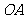 的下方时,过
的下方时,过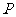 作直线
作直线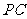 //
//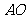 ,交
,交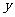 轴于点
轴于点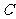 ,
,
∵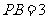 ,
,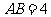 ,
,
∴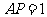 ,∴
,∴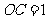 ,∴
,∴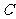 点的坐标是(0,
点的坐标是(0,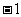 ).
).
 ∵点
∵点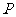 的坐标是(2,3),∴直线
的坐标是(2,3),∴直线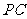 的函数解析式为
的函数解析式为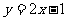 .
.
∵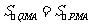 ,∴点
,∴点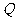 落在直线
落在直线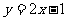 上.
上.
∴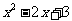 =
=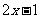 .
.
解得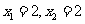 ,即点
,即点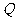 (2,3).
(2,3).
∴点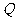 与点
与点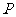 重合.
重合.
∴此时抛物线上不存在点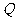 ,使△
,使△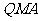 与
与
△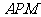 的面积相等.………………………(2分)
的面积相等.………………………(2分)
②当点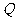 落在直线
落在直线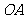 的上方时,
的上方时,
作点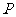 关于点
关于点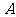 的对称称点
的对称称点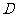 ,过
,过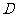 作直线
作直线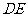 //
//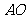 ,交
,交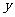 轴于点
轴于点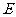 ,
,
∵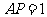 ,∴
,∴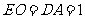 ,∴
,∴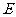 、
、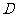 的坐标分别是(0,1),(2,5),
的坐标分别是(0,1),(2,5),
∴直线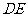 函数解析式为
函数解析式为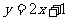 .
.
∵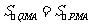 ,∴点
,∴点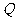 落在直线
落在直线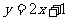 上.
上.
∴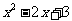 =
=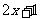 .
.
解得: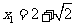 ,
,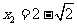 .
.
代入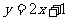 ,得
,得 ,
,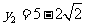 .
.
∴此时抛物线上存在点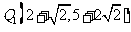 ,
,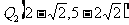
使△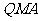 与△
与△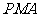 的面积相等. ………………………………(2分)
的面积相等. ………………………………(2分)
综上所述,抛物线上存在点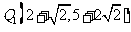 ,
,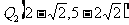
使△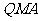 与△
与△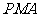 的面积相等.
的面积相等.
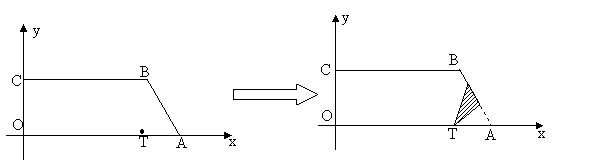
57(08浙江衢州)24、(本题14分)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8, ),C(0,
),C(0, ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;
(2)当纸片重叠部分的图形是四边形时,求t的取值范围;
(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。
(08浙江衢州24题解析)24、(本题14分)
解:(1) ∵A,B两点的坐标分别是A(10,0)和B(8, ),
),
∴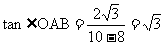 ,
,
∴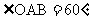
当点A´在线段AB上时,∵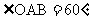 ,TA=TA´,
,TA=TA´,
∴△A´TA是等边三角形,且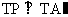 ,
,
∴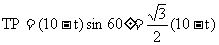 ,
,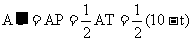 ,
,
|
|
|
 ∴
∴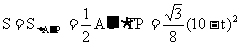 ,
,
|
|
|
|
|
|
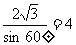 ,
,
|
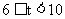 。
。
(2)当点A´在线段AB的延长线,且点P在线段AB(不与B重合)上时,
纸片重叠部分的图形是四边形(如图(1),其中E是TA´与CB的交点),
|
|
|
 当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A´与B重合时,T的坐标是(6,0)
|
|
|
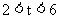 。
。
|
|
|
|
|
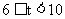 时,
时,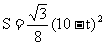 ,
,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是 。
。
2当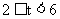 时,由图1,重叠部分的面积
时,由图1,重叠部分的面积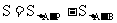
∵△A´EB的高是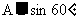 ,
,
∴
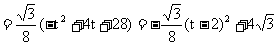
当t=2时,S的值最大是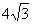 ;
;
3当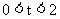 ,即当点A´和点P都在线段AB的延长线是(如图2,其中E是TA´与CB的交点,F是TP与CB的交点),
,即当点A´和点P都在线段AB的延长线是(如图2,其中E是TA´与CB的交点,F是TP与CB的交点),
∵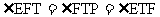 ,四边形ETAB是等腰形,∴EF=ET=AB=4,
,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴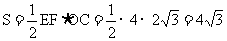
综上所述,S的最大值是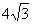 ,此时t的值是
,此时t的值是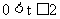 。
。
58(08浙江绍兴)24.将一矩形纸片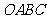 放在平面直角坐标系中,
放在平面直角坐标系中,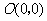 ,
,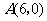 ,
,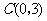 .动点
.动点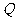 从点
从点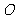 出发以每秒1个单位长的速度沿
出发以每秒1个单位长的速度沿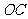 向终点
向终点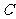 运动,运动
运动,运动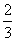 秒时,动点
秒时,动点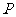 从点
从点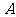 出发以相等的速度沿
出发以相等的速度沿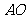 向终点
向终点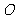 运动.当其中一点到达终点时,另一点也停止运动.设点
运动.当其中一点到达终点时,另一点也停止运动.设点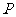 的运动时间为
的运动时间为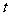 (秒).
(秒).
(1)用含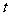 的代数式表示
的代数式表示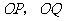 ;
;
(2)当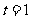 时,如图1,将
时,如图1,将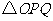 沿
沿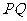 翻折,点
翻折,点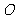 恰好落在
恰好落在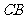 边上的点
边上的点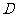 处,求点
处,求点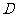 的坐标;
的坐标;
(3)连结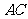 ,将
,将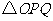 沿
沿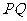 翻折,得到
翻折,得到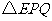 ,如图2.问:
,如图2.问: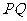 与
与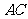 能否平行?
能否平行?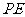 与
与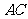 能否垂直?若能,求出相应的
能否垂直?若能,求出相应的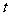 值;若不能,说明理由.
值;若不能,说明理由.

(08浙江绍兴24题解析)24.(本题满分14分)
解:(1)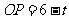 ,
,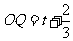 .
.

(2)当 时,过
时,过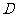 点作
点作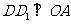 ,交
,交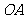 于
于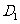 ,如图1,
,如图1,
则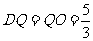 ,
,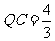 ,
,
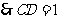 ,
,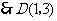 .
.
(3)①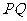 能与
能与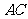 平行.
平行.
若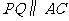 ,如图2,则
,如图2,则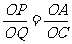 ,
,
即 ,
,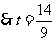 ,而
,而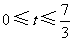 ,
,
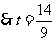 .
.
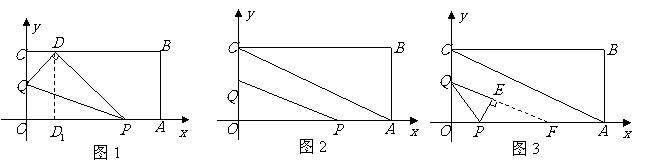
②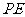 不能与
不能与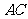 垂直.
垂直.
若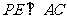 ,延长
,延长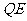 交
交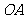 于
于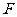 ,如图3,
,如图3,
则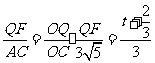 .
.
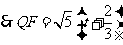 .
.
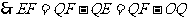
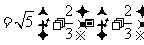
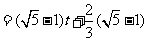 .
.
又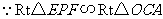 ,
,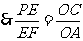 ,
,
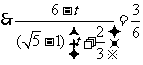 ,
,
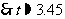 ,而
,而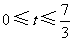 ,
,
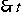 不存在.
不存在.
53.(08浙江淮安)(本题答案暂缺)28.(本小题14分)
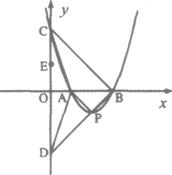
如图所示,在平面直角坐标系中.二次函数y=a(x-2)2-1图象的顶点为P,与x轴交点为 A、B,与y轴交点为C.连结BP并延长交y轴于点D.
(1)写出点P的坐标;
(2)连结AP,如果△APB为等腰直角三角形,求a的值及点C、D的坐标;
(3)在(2)的条件下,连结BC、AC、AD,点E(0,b)在线段CD(端点C、D除外)上,将△BCD绕点E逆时针方向旋转90°,得到一个新三角形.设该三角形与△ACD重叠部分的面积为S,根据不同情况,分别用含b的代数式表示S.选择其中一种情况给出解答过程,其它情况直接写出结果;判断当b为何值时,重叠部分的面积最大?写出最大值.
51.(08重庆市卷)(本题答案暂缺)28、(10分)已知:如图,抛物线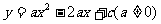 与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。
与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ。当△CQE的面积最大时,求点Q的坐标;
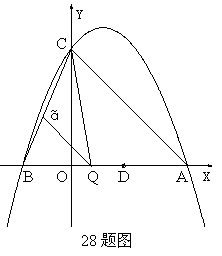 (3)若平行于x轴的动直线
(3)若平行于x轴的动直线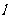 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0)。问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0)。问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
52(08浙江湖州)24.(本小题12分)
已知:在矩形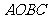 中,
中,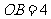 ,
,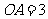 .分别以
.分别以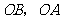 所在直线为
所在直线为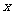 轴和
轴和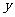 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.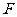 是边
是边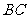 上的一个动点(不与
上的一个动点(不与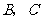 重合),过
重合),过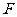 点的反比例函数
点的反比例函数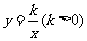 的图象与
的图象与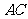 边交于点
边交于点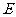 .
.
(1)求证: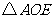 与
与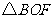 的面积相等;
的面积相等;
(2)记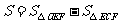 ,求当
,求当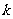 为何值时,
为何值时,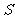 有最大值,最大值为多少?
有最大值,最大值为多少?
(3)请探索:是否存在这样的点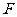 ,使得将
,使得将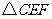 沿
沿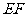 对折后,
对折后,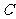 点恰好落在
点恰好落在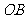 上?若存在,求出点
上?若存在,求出点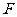 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(08浙江湖州24题解析)24.(本小题12分)
(1)证明:设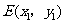 ,
,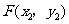 ,
,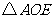 与
与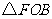 的面积分别为
的面积分别为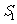 ,
,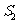 ,
,
由题意得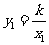 ,
,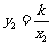 .
.
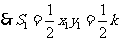 ,
,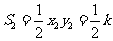 .
.
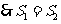 ,即
,即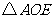 与
与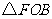 的面积相等.
的面积相等.
(2)由题意知: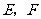 两点坐标分别为
两点坐标分别为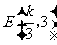 ,
,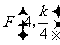 ,
,
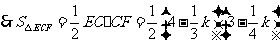 ,
,

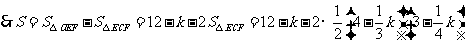
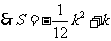 .
.
当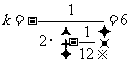 时,
时,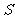 有最大值.
有最大值.
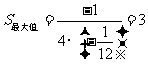 .
.
(3)解:设存在这样的点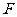 ,将
,将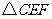 沿
沿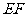 对折后,
对折后,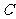 点恰好落在
点恰好落在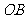 边上的
边上的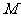 点,过点
点,过点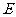 作
作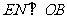 ,垂足为
,垂足为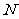 .
.
由题意得: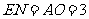 ,
,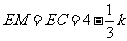 ,
,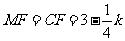 ,
,
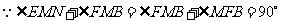 ,
,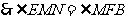 .
.
又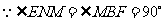 ,
,
 .
.
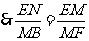 ,
,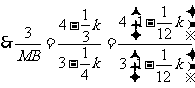 ,
,
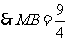 .
.
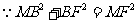 ,
,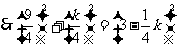 ,解得
,解得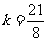 .
.
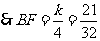 .
.
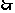 存在符合条件的点
存在符合条件的点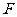 ,它的坐标为
,它的坐标为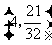 .
.
50.(08云南双柏)25.(本小题(1)-(3)问共12分;第(4)、(5)问为附加题10分,每小题5分,附加题得分可以记入总分,若记入总分后超过120分,则按120分记)
已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)求△ABC的面积;
(4)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(5)在(4)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
(08云南双柏25题解析)25.(本小题12分)解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
∴A、B、C三点的坐标分别是A(-6,0)、B(2,0)、C(0,8)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(-6,0)、B(2,0)代入表达式y=ax2+bx+8,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)∵AB=8,OC=8
∴S△ABC =×8×8=32
(4)依题意,AE=m,则BE=8-m,
∵OA=6,OC=8, ∴AC=10
∵EF∥AC ∴△BEF∽△BAC
∴= 即= ∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)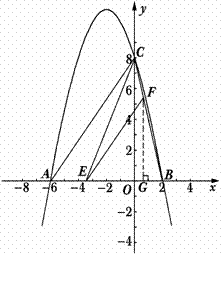
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(5)存在. 理由:
∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.
24.(08江苏扬州)(本题答案暂缺)26.(本题满分14分)
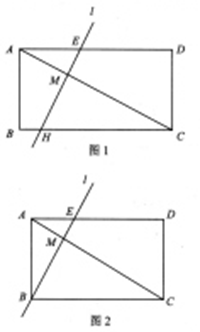
已知:矩形ABCD中,AB=1,点M在对角线AC上,直线l过点M且与AC垂直,与AD相交于点E。
(1)如果直线l与边BC相交于点H(如图1),AM=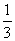 AC且AD=A,求AE的长;(用含a的代数式表示)
AC且AD=A,求AE的长;(用含a的代数式表示)
(2)在(1)中,又直线l 把矩形分成的两部分面积比为2:5,求a的值;
(3)若AM=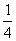 AC,且直线l经过点B(如图2),求AD的长;
AC,且直线l经过点B(如图2),求AD的长;
(4)如果直线l分别与边AD、AB相交于点E、F,AM=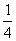 AC。设AD长为x,△AEF的面积为y,求y与x的函数关系式,并指出x的取值范围。(求x的取值范围可不写过程)
AC。设AD长为x,△AEF的面积为y,求y与x的函数关系式,并指出x的取值范围。(求x的取值范围可不写过程)
23.(08江苏盐城)(本题答案暂缺)28.(本题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ▲ ,数量关系为 ▲ .
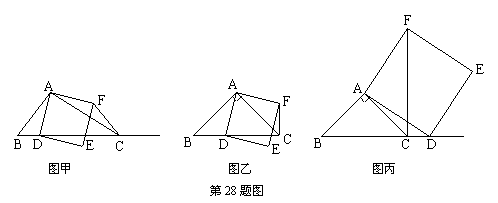 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC=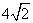 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
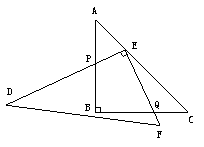
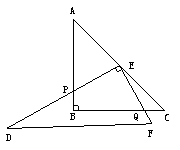
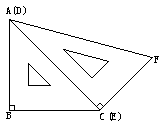
22.(08江苏徐州)(本题答案暂缺)28.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°
[操作]将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q
[探究一]在旋转过程中,
(1) 如图2,当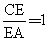 时,EP与EQ满足怎样的数量关系?并给出证明.
时,EP与EQ满足怎样的数量关系?并给出证明.
(2) 如图3,当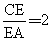 时EP与EQ满足怎样的数量关系?,并说明理由.
时EP与EQ满足怎样的数量关系?,并说明理由.
(3) 根据你对(1)、(2)的探究结果,试写出当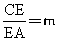 时,EP与EQ满足的数量关系式为_________,其中
时,EP与EQ满足的数量关系式为_________,其中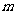 的取值范围是_______(直接写出结论,不必证明)
的取值范围是_______(直接写出结论,不必证明)
[探究二]若,AC=30cm,连续PQ,设△EPQ的面积为S(cm2),在旋转过程中:
(1) S是否存在最大值或最小值?若存在,求出最大值或最小值,若不存在,说明理由.
(2) 随着S取不同的值,对应△EPQ的个数有哪些变化?不出相应S值的取值范围.
21.(08江苏无锡)28.(本小题满分8分)
一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:
(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?
(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
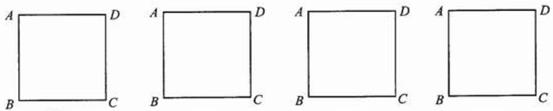
答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用)
|
|
|
|
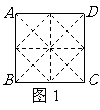
(08江苏无锡28题解析)28.解:(1)将图1中的正方形等分成如图的四个小正方形,将这4个转发装置安装在这4个小正方形对角线的交点处,此时,每个小正方形的对角线长为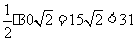 ,每个转发装置都能完全覆盖一个小正方形区域,故安装4个这种装置可以达到预设的要求.
,每个转发装置都能完全覆盖一个小正方形区域,故安装4个这种装置可以达到预设的要求.
················································································· (3分)(图案设计不唯一)
(2)将原正方形分割成如图2中的3个矩形,使得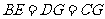 .将每个装置安装在这些矩形的对角线交点处,设
.将每个装置安装在这些矩形的对角线交点处,设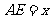 ,则
,则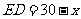 ,
,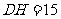 .
.
由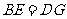 ,得
,得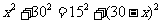 ,
,
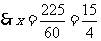 ,
,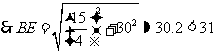 ,
,
即如此安装3个这种转发装置,也能达到预设要求.························· (6分)
或:将原正方形分割成如图2中的3个矩形,使得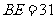 ,
,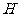 是
是 的中点,将每个装置安装在这些矩形的对角线交点处,则
的中点,将每个装置安装在这些矩形的对角线交点处,则 ,
,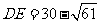 ,
, 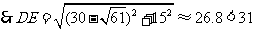 ,即如此安装三个这个转发装置,能达到预设要求.········································ (6分)
,即如此安装三个这个转发装置,能达到预设要求.········································ (6分)
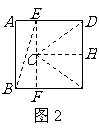
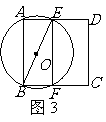
要用两个圆覆盖一个正方形,则一个圆至少要经过正方形相邻两个顶点.如图3,用一个直径为31的 去覆盖边长为30的正方形
去覆盖边长为30的正方形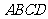 ,设
,设 经过
经过 ,
, 与
与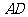 交于
交于 ,连
,连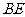 ,则
,则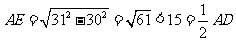 ,这说明用两个直径都为31的圆不能完全覆盖正方形
,这说明用两个直径都为31的圆不能完全覆盖正方形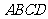 .
.
所以,至少要安装3个这种转发装置,才能达到预设要求.············· (8分)
评分说明:示意图(图1、图2、图3)每个图1分.
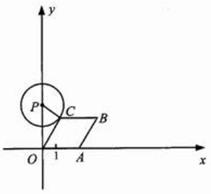
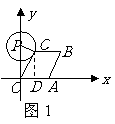
20.(08江苏无锡)27.(本小题满分10分)
如图,已知点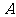 从
从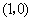 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿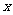 轴向正方向运动,以
轴向正方向运动,以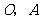 为顶点作菱形
为顶点作菱形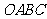 ,使点
,使点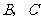 在第一象限内,且
在第一象限内,且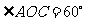 ;以
;以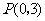 为圆心,
为圆心,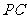 为半径作圆.设点
为半径作圆.设点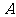 运动了
运动了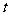 秒,求:
秒,求:
(1)点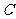 的坐标(用含
的坐标(用含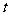 的代数式表示);
的代数式表示);
(2)当点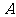 在运动过程中,所有使
在运动过程中,所有使 与菱形
与菱形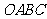 的边所在直线相切的
的边所在直线相切的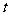 的值.
的值.
(08江苏无锡27题解析)27.解:(1)过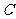 作
作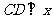 轴于
轴于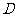 ,
,
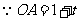 ,
,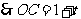 ,
,
 ,
,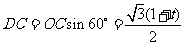 ,
,
 点
点 的坐标为
的坐标为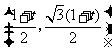 .··· (2分)
.··· (2分)
 (2)①当
(2)①当 与
与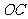 相切时(如图1),切点为
相切时(如图1),切点为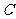 ,此时
,此时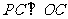 ,
,
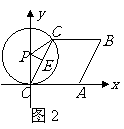
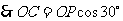 ,
,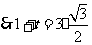 ,
,
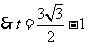 .··········· (4分)
.··········· (4分)
②当 与
与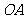 ,即与
,即与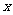 轴相切时(如图2),则切点为
轴相切时(如图2),则切点为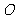 ,
,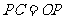 ,
,
过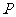 作
作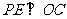 于
于 ,则
,则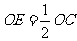 ,················································· (5分)
,················································· (5分)
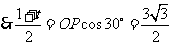 ,
,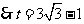 .············································· (7分)
.············································· (7分)
③当 与
与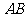 所在直线相切时(如图3),设切点为
所在直线相切时(如图3),设切点为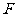 ,
,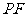 交
交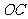 于
于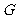 ,
,
则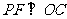 ,
,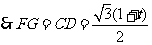 ,
,
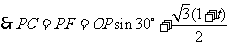 .························································ (8分)
.························································ (8分)
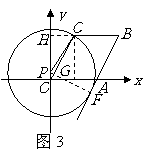 过
过 作
作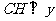 轴于
轴于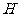 ,则
,则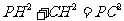 ,
,
 ,
,
化简,得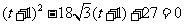 ,
,
解得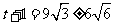 ,
,
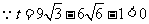 ,
,
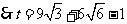 .
.
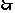 所求
所求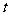 的值是
的值是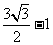 ,
,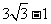 和
和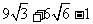 .···························· (10分)
.···························· (10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com