
熟练地解决方程与不等式相关的问题
通过对方程与不等式基础知识的复习,解决中考中常见的问题。
方程与不等式
25.(1)DF = DM.
(2)仍具有(1)的结论,即DF = DM.
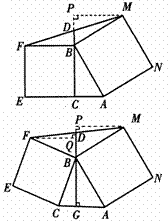
证明:延长CD,过M作MP⊥CD,交于P,P为垂足.
∵ ∠MBP +∠ABC = 90°,∠BAC +∠ABC = 90°,
∴ ∠MBP =∠BAC.
又 ∠ACB =∠MPB = 90°,AB = BM,
∴ △ABC≌△BMP,从而 BC = MP.
∵ BC = BF, ∴ BF = MP.
又 ∠PDM =∠BDF,∠DPM =∠DBF,
∴ △DBF≌△DPM, ∴ DF = DM.
(3)高.
证明:如图,延长GD,过M、F作GD的垂线垂足为P、Q.
∵ ∠MBP +∠BMP = 90°,∠ABG +∠MBP = 90°, ∴∠BMP =∠ABG.
又 ∠MPB =∠AGB = 90°,AB = BM, ∴ △ABG≌△BMP, ∴ MP = BG.
同理 △FQB≌△BGC, ∴ FQ = BG,∴ MP = FQ.
∵ ∠FDQ =∠MDP,∠FQD =∠MPD = 90°,∴ △FDQ≌△MDP,进而 DF = DM.
说明 过F作FH∥BM交BD的延长线于H.通过证明△ABC≌△HFB得HF = AB = BM,进而证明△BDM≌△HFD,得出D是FM的中点.
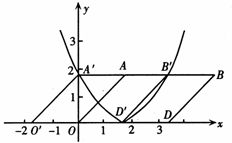
24.(1)作出平移后的四边形A′B′D′O′如右.顶点坐标分别为A′(0, )、B′(2
)、B′(2 ,
, )、D′(
)、D′( ,0)、O′(-
,0)、O′(- ,0).
,0).
(2)由题意可设抛物线C的解析式为 y = ax2
+ bx + ,
,
则 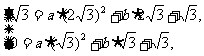 解得 a =
解得 a =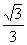 ,b =-2.
,b =-2.
 ∴ 抛物线C的解析式为 y =
∴ 抛物线C的解析式为 y =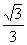 x2-2x +
x2-2x + .
.
∵ 四边形A′B′D′O′是平行四边形,
∴ 它的面积为O′D′×OA′ = 2 ×
× = 6.
= 6.
假设存在点P,则△ABP的面积为3.
设△ABP的高为h,则 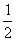 ×AB×h =
×AB×h =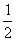 ×2
×2 ×h
= 3,得 h
=
×h
= 3,得 h
= .
.
即点P到AB的距离为 ,∴ P点的纵坐标为0或2
,∴ P点的纵坐标为0或2 .
.
∴ 当P的纵坐标为0时,即有 0 =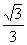 x2-2x +
x2-2x + ,解得
x1 = x2 =
,解得
x1 = x2 = .
.
当P的纵坐标为2 时,即有 2
时,即有 2 =
=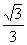 x2-2x +
x2-2x + ,解得
,解得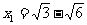 ,
,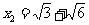 .
.
因此存在满足条件的点P,坐标为( ,0),(
,0),( ,2
,2 ),(
),(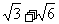 ,2
,2 ).
).
23.(1)△OBD∽△PAD.
证明 ∵ PA、PB是⊙O的切线,∴ OA⊥PA,OB⊥PB,∴ ∠OAP =∠OBD = 90°.
又∠D =∠D,∴ △OBD∽△PAD.
(2) ∵ ∠P = 45°, ∴ ∠DOB = 45°,∴ △OBD、△PAD均是等腰直角三角形,
从而
PD =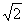 PA,BD = OB.
PA,BD = OB.
又 ∵ PA = 2 +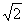 ,PA = PB,
,PA = PB,
∴ BD = OB
= PD-PB =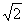 PA-PA=(
PA-PA=(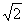 -1)PA=(
-1)PA=(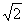 -1)(2+
-1)(2+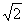 )=
)=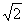 .
.
故
S阴影 = S△OBD-S扇形 =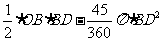 =
=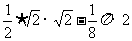 =
=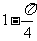 .
.
22.(1)设第一批购入的衬衫单价为x元/件,则
|
|
第一批 |
第二批 |
|
单价 |
x |
x + 4 |
|
总价 |
80000 |
176000 |
|
数量 |
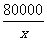 |
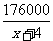 |
有 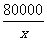 ×2 =
×2 =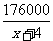 .解得 x = 40,此即为第一批购入衬衫的单价.
.解得 x = 40,此即为第一批购入衬衫的单价.
(2)由(1)知,第一批购入了 80000 ÷ 40 = 2000件.
在这两笔生意中,华联商场共赢利为
2000×(58-40)+(2000×2-150)×(58-44)+ 150×(58×0.8-44)= 90260元.
答:第一批购入这种衬衫的单价为40元,两笔生意中华联商场共赢利90260元.
21.(1)∵ 20 ÷ 10% = 200, ∴ 这天共借了200本.
|
类别 |
少儿类 |
科技类 |
文艺类 |
体育类 |
其他 |
|
数量(本) |
20 |
50 |
80 |
40 |
10 |
|
比例 |
10% |
25% |
40% |
20% |
5% |
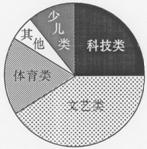 (2)最好选用扇形统计图,图如右:
(2)最好选用扇形统计图,图如右:
(3)建议:可多采购些文艺类书籍.
20.(1)∵ 反比例函数的图象有一支在第一象限,∴ m-5>0,即 m>5.
因此 m的取值范围为m>5.
(2)由题意可知,反比例函数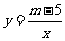 的图象经过点(2,2),
的图象经过点(2,2),
∴ 2×2 = m-5,得 m = 9,∴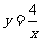 .
.
当x =-2时,y =-2;当x =-1时,y =-4.
故根据反比例函数图象知,当-2<x<-1时,y的取值范围是-4<x<-2.
19.(1)原式=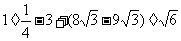 =
=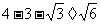 =
=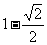 .
.
(2)原式=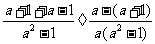 =
=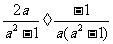 =-2a2.
=-2a2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com