(三)实践探索,归纳新知

在同一直角坐标系内分别作出下列一次函数的图象：

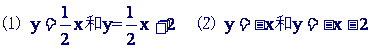
这两个函数的图象是什么形状？讨论它们之间有什么关系？

[学生活动]

1、分组探究。

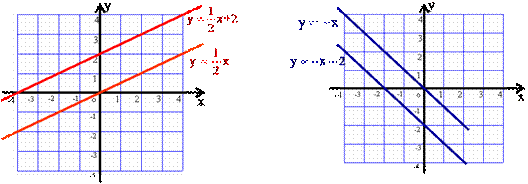学生画出函数的图象后，教师展示两位学生画的图象，教师进行引导，让学生观察归纳。然后由特殊推广到一般，总结直线y=kx+b和y=kx之间的关系。

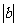一次函数y=kx+b的图象是一条直线，称为直线y=kx+b，它可以看作是由直线y=kx平移 个单位长度得到的(当b＞0时，向上平移；当b＜0时，向下平移)。

2、思考探索

既然一次函数的图象可由正比例函数的图象平移得到，我们要再画一次函数的图象，除了描点法之外，还有其它的方法吗？如： y=2x+1

在学生充分商讨之后，发表自已的见解，在学生回答的基础上总结出平移法与两点法。

3、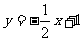动手操作

例：画出函数y=2x+3和的图象.

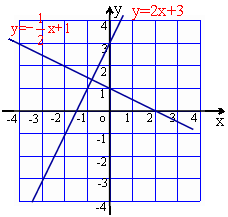
4、观察总结

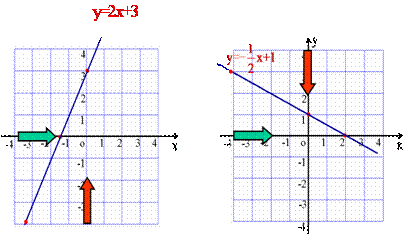
出示课件，进行动画演示，通过动画让学生从视觉上感受y与x的变化关系. 在此基础上让学生总结出一次函数的性质：

当k﹥0时，y随x的增大而增大，

当k＜0时，y随x的增大而减小。

(二)引入新课

既然正比例函数是特殊的一次函数，那么一次函数的图象是什么形状呢？它和正比例函数图象之间有什么关系呢？下面我们就来共同研究。

板书课题：一次函数(二)

(一)提出问题，创设情景

1.什么是正比例函数？它的图象和性质是什么？

2.什么是一次函数？它和正比例函数之间有什么关系？

重点：一次函数的图象和性质

难点：由一次函数的图象归纳得出一次函数的性质及对性质的理解三、教学过程

4、情感态度

(1)通过画函数的图象，并借助图象研究函数的性质，体验数与形的内在联系，感受函数图象的简洁美。

(2)在探究一次函数的图象和性质的活动中，通过一系列富有探究性的问题，渗透与他人交流、合作的意识和探究精神。

3、解决问题

通过一次函数图象和性质的研究，体会数形结合法在问题解决中的作用，并能运用性质、图象及数形结合法解决相关函数问题。

2、数学思考

(1)通过对应描点来研究一次函数的图象，经历知识的归纳、探究过程。

(2)通过一次函数的图象归纳函数的性质，体验数形结合法的应用。

1、知识技能

(1)理解直线y=kx+b与直线y=kx之间的的位置关系。

(2)会用恰当的方法画出一次函数的图象。

(3)掌握一次函数的性质。

5、用四块如图(1)所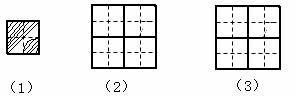示的瓷

砖拼铺一个成正方形的地板，使拼

铺的图案成中心对称图形，请你在

图(2)、图(3)中各画出一种拼

法。(要求：两种拼法各不相同，

4、试用两个圆，两条平行线设计一些具有旋转关系的图案，并说明你的设计意图。