
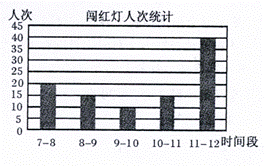
8. 一交通管理人员星期天在市中心的某十字路口,对闯红灯的人次进行统计,根据上午7∶00 ~ 12∶00中各时间段(以1小时为一个时间段)闯红灯的人次,制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别为
(A)15,15 (B)10,15 (C)15,20 (D)10,20
[参考答案]A
[解析]本题考查数的代表,考查学生读图的能力,从图中可以读出:20,15,10,15,40这组数,15出现了两次,是众数,由小到大排一下为:10,15,15,20,40,15排在中间,所以中位数应该是15。本题应选A。
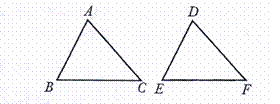
7. 如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是
(A)∠B=∠E,BC=EF (B)BC=EF,AC=DF
(C)∠A=∠D,∠B=∠E (D)∠A=∠D,BC=EF
[参考答案]D
[解析]本题考查三角形全等的知识,A是两边夹角对应相等,B是三边对应相等,C是两角夹边,D是边边角对应相等,所以D这一组不能使两三角形全等。
6. 在函数y=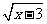 中,自变量x的取值范围是
中,自变量x的取值范围是
(A)x≥ - 3 (B)x≤ - 3 (C)x≥ 3 (D )x≤ 3
[参考答案]C
[解析]本题考查函数自变量的取值范围。本是是一个根式,被开方数是一个非负数,即
x-3≥0,解这个不等式,可得x≥3,本题应选C。
5. 下列事件是必然事件的是
(A)打开电视机,任选一个频道,屏幕上正在播放天气预报
(B)到电影院任意买一张电影票,座位号是奇数
(C)在地球上,抛出去的篮球会下落
(D)掷一枚均匀的骰子,骰子停止转动后偶数点朝上
[参考答案]C
[解析]本题考查学生概率的知识,事件有随机事件、必然事件和不可能事件,A、B、D是偶然事件,C是自然现象,属必然事件。
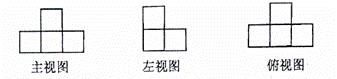
4. 用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是
(A)4 (B)5 (C)6 (D)7
[参考答案]B
[解析]本题考查三视图的知识,考查学生空间想象能力。本题可在俯视图上注明每一个小方块叠加的块数,如下图,这样能准确计算出小正体的个数。
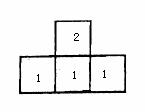
所以一共有5个。
3. 北京奥运会火炬传递以“和谐之旅”为主题,以“点燃激情 传递梦想”为口号进行,其传递总路程约为1370000千米,这个路程用科学计数法表示为
(A)13.7×104千米 (B)13.7×105千米
(C)1.37×105千米 (D)1.37×106千米
[参考答案]D
[解析]本题考查学生对科学记数法的掌握,A、B前面的部分大于10,不符合要求,要求前面的部分是大于或等于1,而小于10,小数点向左移动了6位,应该选D。要注意如果小数点向右移动,则记成10负整数次幂。
2. 化简( - 3x2)·2x3的结果是
(A)- 6x5 (B)- 3x5 (C)2x5 (D)6x5
[参考答案]A
[解析]本题考查单项式的乘法以及幂的运算,先把它的系数相乘得-6,再把同底数的幂相乘得x5,结果为- 6 x5,本题注意同底数的幂相乘时,指数相加,不是相乘,异号两数相乘,得负。
1. 2cos45°的值等于
(A)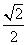 (B)
(B)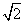 (C)
(C)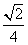 (D)
(D)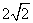
[参考答案]B
[解析]本题考查学生特殊三角函数值的知识。可以通过定义来求或是表格来记忆30º、45º、60º的正弦、余弦和正切值。
24、(2004年深圳南山区)如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交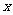 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线
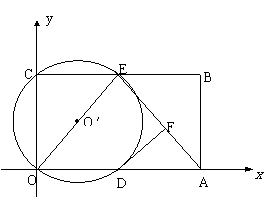 BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
3.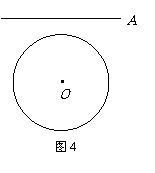 若OA所在的直线向上平移且与⊙O无公共点,请你根
若OA所在的直线向上平移且与⊙O无公共点,请你根
据原题中的条件完成图4,并判断结论是否还成立?
(只需交待判断)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com