24. 如果m是从0，1，2，3四个数中任取的一个数，n是从0，1，2三个数中任取的一个数，那么关于x的一元二次方程x² – 2mx + n² = 0有实数根的概率为　　　　　　　 .

[参考答案]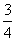

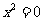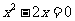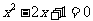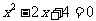[解析]本题考查概率与一元二次方程根的判别式的知识，首先要求写出所有的一元二次方程，m=0时，n或取0，1，3，有三个方程，,,,第一个方程有实数根，当m=1时，有三个方程：，，，前两个方程有实数根；当m=2时，有三个方程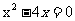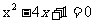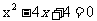：，，这三个方程都有实数根；当m=3时，有三个方程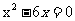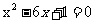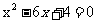：，，这三个方程都有实数根，一共是12个方程，有9个有实数根，所以有实数根的概率为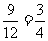

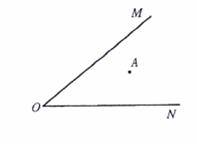
23. 如图，已知点A是锐角∠MON内的一点，试分别在OM、ON上确定点B、点C，使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点　　　　　　　　　　　　　

　　　　　　　　　　　　 (要求画出草图，保留作图痕迹)

[参考答案]．分别作点A关于OM、ON的对称点A’和A’’；连结A’A’’分别交OM、ON于点曰、点C，则点B、点C即为所求(2分)如图所示(2分)；

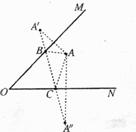
[解析]本题考查的是最短的问题，要求学生会应用转化的思想把三角形的周长转化到一条直线上来，手段就是作出A点关于OM、ON的对称点，也就是利用轴对称变换，再运用两点之间线段最短，从而使问题得以解决。

22. 某农场租用播种机播种小麦，在甲播种机播种2天后，又调来乙播种机参与播种，直至完成800亩的播种任务，播种亩数与天数之间的函数关系如图所示，那么乙播种机参与播种的天数是　　　　 　.

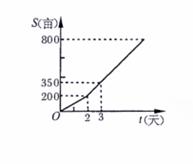
[参考答案]4

[解析]本题考查学生一次函数的应用，题中的函数有正比例函数以及一次函数，能过两点确定一条直线以及知道函数上点的纵坐标求横坐标。设一次函数的解析式为y=kx+b,它经过点(2，200)，(3，350)，可求得函数的表达式为：y=150x-100,当y=800时，x=6,所以乙参加了4天。

21. 已知y = 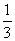x – 1,那么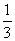x² – 2xy + 3y² – 2的值是　　　　　　 .

[参考答案]1

[解析]本题考查求代数式的运算，涉及到消元的思想以及整式的运算。可以把y = 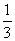x – 1直接代入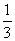x² – 2xy + 3y² – 2，得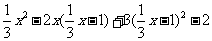

==1

14. 如图，在平面直角坐标系中，△PQR是△ABC经过某种变换后得到的图形，观察点A与点P，点B与点Q，点C与点R的坐标之间的关系.在这种变换下，如果△ABC中任意一点M的坐标为(x，y)，那么它们的对应点N的坐标是　　　　　 .

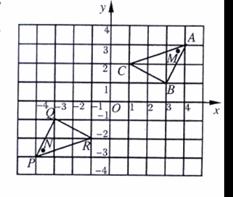
[参考答案](-x,-y)

[解析]本题考查图形变换之一-----中心对称，也考查了数形结合的思想，即从点的坐标判断图形的变换。从坐标系中可能读出对应点的坐标互为相反数，说明它们关于原点对称，从而归纳出关于原点对称的点它们的横坐标、纵坐标都互为相反数，所以M(x，y)的对称点为(-x，-y).

B　 卷

13. 如图，已知PA是⊙O的切线，切点为A，PA = 3，∠APO = 30°，那么OP =　　　　 .

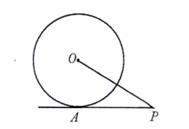
[参考答案]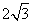

[解析]本题考查圆的切线的性质以及三角形函数的知识。凡是切线一般都得连过切点的半径。本题应先连结OA，得直角三角形OAP，根据解直角三角形的知识，。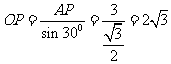

12. 已知x = 1是关于x的一元二次方程2x² + kx – 1 = 0的一个根，则实数k的值是　　　 .

[参考答案]-1

[解析]本题考查一元二次方程根的概念及一元一次方程的解法，把x=1代入方程得：

2+k-1=0，解得k=-1,本题应填-1。

将答案直接写在该题目中的横线上.

11. 现有甲、乙两支排球队，每支球队队员身高的平均数均为1.85米，方差分别为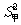=0.32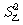，=0.26，则身高较整齐的球队是　　　　 队.

[参考答案]乙

[解析]本题考查数据的方差，方差是衡量一组数据波动大小的量，方差越小，其波动就越小。由于0.26<0.32，所以身高较整齐的球队是乙队。

10. 有下列函数：①y = - 3x；②y = x – 1：③y = - 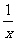　(x < 0)；④y = x² + 2x + 1.其中当x在各自的自变量取值范围内取值时，y随着x的增大而增大的函数有

(A)①②　　　　　　 (B)①④　　　　　　 (C)②③　　　　　　 (D)③④

[参考答案]C

[解析]本题考查函数的增减性，对于函数y = - 3x，由于-3<0，y随x的增大而减少；函数y = x – 1，k=1 >0，y随x的增大而增加，y = - 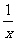　(x < 0)，由于k=-1，当x<0时，y随x的增大而增加；y = x² + 2x + 1是二次函数，其增减性要分在对称轴的左侧还是在对称轴的右侧。所以本题应选C。

第Ⅱ卷(非选择题，共70分)

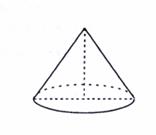
9. 如图，小红同学要用纸板制作一个高4cm，底面周长是6πcm的圆锥形漏斗模型，若不计接缝和损耗，则她所需纸板的面积是

(A)12πcm²　　　　　　 (B)15πcm²　　　　　　 (C)18πcm²　　　　　　 (D)24πcm²

[参考答案]B

[解析]本题考查圆锥侧面展开图的知识，圆锥的侧面展开图是扇形，面积为底面圆的周长与母线的积的一半，底圆圆的周长为6π，则它的半径为3cm，高为4cm，则母线长m由勾股定理可得5cm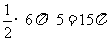，，本题应先B