
28. 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且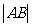 =3
=3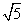 ,sin∠OAB=
,sin∠OAB=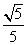 .
.
(1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的函数表达式;
(2)在(1)中,抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若将点O、点A分别变换为点Q( -2k ,0)、点R(5k,0)(k>1的常数),设过Q、R两点,且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N,其顶点为M,记△QNM的面积为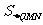 ,△QNR的面积
,△QNR的面积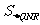 ,求
,求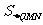 ∶
∶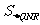 的值.
的值.
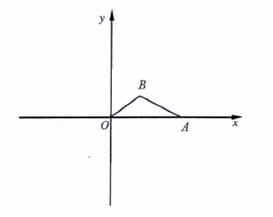
解:(1)如图,过点B作BD⊥OA于点D.
在Rt△ABD中,
∵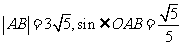
∴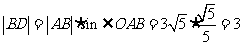
又由勾股定理,得
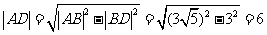
∴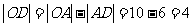
∵点B在第一象限内,
∴点B的坐标为(4,3)。
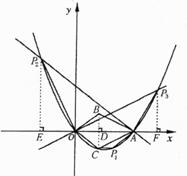
∴点B关于x轴对称的点C的坐标为(4,-3). ……2分
设经过O(0,O)、C(4,-3)、A(10,0)三点的抛物线的函数表达式为
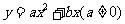 .
.
由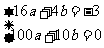 解得
解得
∴经过O、C、A三点的抛物线的函数表达式为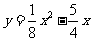 . ……2分
. ……2分
(2)假设在(1)中的抛物线上存在点P,使以P、O、C、A为顶点的四边形为梯形.
①∵点C(4,-3)不是抛物线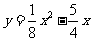 的顶点,
的顶点,
∴过点C作直线OA的平行线与抛物线交于点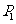 .
.
则直线C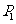 的函数表达式为y=-3.
的函数表达式为y=-3.
对于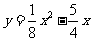 ,令y=-3解得x=4或x=6
,令y=-3解得x=4或x=6
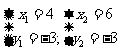
而点C(4,3),∴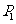 (6,-3).
(6,-3).
在四边形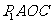 中,
中,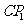 ∥
∥ ,显然
,显然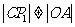 .
.
∴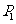 (6,-3)是符合要求的点. ……1分
(6,-3)是符合要求的点. ……1分
②若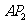 ∥CO.设直线CO的函数表达式为
∥CO.设直线CO的函数表达式为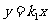 ,
,
将点c(4,-3)代入,得4k1=-3.∴k1=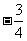
∴直线CO的函数表达式为y=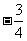 x
x
于是可设直线AP2的函数表达式为y=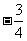 x+b1.
x+b1.
将点A(10,O)代人,得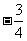 ×l0+b1=0.∴b1=
×l0+b1=0.∴b1=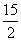 .
.
∴直线AP2的函数表达式为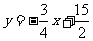
解方程组 得
得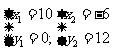
而点A(10,O),∴P2(-6,12).
过点P2作P2E⊥x轴于点E,则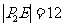 .
.
在Rt△AP2E中,由勾股定理,得
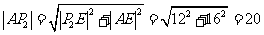
而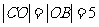
在四边形P20CA中,AP2∥CO,但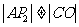
∴点P2(-6,12)是符合要求的点. ……1分
③若OP3∥CA.设直线CA的函数表达式为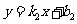 ,
,
将点A(10,0)、C(4,-3)代入,
得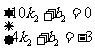 ,解得
,解得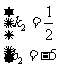
∴直线CA的函数表达式为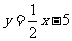
∴直线AP3的函数表达式为y=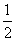 x
x
解方程组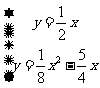 得
得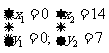
而点O(0,O),∴P3(14,7).
过点P3作P3E⊥x轴于点F,则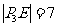 .
.
在Rt△AP3F中,由勾股定理,得
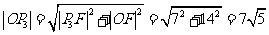
而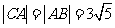
在四边形P30CA中,OP3∥CA,但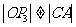
∴点P3(14,7)是符合要求的点. ……1分
综上可知,在(1)中的抛物线上存在点P1 (6,-3)、P2(-6,12)、P3(14,7),
使以P、O、C、,A为顶点的四边形为梯形. ……1分
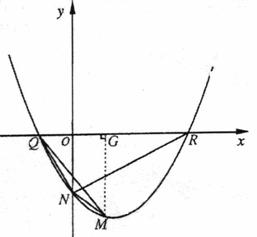
(3)由题知.抛物线的开口可能向上,也可能向下
①当抛物线开口向上时,则此抛物线与y的负半轴交于点N
设抛物线的函数表达式为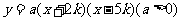
即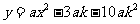
=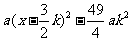
如图,过点M作MG⊥x轴于点G.
∵Q(-2k,O)、R(5k,O)、G(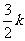 ,0)、N(0,-10ak2)、M(
,0)、N(0,-10ak2)、M(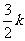 ,
,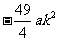 )
)
∴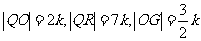
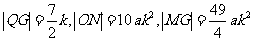
∴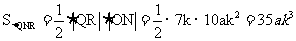
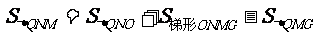
=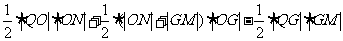
=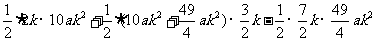
=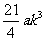
∴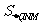 :
: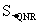 =
=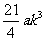 :
: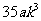 =3:20 …2分
=3:20 …2分
②当抛物线开口向下时,则此抛物线与y轴的正半轴交于点N
同理,可得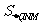 :
: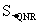 =3:20 ……1分
=3:20 ……1分
综上可知, 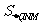 :
: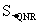 的值为3:20
……1分
的值为3:20
……1分
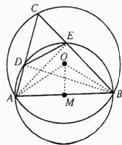
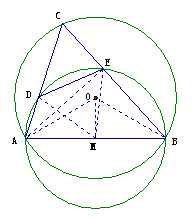
27. 如图,已知⊙O的半径为2,以⊙O的弦AB为直径作⊙M,点C是⊙O优弧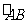 上的一个动点(不与点A、点B重合).连结AC、BC,分别与⊙M相交于点D、点E,连结DE.若AB=2
上的一个动点(不与点A、点B重合).连结AC、BC,分别与⊙M相交于点D、点E,连结DE.若AB=2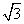 .
.
(1)求∠C的度数;
(2)求DE的长;
(3)如果记tan∠ABC=y,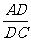 =x(0<x<3),那么在点C的运动过程中,试用含x的代数式表示y.
=x(0<x<3),那么在点C的运动过程中,试用含x的代数式表示y.
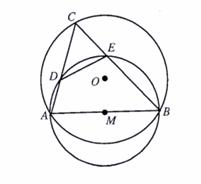
解:(1)连结OB、OM.
则在Rt△OMB中,
∵OB=2,MB=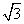 ,
,
∴OM=1.
∵OM=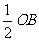 ,∴∠OBM=30。.
,∴∠OBM=30。.
∴∠MOB=60º.
连结OA.则∠AOB=120º.
∴∠C=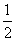 ∠AOB=60º. ……3分
∠AOB=60º. ……3分
(2)连结AE,则∠AEB=90º
∵∠c=60º,∠CAE=30º
∠DME=2∠CAE=60º
∵MD=ME,∴△MDE为等边三角形
∴DE=ME=BM= ……3分
……3分
(3)
由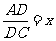 ,可得AD=x·DC,AC=AD+DC=(x+1)·DC
,可得AD=x·DC,AC=AD+DC=(x+1)·DC
在Rt△ACE中,
CE=ACcos∠ACE=(x+1)·DC·cos60º=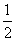 (x+1)·DC;
(x+1)·DC;
AE=AC·sin∠ACE=(x+1)·DC·sin60º=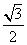 (x+1)·DC.
(x+1)·DC.
连结BD,直角三角形BDC,∠DBC=30º,BC=2CD
∴BE=BC-CE=2DC-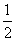 (x+1)·DC=
(x+1)·DC= 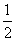 (3-x)·DC. …3分
(3-x)·DC. …3分
在Rt△ABE中,
∵tan∠ABC=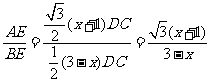
∴y=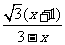 (0<x<3). …1分
(0<x<3). …1分
26. 金泉街道改建工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的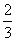 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为0.84万元,乙队每天的施工费用为0.56万元.工程预算的施工费用为50万元.为缩短工期以减少对住户的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要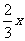 天.
天.
根据题意,得
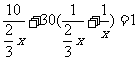
解得x=90.
经检验,x=90是原方程的根. ……3分
∴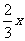 =
=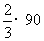 =60
=60
答:甲、乙两队单独完成这项工程各需要60天和90天. ……1分
(2)设甲、乙两队合作完成这项工程需要y天.则有
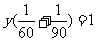
解得y=36. ……2分
需要施工费用:36×(O.84+O.56)=50.4(万元). ……1分
∵50.4>50,工程预算的施工费不够用,需追加预算O.4万元. ……1分
20. 已知:在梯形ABCD中,AD∥BC,AB = DC,E、F分别是AB和BC边上的点.
(1)如图①,以EF为对称轴翻折梯形ABCD,使点B与点D重合,且DF⊥BC.若AD =4,BC=8,求梯形ABCD的面积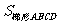 的值;
的值;
(2)如图②,连接EF并延长与DC的延长线交于点G,如果FG=k·EF(k为正数),试猜想BE与CG有何数量关系?写出你的结论并证明之.

解(1)解:由题意,有△BEF≌△DEF。
∴BF=DF. …………………1分
如图,过点A作AG⊥BC于G
则四边形AGFD是矩形.
∴AG=DF,GF=AD=4
在Rt△ABG和Rt△DCF中,
∵AB=DC,AG=DF,
∴Rt△ABG≌ Rt△DCF
∴BG=CF …………………2分
∴BG=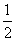 (BC-GF)=
(BC-GF)=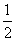 (8-4)=2
(8-4)=2
∴DF=BF=BG+GF=2+4=6 …………………2分
∴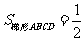 (AD+BC)
(AD+BC)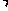 DF=
DF=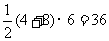 …………………1分
…………………1分

(2)猜想:CG=k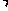 BE(或BE=
BE(或BE=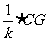 )
…………………1分
)
…………………1分
证明:如图,过点E作EH∥CG,交BC于点H.
则∠FEH=∠FGC,
又∠EFH=∠GFC,
∴△EFH∽△GFC,
∵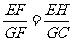
而FG=k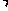 EF,即
EF,即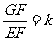
∴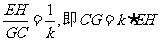 …………………2分
…………………2分
∵EH∥CG,∴∠EHB=∠DCB
而ABCD是等腰梯形,∴∠B=∠DCB
∴∠B=∠EHB,∠BE=EH
∴CG=k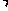 BE
…………………1分
BE
…………………1分
B卷
19. 一不透明纸箱中装有形状、大小、质地等完全相同的4个小球,分别标有数字1,2,3,4.
(1)从纸箱中随机地一次取出两个小球,求这两个小球上所标的数字一个是奇数另一个是偶数的概率;
(2)先从纸箱中随机地取出一个小球,用小球上所标的数字作为十位上的数字;将取出的小球放回后,再随机地取出一个小球,用小球上所标的数字作为个位上的数字,则组成的两位数恰好能被3整除的概率是多少?试用树状图或列表法加以说明.
解:(1)从纸箱中随机地一次取出两个小球,所标数字的所有可能结果有:
(1,2)、(1,3)、(1,4)、(2,3)、(2,4)、(3,4),共6种;
而所标数字一个是奇数另一个是偶数的有4种。 …………………3分
∴P=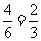 …………………2分
…………………2分
(2)画树状图:
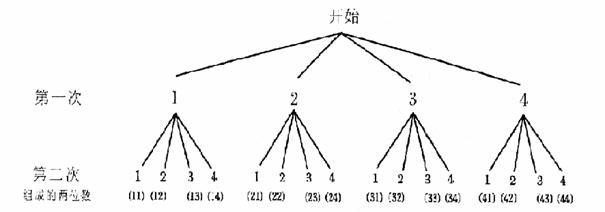
 或用列表示:
或用列表示:
|
1 |
2 |
3 |
4 |
||
|
1 |
(11) |
(12) |
(13) |
(14) |
||
|
2 |
(21) |
(22) |
(23) |
(24) |
||
|
3 |
(31) |
(32) |
(33) |
(34) |
||
|
4 |
(41) |
(42) |
(43) |
(44) |
…………………3分
所有可能出现的结果共有16种,其中能被3整除的有5种
∴P=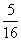 …………………2分
…………………2分
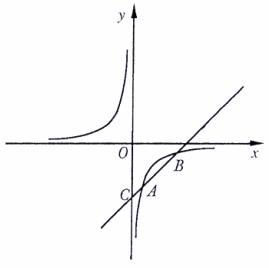
18. 如图,已知反比例函数y = 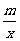 的图象经过点A(1,- 3),一次函数y = kx + b的图象经过点A与点C(0,- 4),且与反比例函数的图象相交于另一点B.
的图象经过点A(1,- 3),一次函数y = kx + b的图象经过点A与点C(0,- 4),且与反比例函数的图象相交于另一点B.
(1)试确定这两个函数的表达式;
(2)求点B的坐标.
解:(1)∵反比例函数y = 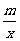 的图象经过点A(1,- 3)
的图象经过点A(1,- 3)
∴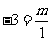 ,即m=-3
,即m=-3
∴反比例函数的表达式为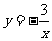 …………………3分
…………………3分
∵次函数y = kx + b的图象经过点A1,- 3)、C(0,- 4)
∴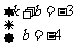 解得
解得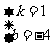
∴一次函数的表达式为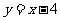 …………………3分
…………………3分
(2)由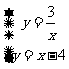 消去y,得
消去y,得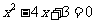
解得x=1或x=3
可得y=-3或y=-1.
于是点A的坐标为(1,-3)点B的坐标为(3,-1)…………………2分
17. 如图,某中学九年级一班数学课外活动小组利用周末开展课外实践活动,他们要在某公园人工湖旁的小山AB上,测量湖中两个小岛C、D间的距离.从山顶A处测得湖中小岛C的俯角为60°,测得湖中小岛D的俯角为45°.已知小山AB的高为180米,求小岛C、D间的距离.(计算过程和结果均不取近似值)
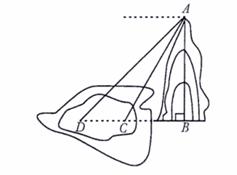
解:如图,由已知,可得
∠ACB=60º,∠ADB=45º,
∴在Rt△ABD中 ,BD=AB …………………2分
∵tan60º=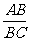 ,
,
∴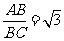 ,即BC=
,即BC=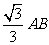
∵BD=BC+CD,∴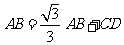 …………………3分
…………………3分
∴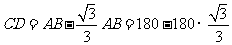
=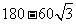 (米)
…………………2分
(米)
…………………2分
答:小岛C、D间的距离.为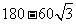 米 …………………1分
米 …………………1分
16. 解不等式组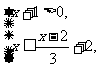 并写出该不等式组的最大整式解.
并写出该不等式组的最大整式解.
解:解不等式x+1>0,得x>-1 …………………2分
解不等式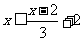 ,得
,得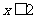 …………………2分
…………………2分
∴不等式组的解集为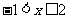 …………………1分
…………………1分
∴该不等式组的最大整数解是2 …………………1分
15. 解答下列各题:
(1)计算: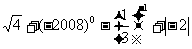 .
.
解:原式=2+1-3+2 …………………4分
=2 …………………2分
(2)化简: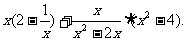
解:原式=2x-1+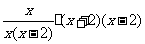 …………………4分
…………………4分
=2x-1+x+2
=3x+1 …………………2分
25. 如图,已知A、B、C是⊙O上的三个点,且AB=15cm,AC=3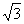 cm,∠BOC=60°.如果D是线段BC上的点,且点D到直线AC的距离为2,那么BD=
cm.
cm,∠BOC=60°.如果D是线段BC上的点,且点D到直线AC的距离为2,那么BD=
cm.

[参考答案]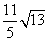
[解析]本题考查学生求解线段的长度,综合了圆的知识、解直角三角形的知识以及相似形的知识,其中运用了如何构造直角三角形的思想。由于∠COB=60º,∠A=30º,过点B作BH⊥AC于H,设D是BC上一点,DE⊥AC于点E,则DE=2,在直角三角形ABH中,AB=15,则AH=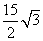 ,BH=
,BH=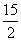 ,CH=AH-AC=
,CH=AH-AC=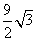 ,在直角三角形BCH中,由勾股定理可得:BH=
,在直角三角形BCH中,由勾股定理可得:BH=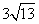 ,再由△CDE∽△CBH,得
,再由△CDE∽△CBH,得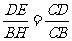 ,算得CD=
,算得CD=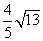 ,所以BD=
,所以BD=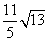
评分标准
A卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com