
4、⊙O1与⊙O2的半径分别为4cm和5cm,若O1O2=10cm,则两圆的位置关系是[ ]
A、外离 B、外切 C、相交 D、内切
3、如图所示的几幅图中,可以旋转180°与自身重合的是……………………[ ]
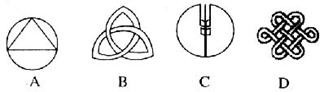
2、一元二次方程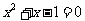 的根的情况是……………………………………[ ]
的根的情况是……………………………………[ ]
A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、无法判断
1、下列几何图形中,是中心对称图形而不是轴对称图形的是…………………[ ]
A、线段 B、平行四边形 C、矩形 D、圆
25.(本题12分)如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点.
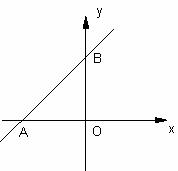 OA、OB的长度分别为a和b,且满足
OA、OB的长度分别为a和b,且满足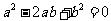 .
.
⑴判断△AOB的形状.
|
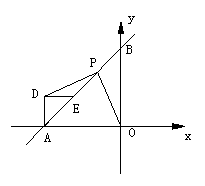
 ⑵如图②,正比例函数
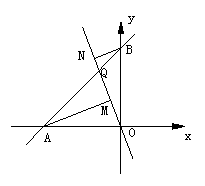
⑵如图②,正比例函数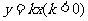 的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.
的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.
|
⑶如图③,E为AB上一动点,以AE为斜边作等腰直角△ADE,P为BE的中点,连结PD、PO,试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明.
|
24.(本题10分)如图①,△ABC≌△DEF,将△ABC和△DEF的顶点B与顶点E重合,把△DEF绕点B顺时针方向旋转,这时AC与DF相交于点O.
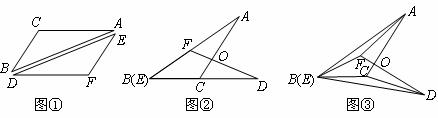
(1)当△DEF旋转至如图②位置,点B(E)、C、D在同一直线上时,∠AFD与∠DCA的数量关系是 .
(2)当△DEF继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO、AD,猜想BO与AD之间有怎样的位置关系?画出图形,写出结论,无需证明.
23.(本题9分)如图,在平面直角坐标系中,函数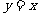 的图象
的图象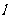 是第一、三象限的角平分线.
是第一、三象限的角平分线.
实验与探究:由图观察易知A(0,2)关于直线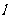 的对称点
的对称点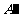 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线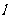 的对称点
的对称点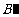 、
、 的位置,并写出它们的坐标:
的位置,并写出它们的坐标: 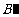 、
、 ;
;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线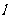 的对称点
的对称点 的坐标为
;
的坐标为
;
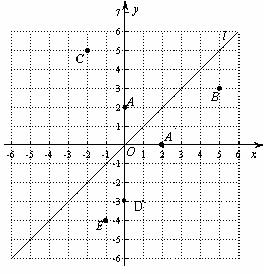 运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线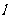 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
22.(本题8分)2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产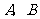 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产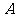 种购物袋
种购物袋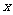 个,每天共获利
个,每天共获利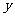 元.
元.
|
|
成本(元/个) |
售价(元/个) |
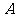 |
2 |
2.3 |
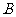 |
3 |
3.5 |
(1)求出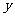 与
与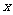 的函数关系式;
的函数关系式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?
21. (本题8分)如图,在平面直角坐标系中,点P
(本题8分)如图,在平面直角坐标系中,点P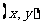 是第一象限直线
是第一象限直线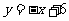 上的点,点A
上的点,点A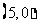 ,O是坐标原点,△PAO的面积为
,O是坐标原点,△PAO的面积为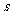 .
.
⑴求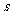 与
与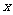 的函数关系式,并写出x的取值范围;
的函数关系式,并写出x的取值范围;
⑵探究:当P点运动到什么位置时△PAO的面积为10.
20.(本题7分)先化简,再求值: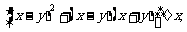 其中
其中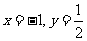 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com