4、方程 x ² = x 的解是­__________________

3、如图，要给这个长、宽、高分别为x、y、z的箱子打包，其打包方式如右图所示，则打包带的长至少要_________ (单位：mm)(用含x、y、z的代数式表示)

2、据有关资料显示，长江三峡工程电站的总装机容量是18200000千瓦，请你用科学记数法表示电站的总装机容量，应记为　　　　 千瓦　

1、已知点P(－2，3)，则点P关于x轴对称的点坐标是(　　 　　)

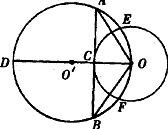
29、已知半径为R的⊙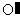经过半径为r的⊙O的圆心，⊙O与⊙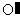交于E、F两点．　

(1)如图(1)，连结00'交⊙O于点C，并延长交⊙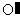于点D，过点C作⊙O的切线交⊙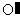于A、B两点，求OA·OB的值；　　

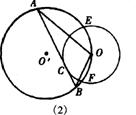
(2)若点C为⊙O上一动点，①当点C运动到⊙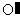时，如图(2)，过点C作⊙O的切线交⊙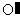，于A、B两点，则OA·OB的值与(1)中的结论相比较有无变化?请说明理由．

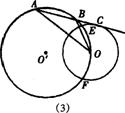
②当点C运动到⊙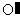外时，过点C作⊙O的切线，若能交⊙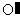于A、B两点，如图(3)，则OA·OB的值与(1)中的结论相比较有无变化?请说明理由．

28、如图：把一个等腰直角三角形ABC沿斜边上的高线CD(裁剪线)剪一刀，从这个三角形中剪下一部分，与剩下部分能拼成一个平行四边形ABCD(见示意图a)注意：以下探究过程中有画图要求的，工具不限，不必写画法和证明。

探究一：(1)想一想：判断四边形ABCD是平行四边形的依据是　　　　 。

(2)做一做：按上述的裁剪方法，请你拼一个与图a位置或形状不同的平行四边形，并在图b中画出示意图。

探究二：在等腰直角三角形ABC中，请你找出其它的裁剪线，把分割成的两部分拼出不同类型的特殊四边形。

(1)试一试：你能拼得所有不同类型的特殊四边形有　　　 ，它们的裁剪线分别是　　　　　 。

(2)画一画：请在图c中画出一个你拼得的特殊四边形示意图。

　 (a)　　　　　　　　　 (b)　　　　　　　　 (c)

26、已知：如图，AB是⊙O的一条弦，点C为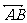的中点，CD是⊙O的直径，过C点的直线交AB所在直线于点E，交⊙O于点F。

(1)判定图中与的数量关系，并写出结论；

(2)将直线绕C点旋转(与CD不重合)，在旋转过程中，E点、F点的位置也随之变化，请你在下面两个备用图中分别画出在不同位置时，使(1)的结论仍然成立的图形，标上相应字母，选其中一个图形给予证明。

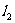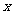25、如图，、分别表示一种白炽灯和一种节能灯的费用(费用=灯的售价+电费，单位：元)与照明时间(小时)的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样。

(1)根据图象分别求出、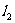的函数关系式；

(2)当照明时间为多少时，两种灯的费用相等？

(3)小亮房间计划照明2500小时，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法(直接给出答案，不必写出解答过程)。

24、在一块长16m，宽12m的矩形荒地上，要建造一个花园，要求花园所占面积为荒地面积的一半．下面分别是小明和小颖的设计方案．

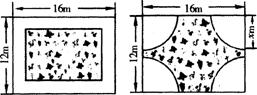
(1)你认为小明的结果对吗?请说明理由．

(2)请你帮助小颖求出图中的x(精确到0．1m)

(3)你还有其他的设计方案吗?请在图3中画出你所设计的草图，并加以说明．