
1、 的结果是( )(09常德)
的结果是( )(09常德)
A.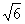 B.
B.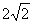 C.
C.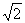 D.
D.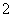
17.(2009,恩施)求代数式的值: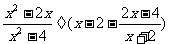 ,其中
,其中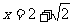
解: 原式=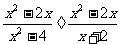
=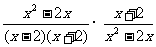
=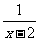
将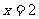 +
+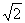 代入
代入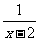 得:
得: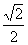
(2009,黄石)先化简,再求值
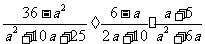 其中
其中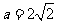 .
.
解:原式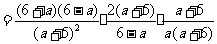
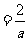 .
.
当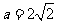 时,原式
时,原式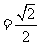 .
.
(2009,武汉)先化简,再求值: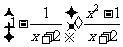 ,其中
,其中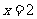 .
.
解:原式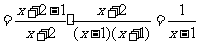
当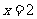 时,原式
时,原式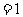 .
.
(2009,襄樊)分式方程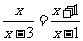 的解为( )D
的解为( )D
A.1 B.-1 C.-2 D.-3
(2009,襄樊)计算: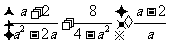
解:原式=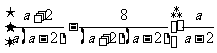
=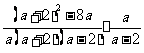
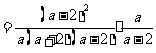
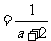
(2009,宜昌)当x=
时,分式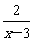 没有意义.3
没有意义.3
(2009,宜昌)化简: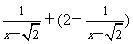
解: 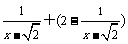
=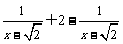
=2.
(2009,鄂州)使代数式 有意义的x的取值范围是( )D
有意义的x的取值范围是( )D
A、x>3 B、x≥3 C、 x>4 D 、x≥3且x≠4
(2009,荆门)已知x=2+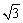 ,y=2-
,y=2-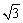 ,计算代数式
,计算代数式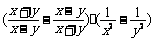 的值.
的值.
解: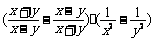 =
=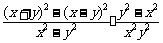
=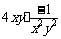 =
=
当x=2+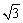 ,y=2-
,y=2-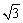 时,
时,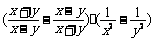 =-4
=-4
(2009,仙桃)分式方程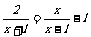 的解为________________.
的解为________________.
(2009,仙桃)先化简,再求值: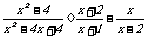 ,其中x=2-
,其中x=2-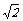 .
.
(2009,牡丹江)若关于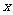 的分式方程
的分式方程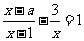 无解,则
无解,则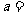 .1或-2
.1或-2
(2009,牡丹江)先化简: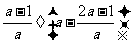 并任选一个你喜欢的数
并任选一个你喜欢的数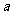 代入求值.
代入求值.
解:原式=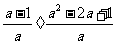
=
=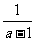
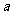 取0和1以外的任何数,计算正确都可给分
取0和1以外的任何数,计算正确都可给分
(2009,齐齐哈尔)先化简: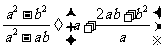 ,当
,当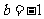 时,请你为
时,请你为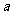 任选一个适当的数代入求值.
任选一个适当的数代入求值.
原式=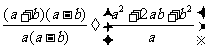
=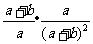
=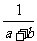
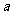 值正确
值正确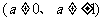 给1分,计算结果正确给分
给1分,计算结果正确给分
(2009,齐齐哈尔)某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金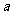 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同,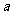 值应是多少?此时,哪种方案对公司更有利?
值应是多少?此时,哪种方案对公司更有利?
(1)解:设今年三月份甲种电脑每台售价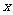 元
元

解得:
经检验: 是原方程的根,所以甲种电脑今年每台售价4000元.
是原方程的根,所以甲种电脑今年每台售价4000元.
(2)设购进甲种电脑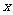 台,
台,
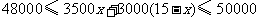
解得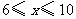
因为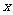 的正整数解为6,7,8,9,10,所以共有5种进货方案
的正整数解为6,7,8,9,10,所以共有5种进货方案
(3)设总获利为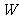 元,
元,
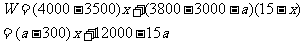
当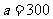 时,(2)中所有方案获利相同.
时,(2)中所有方案获利相同.
此时,购买甲种电脑6台,乙种电脑9台时对公司更有利
(2009,哈尔滨)先化简.再求代数式的值.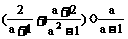 其中a=tan60°-2sin30°.
其中a=tan60°-2sin30°.
(2009,哈尔滨)跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来
(2009,河南)先化简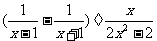 ,然后从
,然后从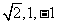 中选取一个你认为合适的数作为x的值代入求值.
中选取一个你认为合适的数作为x的值代入求值.
原式=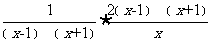
=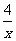 .
.
当x=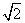 时,原式=
时,原式=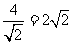 .
.
(2009,河北)已知a = 2,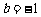 ,求
,求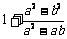 ÷
÷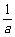 的值.
的值.
解:原式=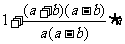
=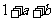 .
.
当a = 2,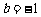 时,
时,
原式 = 2
(2009,安顺)已知分式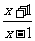 的值为0,那么
的值为0,那么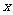 的值为______________。-1
的值为______________。-1
(2009,安顺)先化简,再求值: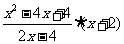 ,其中
,其中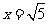

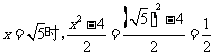
(2009,柳州)分式方程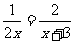 的解是( ) B
的解是( ) B
A.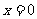 B.
B.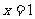 C.
C.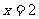 D.
D.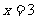
(2009,梧州)由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
解:(1)设甲队单独完成此项工程需x天,由题意得
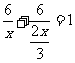
解之得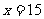
经检验,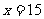 是原方程的解.
是原方程的解.
所以甲队单独完成此项工程需15天,
乙队单独完成此项工程需15×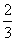 =10(天)
=10(天)
(2)甲队所得报酬: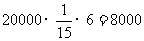 (元)
(元)
乙队所得报酬: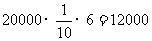 (元)
(元)
(2009,玉林)当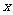 =
时,分式
=
时,分式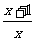 没有意义.0
没有意义.0
(2009,玉林)方程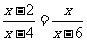 的解是( )
的解是( )
A.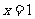 B.
B. 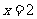 C.
C. 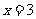 D.
D.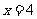
(2009,河池)铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70﹪)售完,那么超市在这两次苹果销售中共盈利多少元?
解:(1)设试销时这种苹果的进货价是每千克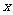 元,依题意,得)
元,依题意,得)
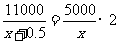
解之,得 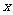
 5
5
经检验,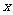
 5是原方程的解.
5是原方程的解.
(2)试销时进苹果的数量为: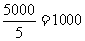 (千克)
(千克)
第二次进苹果的数量为:2×1000 2000(千克)
2000(千克)
盈利为: 2600×7+400×7×0.7-5000-11000 4160(元)
4160(元)
答:试销时苹果的进货价是每千克5元,商场在两次苹果销售中共盈利4160元.
(2009,贺州)解分式方程: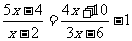
解:方程两边同乘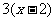 ,得
,得
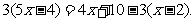
解这个方程,得 x=2
检验:当x=2时,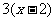 =0,所以x=2是增根,原方程无解
=0,所以x=2是增根,原方程无解
(2009,南宁)要使式子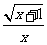 有意义,
有意义,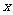 的取值范围是( )D
的取值范围是( )D
A.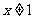 B.
B.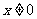 C.
C. D.
D.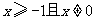
(2009,南宁)先化简,再求值:
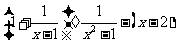 ,其中
,其中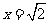
解: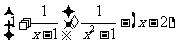
=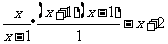
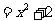
当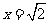 时,原式
时,原式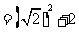
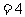
(2009,钦州)解方程: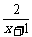 =1.
=1.
两边都乘以x+1,得
2=x+1. 7分
移项,合并同类项,得
x=1.
当x=1时, x+1=2≠0,
∴原方程的根是:x=1.
(2009,钦州)先化简,再求值: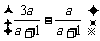 ·
· ,其中a=
,其中a=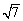 +1(精确到0
+1(精确到0 01).
01).
原式=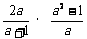
=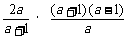
=2(a-1).
∵a=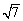 +1,
+1,
∴原式=2(a-1)
=2(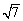 +1-1)
+1-1)
=2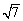 ≈5
≈5 29.
29.
(2009,白色)先化简,再求值: 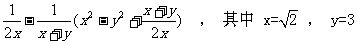
(2009,白色)在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成。
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元。若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
(2009,广州)解方程
解:两边乘以x(x-2),得
3(x-2)=2x
解得x=6
经检验,x=6是原方程的解。
(2009,梅州)先化简,再求值: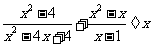 ,其中
,其中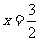 .
.
解:
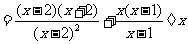
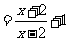
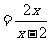
当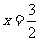 时,原式
时,原式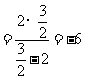
(2009,清远)当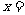 时,分式
时,分式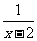 无意义.2
无意义.2
(2009,清远)解分式方程: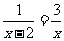
解:去分母,得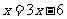
解得: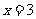
检验:把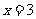 代入原方程得:左边=右边
代入原方程得:左边=右边
所以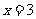 是原方程的解
是原方程的解
(2009,清远)化简: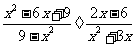
解:原式=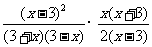
=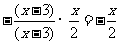
(2009,肇庆)若分式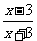 的值为零,则
的值为零,则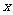 的值是( )A
的值是( )A
A.3
B. C.
C.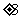 D.0
D.0
(2009,肇庆)观察下列各式: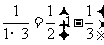 ,
,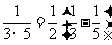 ,
,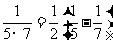 ,…,根据观察计算:
,…,根据观察计算: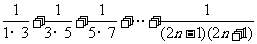 = .(n为正整数)
= .(n为正整数)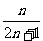
(2009,肇庆)已知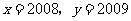 ,求代数式
,求代数式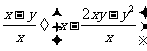 的值.
的值.
解: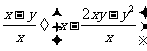
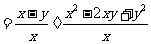
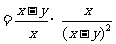
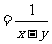
∵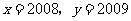 ,∴原式
,∴原式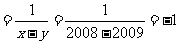
(2009,宁德)解分式方程: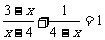 .
.
解:方程两边同乘以x-4,
3-x-1=x-4
解这个方程,得x=3
检验:当x==3时,x-4=-1≠0
∴ x=3是原方程的解
(2009,广东省)解方程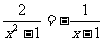 .
.
(2009,定西)计算: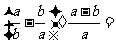 ( )A
( )A
A.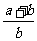 B.
B.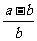 C.
C.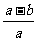 D.
D.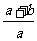
(2009,龙岩)计算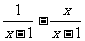 的结果为( )C
的结果为( )C
A.1 B.2 C.-1 D.-2
(2009,龙岩)方程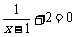 的解是
.6
的解是
.6
(2009,福州)若分式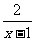 有意义,则x的取值范围是( )A
有意义,则x的取值范围是( )A
A.x≠1 B.x>1 C. x=1 D.x<1
(2009,定西)去年5月12日,四川省汶川县发生了里氏8.0级大地震,兰州某中学师生自愿捐款,已知第一天捐款4800元,第二天捐款6000元,第二天捐款人数比第一天捐款人数多50人,且两天人均捐款数相等,那么两天共参加捐款的人数是多少?人均捐款多少元?
解法1:设第一天捐款x人,则第二天捐款(x+50)人,
由题意列方程 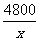 =
=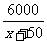 .
.
解得 x =200.
检验:当x =200时,x(x+50)≠0,
∴ x =200是原方程的解.
两天捐款人数x+(x+50)=450, 人均捐款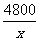 =24(元).
=24(元).
答:两天共参加捐款的有450人,人均捐款24元.
说明:只要求对两天捐款人数为450, 人均捐款为24元,不答不扣分.
解法2:设人均捐款x元,
由题意列方程 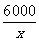 -
-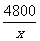 =50
.
=50
.
解得 x =24.
以下略.
(2009,福州)整理一批图书,如果由一个人单独做要花60小时。现先由一部分人用一小时整理,随后增加15人和他们一起又做了两小时,恰好完成整理工作。假设每个人的工作效率相同,那么先安排整理的人员有多少人?
解:设先安排整理的人员有x人,依题意得,
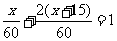
解得, x=10.
答:先安排整理的人员有10人.
(2009,泉州)计算: 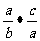 = .
= .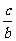
(2009,莆田)先化简。再求值:
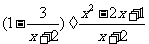 ,其中
,其中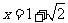 。
。
解:原式=
=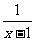
当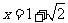 时,
时,
原式=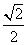 …
…
(2009,漳州)分式方程 的解是( )A
的解是( )A
A.1 B.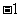 C.
C.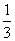 D.
D.
(2009,北京)解分式方程: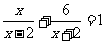 .
.
(2009,安徽)观察下列等式: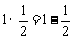 ,
,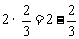 ,
,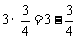 ,……
,……
(1)猜想并写出第n个等式;
[猜想]
(2)证明你写出的等式的正确性.
[证]
(1)猜想: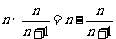
(2)证:右边=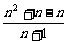 =
=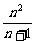 =左边,即
=左边,即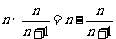
5.5 < x <8 .
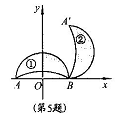 (2009,河南)如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转900得到月牙②,则点A的对应点A’的坐标为
[ ]B
(2009,河南)如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转900得到月牙②,则点A的对应点A’的坐标为
[ ]B
(A)(2,2) (B)(2,4)
(C)(4,2) (D)(1,2)
 (2009,牡丹江)
(2009,牡丹江)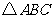 在如图所示的平面直角坐标系中,将
在如图所示的平面直角坐标系中,将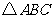 向右平移3个单位长度后得
向右平移3个单位长度后得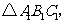 再将
再将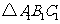 绕点
绕点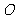 旋转
旋转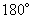 后得到
后得到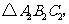 则下列说法正确的是( )D
则下列说法正确的是( )D
A.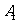 的坐标为
的坐标为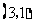 B.
B.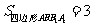
C.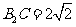 D.
D.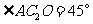
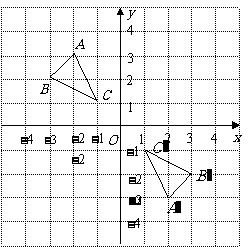
(2009,齐齐哈尔)如图,在平面直角坐标系中,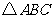 的顶点坐标为
的顶点坐标为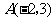 、
、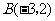 、
、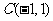 .
.
(1)若将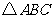 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的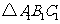 ;
;
(2)画出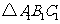 绕原点旋转
绕原点旋转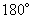 后得到的
后得到的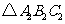 ;
;
(3) 与
与 是中心对称图形,请写出对称中心的坐标:___________;
是中心对称图形,请写出对称中心的坐标:___________;
(4)顺次连结 ,所得到的图形是轴对称图形吗?
,所得到的图形是轴对称图形吗?
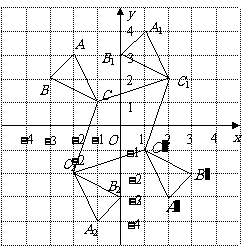 画出平移后的图形,
画出平移后的图形,
画出旋转后的图形
写出坐标(0,0),
答出“是轴对称图形”
(2009,哈尔滨)如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一
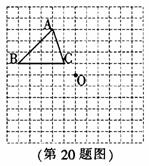 个△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.
个△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.
(1)在方格纸中,将△ABC向下平移5个单位长度得到△A1B1C1,
请画出△A1B1C1
(2)在方格纸中,将△ABC绕点O旋转180°得到△A2B2C2,
请画出△A2B2C2。
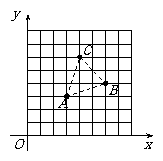
(2009,佳木斯)如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
(2009,武汉)如图,已知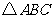 的三个顶点的坐标分别为
的三个顶点的坐标分别为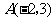 、
、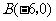 、
、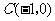 .
.
(1)请直接写出点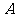 关于
关于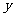 轴对称的点的坐标;
轴对称的点的坐标;
(2)将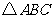 绕坐标原点
绕坐标原点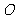 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点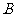 的对应点的坐标;
的对应点的坐标;
(3)请直接写出:以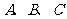 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点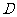 的坐标.
的坐标.
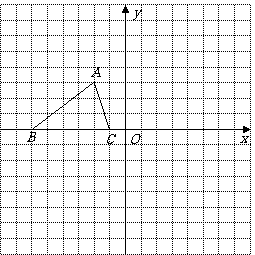
解:(1)(2,3);
(2)图形略.(0,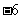 );
);
(3)(
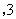 )或
)或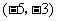 或
或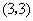 .
.
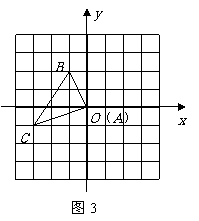
(2009,襄樊)如图3,在边长为1的正方形网格中,将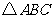 向右平移两个单位长度得到
向右平移两个单位长度得到 则与点
则与点 关于
关于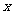 轴对称的点的坐标是( )D
轴对称的点的坐标是( )D
A.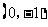 B.
B.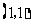 C.
C.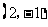 D.
D.
(2009,朝阳)在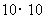 的网格纸上建立平面直角坐标系如图所示,在
的网格纸上建立平面直角坐标系如图所示,在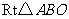 中,
中,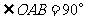 ,且点
,且点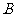 的坐标为
的坐标为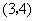 .
.
(1)画出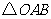 向左平移3个单位后的
向左平移3个单位后的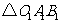 ,写出点
,写出点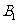 的坐标;
的坐标;

 (2)画出
(2)画出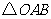 绕点
绕点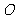 顺时针旋转
顺时针旋转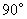 后的
后的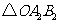 ,并求点
,并求点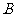 旋转到点
旋转到点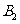 时,点
时,点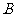 经过的路线长(结果保留
经过的路线长(结果保留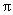 )
)
解:(1)画图)
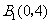
(2)画图
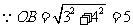
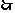 点
点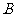 旋转到点
旋转到点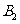 时,经过的路线长为
时,经过的路线长为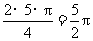
(2009,沈阳)如图,在平面直角坐标系中,已知点A(1,0)和点B(0,),点
C在坐标平面内.若以A、B、C为顶点构成的三角形是等腰
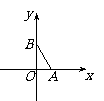 三角形,且底角为30º,则满足条件的点C有 个.
三角形,且底角为30º,则满足条件的点C有 个.
(2009,青岛)一艘轮船从港口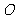 出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口
出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口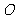 为坐标原点,正东方向为
为坐标原点,正东方向为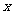 轴的正方向,正北方向为
轴的正方向,正北方向为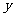 轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )A
轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )A
A.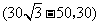 B.
B. C.
C.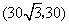 D.
D.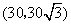
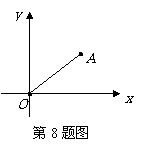
(2009,达州)在平面直角坐标系中,设点P到原点O的距离为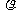 ,OP与x轴正方向的夹角为
,OP与x轴正方向的夹角为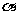 ,则用
,则用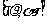 表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为
表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为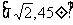 .若点Q的极坐标为
.若点Q的极坐标为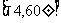 ,则点Q的坐标为 A
,则点Q的坐标为 A
A.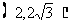 B.
B.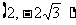 C.(2
C.(2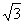 ,2) D.(2,2)
,2) D.(2,2)
(2009,乌鲁木奇)在平面直角坐标系中,点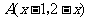 在第四象限,则实数
在第四象限,则实数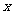 的取值范围是
.
的取值范围是
.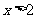
(2009,云南)在平面直角坐标系中,已知3个点的坐标分别为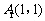 、
、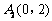 、
、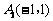 . 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以
. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以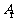 为对称中心的对称点
为对称中心的对称点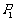 ,第2次电子蛙由
,第2次电子蛙由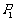 点跳到以
点跳到以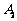 为对称中心的对称点
为对称中心的对称点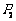 ,第3次电子蛙由
,第3次电子蛙由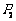 点跳到以
点跳到以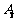 为对称中心的对称点
为对称中心的对称点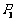 ,…,按此规律,电子蛙分别以
,…,按此规律,电子蛙分别以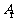 、
、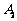 、
、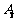 为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是
为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是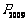 (_______ ,_______).
(_______ ,_______).
(−2,2)
(2009,嘉兴)如图,在直角坐标系中,已知点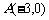 ,
,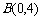 ,对△
,对△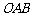 连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 ▲ .
连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 ▲ .
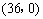
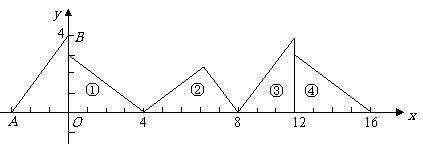
(2009,宁波)以方程组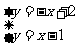 的解为坐标的点
的解为坐标的点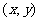 在平面直角坐标系中的位置是( )A
在平面直角坐标系中的位置是( )A
A.第一象限 B.第二象限 C.第三象限 D.第四象限
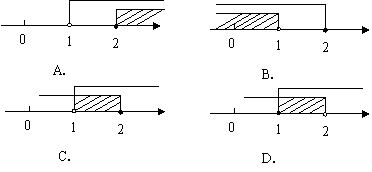
8.(2009,济南)不等式组 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
(2009,济南)自2008年爆发全球金融危机以来,部分企业受到了不同程度的影响,为落实“促民生、促经济”政策,济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年五月份的工资情况信息:
|
职工 |
甲 |
乙 |
|
月销售件数(件) |
200 |
180 |
|
月工资(元) |
1800 |
1700 |
(1)试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元?
(2)若职工丙今年六月份的工资不低于2000元,那么丙该月至少应销售多少件产品?
解:(1)设职工的月基本保障工资为 元,销售每件产品的奖励金额为
元,销售每件产品的奖励金额为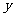 元
元
由题意得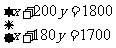
解这个方程组得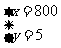
答:职工月基本保障工资为800元,销售每件产品的奖励金额5元.
(2)设该公司职工丙六月份生产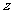 件产品
件产品
由题意得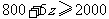
解这个不等式得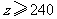
答:该公司职工丙六月至少生产240件产品
(2009,青岛)解不等式组: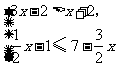
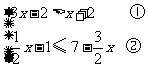
解:解不等式①得 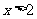 ,
,
解不等式②得 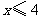 .
.
所以原不等式组的解集为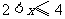 .
.
(2009,青岛)北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率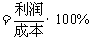 )
)
解:(1)设商场第一次购进 套运动服,由题意得:
套运动服,由题意得:
 ,
,
解这个方程,得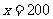 .
.
经检验,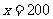 是所列方程的根.
是所列方程的根.
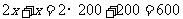 .
.
所以商场两次共购进这种运动服600套.
(2)设每套运动服的售价为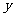 元,由题意得:
元,由题意得:
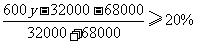 ,
,
解这个不等式,得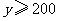 ,
,
所以每套运动服的售价至少是200元
(2009,威海)响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台.
(1)至少购进乙种电冰箱多少台?
(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
解:(1)设购买乙种电冰箱 台,则购买甲种电冰箱
台,则购买甲种电冰箱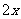 台,
台,
丙种电冰箱 台,根据题意,列不等式:
台,根据题意,列不等式:
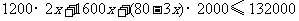 .
.
解这个不等式,得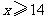 .
.
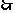 至少购进乙种电冰箱14台.
至少购进乙种电冰箱14台.
(2)根据题意,得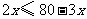 .
.
解这个不等式,得 .
.
由(1)知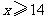 .
.
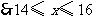 .
.
又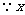 为正整数,
为正整数,
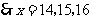 .··········································································································· 8分
.··········································································································· 8分
所以,有三种购买方案:
方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台;
方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台;
方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台.
(2009,烟台)如果不等式组 的解集是
的解集是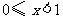 ,那么
,那么 的值为 .1
的值为 .1
(2009,淄博)解不等式:5x–12≤2(4x-3)
解:5x–12≤8x-6.
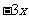 ≤6.
≤6.
x≥-2
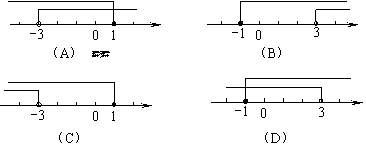
(2009,德州)不等式组 的解集在数轴上表示正确的是A
的解集在数轴上表示正确的是A
(2009,太原)某公司计划生产甲、乙两种产品共20件,其总产值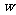 (万元)满足:1150<
(万元)满足:1150<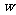 <1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
<1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
|
产品名称 |
每件产品的产值(万元) |
|
甲 |
45 |
|
乙 |
75 |
解:设计划生产甲产品 件,则生产乙产品
件,则生产乙产品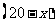 件,
件,
根据题意,得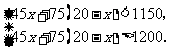
解得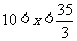 .
.
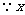 为整数,∴
为整数,∴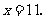 此时,
此时,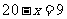 ( 件).
( 件).
答:公司应安排生产甲产品11件,乙产品9件.
 (2009,山西)不等式组
(2009,山西)不等式组 的解集在数轴上可表示为( )D
的解集在数轴上可表示为( )D
A. B.
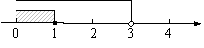
C. D.
(2008,,上海)不等式组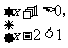 的解集是( C
)
的解集是( C
)
A. B.
B.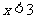 C.
C.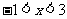 D.
D.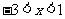
(2009,成都)解不等式组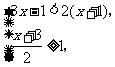 并在所给的数轴上表示出其解集。
并在所给的数轴上表示出其解集。
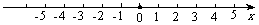
(2009,达州)解不等式组 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
解:由①解得 x>-31
由②解得 x≤12
∴不等式组的解集为-3<x≤13
(2009,凉山)若不等式组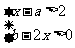 的解集是
的解集是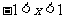 ,则
,则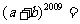 .1
.1
(2009,凉山)我国沪深股市交易中,如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股,若他期望获利不低于1000元,问他至少要等到该股票涨到每股多少元时才能卖出?(精确到0.01元)
解:设至少涨到每股 元时才能卖出.
元时才能卖出.
根据题意得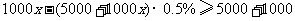
解这个不等式得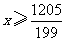 ,即
,即 .
.
答:至少涨到每股6.06元时才能卖出.
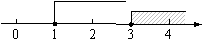
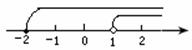 (2009,遂宁)把不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是
. .x>1
(2009,遂宁)把不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是
. .x>1
(2009,天津)解不等式组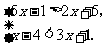
解:
由①得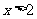 ,
,
由②得,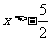
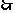 原不等式组的解集为
原不等式组的解集为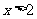
(2009,新疆)解不等式组: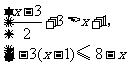 并在数轴上把解集表示出来.
并在数轴上把解集表示出来.
解:解不等式(1)得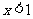
解不等式(2)得

所以不等式组的解集为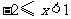 .
.
(2009,乌鲁木齐)某公司打算至多用1200元印制广告单.已知制版费50元,每印一张广告单还需支付0.3元的印刷费,则该公司可印制的广告单数量 (张)满足的不等式为
.
(张)满足的不等式为
.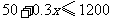
(2009,云南)不等式组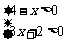 的解集是
.
的解集是
. 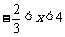
(2009,重庆)解不等式组: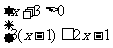
绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
|
类别 |
冰箱 |
彩电 |
|
进价(元/台) |
2 320 |
1 900 |
|
售价(元/台) |
2 420 |
1 980 |
(1) 按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买
了冰箱、彩电各一台,可以享受多少元的政府补贴?
(2)为满足农民需求,商场决定用不超过85 000元采购冰箱、彩电共40台, 且冰箱的数量不少于彩电数量的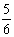 .
.
①请你帮助该商场设计相应的进货方案;
②哪种进货方案商场获得利润最大(利润=售价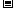 进价),最大利润是多少?
进价),最大利润是多少?
解:(1) (2 420+1 980)×13%=572
答: 可以享受政府572元的补贴.
(2) ①设冰箱采购x台,则彩电采购(40-x)台,根据题意,得
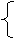 2 320x+1
900(40-x)≤85 000,
2 320x+1
900(40-x)≤85 000,
x≥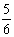 (40-x).
(40-x).
解不等式组,得 ≤x≤
≤x≤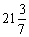
∵x为正整数.
∴x= 19,20,21.
∴该商场共有3种进货方案:
方案一:冰箱购买19台,彩电购买21台
方案二:冰箱购买20台,彩电购买20台;
方案三:冰箱购买21台,彩电购买19台.
②设商场获得总利润y元,根据题意,得
y=(2 420 - 2 320)x+(1 980 -1 900)(40-x)=20x+3 200
∵20>0, ∴y随x的增大而增大
∴当x=21时,y最大=20×21+3 200=3 620
答:方案三商场获得利润最大,最大利润是3 620元
(2009,杭州)在杭州市中学生篮球赛中,小方共打了10场球 .他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y比前5场比赛的平均得分x要高 .如果他所参加的10场比赛的平均得分超过18分
(1)用含x的代数式表示y;
(2)小方在前5场比赛中,总分可达到的最大值是多少?
(3)小方在第10场比赛中,得分可达到的最小值是多少?
(1)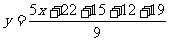 ;
;
(2)由题意有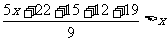 ,解得x<17,
,解得x<17,
所以小方在前5场比赛中总分的最大值应为17×5-1=84分;
(3)又由题意,小方在这10场比赛中得分至少为18×10 + 1=181分,
设他在第10场比赛中的得分为S,则有81+(22+15+12+19)+ S ≥181 .
解得S≥29,所以小方在第10场比赛中得分的最小值应为29分 .
(2009,湖州)随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1) 若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
(1)
设家庭轿车拥有量的年平均增长率为 ,则:
,则:
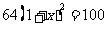 ,
,
解得: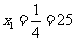 %,
%,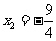 (不合题意,舍去),
(不合题意,舍去),
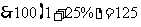 .
.
答:该小区到2009年底家庭轿车将达到125辆.
(2)
设该小区可建室内车位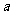 个,露天车位
个,露天车位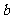 个,则:
个,则:

由①得: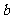 =150-5
=150-5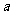 代入②得:
代入②得: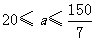 ,
,
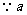 是正整数,
是正整数,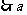 =20或21,
=20或21,
当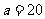 时
时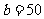 ,当
,当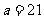 时
时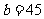 .
.
 方案一:建室内车位20个,露天车位50个;方案二:室内车位21个,露天车位45个.
方案一:建室内车位20个,露天车位50个;方案二:室内车位21个,露天车位45个.
(2009,宁波)不等式组 的解是 .
的解是 .
(2009,台州)解不等式组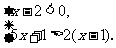
)解不等式①,得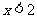 , ………………………………………………………3分
, ………………………………………………………3分
解不等式②,得 ,
,
∴不等式的解集为 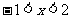 .
.
(2009,义乌)不等式组
 的解是
的解是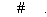
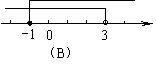
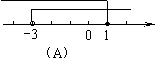
7.(2009,东营)不等式组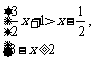 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是
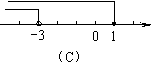
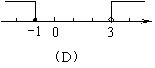
7.(2009,益阳)已知⊙O1和⊙O2的半径分别为1和4,如果两圆的位置关系为相交,那么圆心距O1O2的取值范围在数轴上表示正确的是 A
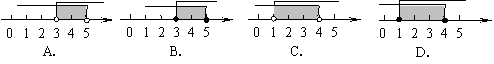
(2009,益阳)开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?请你一一写出.
解:(1)设每支钢笔x元,每本笔记本y元
依题意得: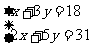
解得: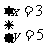
答:每支钢笔3元,每本笔记本5元
(2)设买a支钢笔,则买笔记本(48-a)本
依题意得: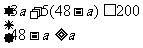
解得:
所以,一共有5种方案.
即购买钢笔、笔记本的数量分别为:
20,28; 21,27; 22,26; 23,25, 24,24
 (2009,邵阳)不等式组
(2009,邵阳)不等式组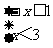 的解集在数轴上可以表示为 (C )
的解集在数轴上可以表示为 (C )
(2009,株洲)初中毕业了,孔明同学准备利用暑假卖报纸赚取140-200元钱,买一份礼物送给父母.已知:在暑假期间,如果卖出的报纸不超过1000份,则每卖出一份报纸可得0.1元;如果卖出的报纸超过1000份,则超过部分每份可得0.2元.
(1)请说明:孔明同学要达到目的,卖出报纸的份数必须超过1000份.
(2)孔明同学要通过卖报纸赚取140-200元,请计算他卖出报纸的份数在哪个范围内.
(1)如果孔明同学卖出1000份报纸,则可获得: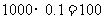 元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.)
元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.)
(2)设孔明同学暑假期间卖出报纸 份,由(1)可知
份,由(1)可知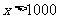 ,依题意得:
,依题意得:

解得 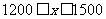
答:孔明同学暑假期间卖出报纸的份数在1200-1500份之间.
(2009,衡阳)解下列不等式组,并把解集在数轴上表示出来.
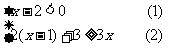
解:由(1)得:
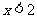
由(2)得:
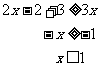
把它们的解集在数轴上表示如下:
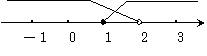

∴原不等式组的解集是 .
.
(2009,长春)不等式2x-6<0的解集是 B
(A)x>3.(B)x<3.(C)x>-3.(D)x<-3.
(2009,吉林)不等式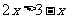 的解集为
.
的解集为
. >1
>1
(2009,江西)不等式组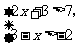 的解集是
.
的解集是
.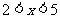
(2009,朝阳)某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节,感受冰雕艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车 辆,租车总费用为
辆,租车总费用为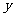 元.
元.
|
|
甲种客车 |
乙种客车 |
|
载客量(人/辆) |
45 |
30 |
|
租金(元/辆) |
280 |
200 |
(1)求出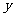 (元)与
(元)与 (辆)之间的函数关系式,指出自变量的取值范围;
(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?
(

(1)
(2)可以有结余,由题意知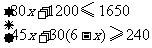
解不等式组得: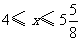
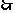 预支的租车费用可以有结余.
预支的租车费用可以有结余.
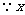 取整数
取整数 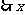 取4或5
取4或5
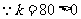
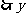 随
随 的增大而增大.
的增大而增大.
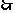 当
当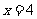 时,
时,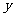 的值最小.
的值最小.
其最小值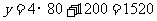 元
元
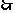 最多可结余1650
最多可结余1650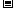 1520=130元
1520=130元
(2009,抚顺)某食品加工厂,准备研制加工两种口味的核桃巧克力,即原味核桃巧克力和益智核桃巧克力.现有主要原料可可粉410克,核桃粉520克.计划利用这两种主要原料,研制加工上述两种口味的巧克力共50块.加工一块原味核桃巧克力需可可粉13克,需核桃粉4克;加工一块益智核桃巧克力需可可粉5克,需核桃粉14克.加工一块原味核桃巧克力的成本是1.2元,加工一块益智核桃巧克力的成本是2元.设这次研制加工的原味核桃巧克力 块.
块.
(1)求该工厂加工这两种口味的巧克力有哪几种方案?
(2)设加工两种巧克力的总成本为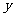 元,求
元,求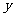 与
与 的函数关系式,并说明哪种加工方案使总成本最低?总成本最低是多少元?
的函数关系式,并说明哪种加工方案使总成本最低?总成本最低是多少元?
解:(1)根据题意,得

解得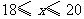
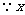 为整数
为整数
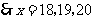
当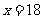 时,
时,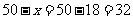
当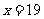 时,
时,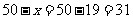
当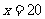 时,
时,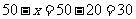
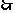 一共有三种方案:加工原味核桃巧克力18块,加工益智巧克力32块;加工原味核桃巧克力19块,加工益智巧克力31块,加工原味核桃巧克力20块,加工益智巧克力30块.6分
一共有三种方案:加工原味核桃巧克力18块,加工益智巧克力32块;加工原味核桃巧克力19块,加工益智巧克力31块,加工原味核桃巧克力20块,加工益智巧克力30块.6分
(2)
=
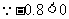
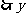 随
随 的增大而减小
的增大而减小
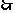 当
当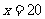 时,
时,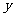 有最小值,
有最小值,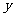 的最小值为84.
的最小值为84.
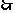 当加工原味核桃巧克力20块、加工益智巧克力30块时,总成本最低.总成本最低是84元.
当加工原味核桃巧克力20块、加工益智巧克力30块时,总成本最低.总成本最低是84元.
(2009,铁岭)为迎接国庆六十周年,某校团委组织了“歌唱祖国”有奖征文活动,并设立了一、二、三等奖.学校计划派人根据设奖情况买50件奖品,其中二等奖件数比一等奖件数的2倍还少10件,三等奖所花钱数不超过二等奖所花钱数的1.5倍.各种奖品的单价如下表所示.如果计划一等奖买 件,买50件奖品的总钱数是
件,买50件奖品的总钱数是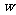 元.
元.
(1)求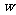 与
与 的函数关系式及自变量
的函数关系式及自变量 的取值范围;
的取值范围;
(2)请你计算一下,如果购买这三种奖品所花的总钱数最少?最少是多少元?
解:(1)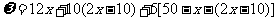
 .
.
由
得
∴自变量的取值范围是 ,且
,且 为整数.
为整数.
(2)∵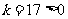 ,∴
,∴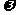 随
随 的增大而增大,当
的增大而增大,当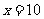 时,有
时,有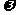 最小值.
最小值.
最小值为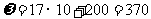 .
.
答:一等奖买10件,二等奖买10件,三等奖买30件时,所花的钱数最少,
最少钱数是370元
(2009,沈阳)不等式4x-2≤2的解集是 .
(2009,包头)不等式组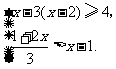 的解集是
.
的解集是
.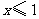
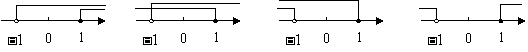 (2009,宁夏)把不等式组
(2009,宁夏)把不等式组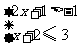 的解集表示在数轴上,下列选项正确的是( B )
的解集表示在数轴上,下列选项正确的是( B )
A. B. C. D.
(2009,青海)不等式组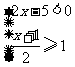 所有整数解的和是
.
所有整数解的和是
.
(2009,安顺)解不等式组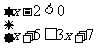 ;并写出它的整数解。
;并写出它的整数解。
解:解①得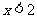 (3′)
解②得
(3′)
解②得
∴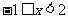 (7′) ∴所求不等式组的整数解为:-1. 0.
1 .
(7′) ∴所求不等式组的整数解为:-1. 0.
1 .
2.(2009,河南)不等式﹣2x<4的解集是 [ A ]
(A)x>﹣2 (B)x<﹣2 (C) x>2 (D) x<2
某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共l5台.三种家电的进价和售价如下表所示:

(1)在不超出现有资金的前提下,若购进电视机的数量和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定:农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下.
如果这15台家电全部销售给农民,国家财政最多需补贴农民多少元?
设购进电视机、冰箱各x台,则洗衣机为(15-2x)台
 15-2x≤
15-2x≤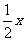 ,
,
依题意得:
2000x+2400x+1600(15-2x)≤32400
解这个不等式组,得6≤x≤7
∵x为正整数,∴x=6或7
方案1:购进电视机和冰箱各6台,洗衣机3台;
方案2:购进电视机和冰箱各7台,洗衣机1台
(2)方案1需补贴:(6×2100+6×2500+1×1700)×13%=4251(元);
方案2需补贴:(7×2100+7×2500+1×1700)×13%=4407(元);
∴国家的财政收入最多需补贴农民4407元.
(2009,牡丹江)某冰箱厂为响应国家“家电下乡”号召,计划生产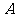 、
、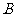 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
|
型号 |
A型 |
B型 |
|
成本(元/台) |
2200 |
2600 |
|
售价(元/台) |
2800 |
3000 |
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
解:(1)设生产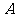 型冰箱
型冰箱 台,则
台,则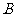 型冰箱为
型冰箱为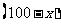 台,由题意得:
台,由题意得:
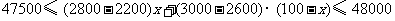
解得: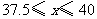
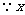 是正整数
是正整数
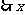 取38,39或40.
取38,39或40.
有以下三种生产方案:
|
|
方案一 |
方案二 |
方案三 |
|
A型/台 |
38 |
39 |
40 |
|
B型/台 |
62 |
61 |
60 |
(2)设投入成本为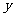 元,由题意有:
元,由题意有:
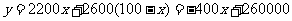
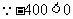
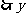 随
随 的增大而减小
的增大而减小
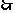 当
当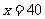 时,
时,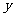 有最小值.
有最小值.
即生产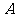 型冰箱40台,
型冰箱40台,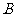 型冰箱50台,该厂投入成本最少
型冰箱50台,该厂投入成本最少
此时,政府需补贴给农民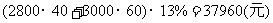
(3)实验设备的买法共有10种.
(2009,齐齐哈尔)一宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团20人准备同时租用这三种客房共7间,如果每个房间都住满,租房方案有( )C
A.4种 B.3种 C.2种 D.1种
(2009,齐齐哈尔)某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金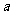 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同,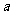 值应是多少?此时,哪种方案对公司更有利?
值应是多少?此时,哪种方案对公司更有利?
(1)解:设今年三月份甲种电脑每台售价 元
元
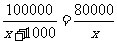
解得: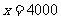
经检验: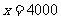 是原方程的根,
是原方程的根,
所以甲种电脑今年每台售价4000元.
(2)设购进甲种电脑 台,
台,
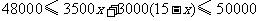
解得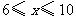
因为 的正整数解为6,7,8,9,10,所以共有5种进货方案
的正整数解为6,7,8,9,10,所以共有5种进货方案
(3)设总获利为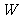 元,
元,
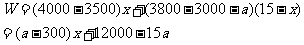
当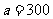 时,(2)中所有方案获利相同.
时,(2)中所有方案获利相同.
此时,购买甲种电脑6台,乙种电脑9台时对公司更有利.
(2009,哈尔滨)跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
(2009,黄冈)解不等式组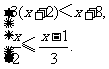
(2009,恩施)如果一元一次不等式组 的解集为
的解集为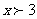 .则
.则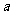 的取值范围是: C
的取值范围是: C
A.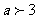 B.
B.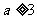 C.
C.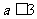 D.
D.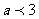
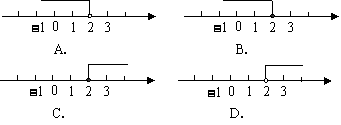
(2009,武汉)不等式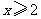 的解集在数轴上表示为( )C
的解集在数轴上表示为( )C
(2009,襄樊)为实现区域教育均衡发展,我市计划对某县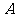 、
、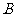 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所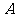 类学校和两所
类学校和两所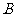 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所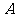 类学校和一所
类学校和一所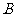 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所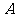 类学校和一所
类学校和一所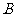 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的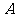 类学校不超过5所,则
类学校不超过5所,则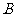 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县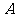 、
、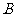 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到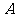 、
、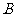 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
解:(1)设改造一所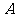 类学校和一所
类学校和一所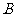 类学校所需的改造资金分别为
类学校所需的改造资金分别为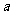 万元和
万元和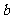 万元.依题意得:
万元.依题意得: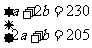
解之得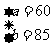
答:改造一所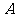 类学校和一所
类学校和一所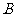 类学校所需的改造资金分别为60万元和85万元.
类学校所需的改造资金分别为60万元和85万元.
(2)设该县有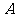 、
、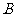 两类学校分别为
两类学校分别为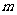 所和
所和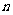 所.则
所.则
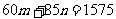
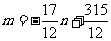
∵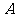 类学校不超过5所
类学校不超过5所
∴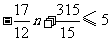
∴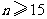
即: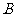 类学校至少有15所.
类学校至少有15所.
(3)设今年改造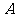 类学校
类学校 所,则改造
所,则改造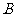 类学校为
类学校为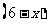 所,依题意得:
所,依题意得:

解之得
∵ 取整数
取整数
∴
即:共有4种方案.
(2009,鄂州)根据下图所示,对a、b、c三种物体的质量判断正确的是( )C
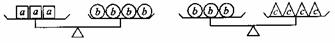
A、a<c B、a<b C、a>c D、b<c
(2009,荆门)若不等式组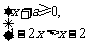 有解,则a的取值范围是( )A
有解,则a的取值范围是( )A
(A)a>-1. (B)a≥-1. (C)a≤1. (D)a<1.
(2009,荆门)星期天,小明和七名同学共8人去郊游,途中,他用20元钱去买饮料,商店只有可乐和奶茶,已知可乐2元一杯,奶茶3元一杯,如果20元钱刚好用完.
(1)有几种购买方式?每种方式可乐和奶茶各多少杯?
(2)每人至少一杯饮料且奶茶至少二杯时,有几种购买方式?
(1)设买可乐、奶茶分别为x、y杯,根据题意得
2x+3y=20(且x、y均为自然数)
∴x=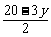 ≥0 解得y≤
≥0 解得y≤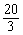
∴y=0,1,2,3,4,5,6.代入2x+3y=20 并检验得
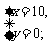

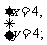
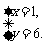
所以有四种购买方式,每种方式可乐和奶茶的杯数分别为:(亦可直接列举法求得)
10,0;7,2;4,4;1,6.
(2)根据题意:每人至少一杯饮料且奶茶至少二杯时,即y≥2且x+y≥8
由(1)可知,有二种购买方式.
(2009,咸宁)5月18日某地的最低气温是11℃,最高气温是27℃.下面用数轴表示这一天气温变化范围正确的是( )
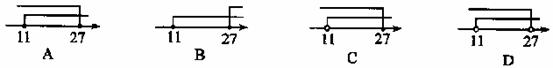
(2009,常德)解不等式组: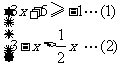
解不等式(1)得
解不等式(2)得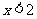
原不等式组的解集为
(2009,郴州)不等式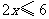 的解集为( )B
的解集为( )B
A.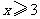 B.
B. 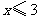 C.
C. 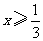 D.
D. 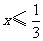
(2009,邵阳)不等式组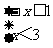 的解集在数轴上可以表示为 ( )
的解集在数轴上可以表示为 ( )

(2009,长沙)已知关于 的不等式组
的不等式组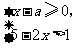 只有四个整数解,则实数
只有四个整数解,则实数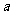 的取值范围是 .
的取值范围是 .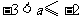
(2009,怀化)不等式组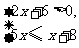 的解集在下列数轴上表示正确的是( )
的解集在下列数轴上表示正确的是( )
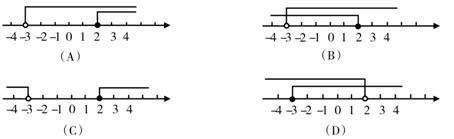
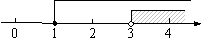
(2009,娄底)下列哪个不等式组的解集在数轴上表示如图2所示 ( )B
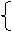 x≥2
x≥2
x<-1
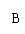
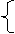 x≤2
x≤2
x>-1
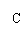
 x>2
x>2
x≤-1

 x<2
x<2
x≥-1
25.
 (本小题8分)(2009黄石)如图9,山顶建有一座铁塔,塔高CD=30m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距CD的水平距离AB。(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,
(本小题8分)(2009黄石)如图9,山顶建有一座铁塔,塔高CD=30m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距CD的水平距离AB。(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,
Sin23°≈0.391,cos23°≈0.921,tan23°≈0.424)
24.  (2009中山)如图所示,A、B两城市相距100km. 现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上. 已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.
请问:计划修筑的这条高速公路会不会穿越保护区. 为什么?(参考数据:
(2009中山)如图所示,A、B两城市相距100km. 现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上. 已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.
请问:计划修筑的这条高速公路会不会穿越保护区. 为什么?(参考数据: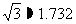 ,
,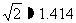 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com