21.　　 (本题满分l2分)

(2009宜宾)如图，在平面直角坐标系xoy中，等腰梯形OABC的下底边OA在x轴的正半轴上，BC∥OA，OC=AB．tan∠BA0=，点B的坐标为(7，4)．

(1)求点A、C的坐标；

(2)求经过点0、B、C的抛物线的解析式；

(3)在第一象限内(2)中的抛物线上是否存在一点P，使得经过点P且与等腰梯形一腰平行的直线将该梯形分成面积相等的两部分?若存在，请求出点P的横坐标；若不存在，请说明理由．

20.　　 (2009德州)某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风)，MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．

(1)当MN和AB之间的距离为0.5米时，求此时△EMN的面积；

(2)设MN与AB之间的距离为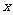米，试将△EMN的面积S(平方米)表示成关于x的函数；　

(3)请你探究△EMN的面积S(平方米)有无最大值，若有，请求出这个最大值；若没有，请说明理由．　

19.　　 (2009宁波)如图抛物线与x轴相交于点A、B，且过点C(5，4)．

(1)求a的值和该抛物线顶点P的坐标．

(2)请你设计一种平移的方法，使平移后抛物线的顶点落要第二象限，并写出平移后抛物线的解析式．

18.　　 (2009重庆)某电视机生产厂家去年销往农村的某品牌电视机每台的售价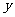(元)与月份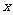之间满足函数关系，去年的月销售量(万台)与月份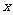之间成一次函数关系，其中两个月的销售情况如下表：

(1)求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？

(2)由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了，且每月的销售量都比去年12月份下降了。国家实施“家电下乡”政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴。受此政策的影响，今年3月份至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元，求的值(保留一位小数)

(参考数据：，，，)

17.　　 (2009义乌)如图，抛物线与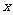轴的一个交点A在点(-2，0)和(-1，0)之间(包括这两点)，顶点C是矩形DEFG上(包括边界和内部)的一个动点，则

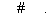
(填“”或“”)；

的取值范围是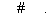

16.　　 (2009荆门)函数y=(x－2)(3－x)取得最大值时，x=______．

15.　　 (2009湖州)已知抛物线(＞0)的对称轴为直线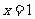，且经过点_，试比较和的大小：

　　　 _(填“>”，“<”或“=”)

14.　　 (2009南州)二次函数的图象关于原点O(0, 0)对称的图象的解析式是_________________。

13.　　 (2009黄石)已知二次函数y=ax²+bx+c(a≠0)的图象如图3所示，

下列结论：①abc＞0　 ②2a+b＜0　 ③4a－2b+c＜0　 ④a+c＞0，

其中正确结论的个数为(　　 )

A、4个　　　 B、3个　　　 C、2个　　　 D、1个

12.　　 (2009烟台)二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为(　　 )