
6.化简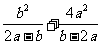 的结果是( )
的结果是( )
A.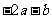 B.
B.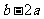 C.
C. D.
D.
5.计算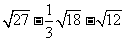 的结果是( )
的结果是( )
A.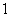 B.
B.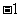 C.
C.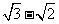 D.
D.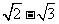
4.下列图形中,由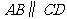 ,能得到
,能得到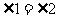 的是( )
的是( )
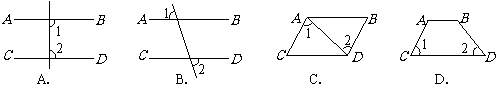
3.下列各式计算正确的是( )
A.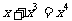 B.
B.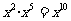
C.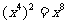 D.
D.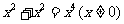
2.某种流感病毒的直径是0.00000008m,这个数据用科学记数法表示为( )
A.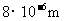 B.
B.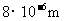
C.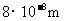 D.
D.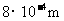
1. 的相反数是( )
的相反数是( )
A.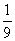 B.
B.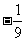 C.
C. D.
D.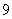
24.(本题满分10分)
解:(1)证明:在Rt△FCD中,
∵G为DF的中点,
∴ CG= FD.………………1分
同理,在Rt△DEF中,
EG= FD. ………………2分
∴ CG=EG.…………………3分
(2)(1)中结论仍然成立,即EG=CG.…………………………4分
证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.
在△DAG与△DCG中,
∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.
∴ AG=CG.………………………5分
在△DMG与△FNG中,
∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.
∴ MG=NG
在矩形AENM中,AM=EN. ……………6分
在Rt△AMG 与Rt△ENG中,
∵ AM=EN, MG=NG,
∴ △AMG≌△ENG.
∴ AG=EG.
∴ EG=CG. ……………………………8分
证法二:延长CG至M,使MG=CG,
连接MF,ME,EC, ……………………4分
在△DCG 与△FMG中,
∵FG=DG,∠MGF=∠CGD,MG=CG,
∴△DCG ≌△FMG.
∴MF=CD,∠FMG=∠DCG.
∴MF∥CD∥AB.………………………5分
∴ .
在Rt△MFE 与Rt△CBE中,
∵ MF=CB,EF=BE,
∴△MFE ≌△CBE.
∴ .…………………………………………………6分
∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°. …………7分
∴ △MEC为直角三角形.
∵ MG = CG,
∴ EG= MC.
∴ .………………………………8分
(3)(1)中的结论仍然成立,
即EG=CG.其他的结论还有:EG⊥CG.……10分
23.(本题满分10分)
解:(1)由题意,当MN和AB之间的距离为0.5米时,MN应位于DC下方,且此时△EMN中MN边上的高为0.5米.
所以,S△EMN= =0.5(平方米).
即△EMN的面积为0.5平方米. …………2分
(2)①如图1所示,当MN在矩形区域滑动,
即0<x≤1时,
△EMN的面积S= = ;……3分
②如图2所示,当MN在三角形区域滑动,
即1<x< 时,
如图,连接EG,交CD于点F,交MN于点H,
∵ E为AB中点,
∴ F为CD中点,GF⊥CD,且FG= .
又∵ MN∥CD,
∴ △MNG∽△DCG.
∴ ,即 .……4分
故△EMN的面积S=
= ; …………………5分
综合可得:
……………………………6分
(3)①当MN在矩形区域滑动时, ,所以有 ;………7分
②当MN在三角形区域滑动时,S= .
因而,当 (米)时,S得到最大值,
最大值S= = = (平方米). ……………9分
∵ ,
∴ S有最大值,最大值为 平方米. ……………………………10分
22.(本题满分10分)
解:延长BC交AD于E点,则CE⊥AD.……1分
在Rt△AEC中,AC=10,
由坡比为1: 可知:∠CAE=30°,………2分
∴ CE=AC·sin30°=10× =5,………3分
AE=AC·cos30°=10× = .……5分
在Rt△ABE中,
BE= = =11.……………………………8分
∵ BE=BC+CE,
∴ BC=BE-CE=11-5=6(米).
答:旗杆的高度为6米. …………………………………………10分
21.(本题满分9分)
解:(1)2007年销量为a万台,则a(1+40%)=350,a =250(万台).
…………………………………………………………………………3分
(2)设销售彩电x万台,则销售冰箱 x万台,销售手机(350- x)万台.由题意得:1500x+2000× +800(350 x)=500000. ……………6分
解得x=88. ………………………………………………………7分
∴ , .
所以,彩电、冰箱(含冰柜)、手机三大类产品分别销售88万台、132万台、130万部.………………………………………………………………8分
∴ 88×1500×13%=17160(万元),132×2000×13%=34320(万元),
130×800×13%=13520(万元).
获得的政府补贴分别是17160万元、34320万元、13520万元. ……9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com