
2.视力表对我们来说并不陌生.如图是视力表的一部分,
其中开口向上的两个“E”之间的变换是( )
A.平移 B.旋转 C.对称 D.位似
1.
 的相反数是( )
的相反数是( )
A. B.
B. C.
C. D.
D.
25.(本题满分12分)
如图①,某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成,在等腰梯形 中,
中, ,
, .对于抛物线部分,其顶点为
.对于抛物线部分,其顶点为 的中点
的中点 ,且过
,且过 两点,开口终端的连线
两点,开口终端的连线 平行且等于
平行且等于 .
.
(1)如图①所示,在以点 为原点,直线
为原点,直线 为
为 轴的坐标系内,点
轴的坐标系内,点 的坐标为
的坐标为 ,
,
试求 两点的坐标;
两点的坐标;
(2)求标志的高度(即标志的最高点到梯形下底所在直线的距离);
(3)现根据实际情况,需在标志截面图形的梯形部分的外围均匀镀上一层厚度为3cm的保护膜,如图②,请在图中补充完整镀膜部分的示意图,并求出镀膜的外围周长.

24.(本题满分10分)
某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价 元、每星期售出商品的利润为
元、每星期售出商品的利润为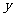 元,请写出
元,请写出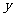 与
与 的函数关系式,并求出自变量
的函数关系式,并求出自变量 的取值范围;
的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
(3)请画出上述函数的大致图象.
23.(本题满分10分)
根据题意,解答下列问题:
(1)如图①,已知直线 与
与 轴、
轴、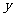 轴分别交于
轴分别交于 两点,求线段
两点,求线段 的长;
的长;
(2)如图②,类比(1)的求解过程,请你通过构造直角三角形的方法,求出两点 ,
, 之间的距离;
之间的距离;
(3)如图③, ,
, 是平面直角坐标系内的两点.
是平面直角坐标系内的两点.
求证: .
.

22.(本题满分8分)
观察下列方程及其解的特征:
(1) 的解为
的解为 ;
;
(2) 的解为
的解为 ;
;
(3) 的解为
的解为 ;
;
…… ……
解答下列问题:
(1)请猜想:方程 的解为 ;
的解为 ;
(2)请猜想:关于 的方程
的方程 的解为
的解为 ;
;
(3)下面以解方程 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.
解:原方程可化为 .
.
(下面请大家用配方法写出解此方程的详细过程)
21.(本题满分7分)
 如图,
如图, 为
为 的切线,A为切点.直线
的切线,A为切点.直线 与
与 交于
交于 两点,
两点, ,连接
,连接 .求证:
.求证: .
.
20.(本题满分6分)
为推进阳光体育活动的开展,某校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与,各活动小组人数分布情况的扇形图和条形图如下:


(1)求该班学生人数;
(2)请你补上条形图的空缺部分;
(3)求跳绳人数所占扇形圆心角的大小.
19.(本题满分5分)
计算: .
.
18.在平面直角坐标系中,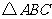 顶点
顶点 的坐标为
的坐标为 ,若以原点O为位似中心,画
,若以原点O为位似中心,画 的位似图形
的位似图形 ,使
,使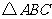 与
与 的相似比等于
的相似比等于 ,则点
,则点 的坐标为 .
的坐标为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com