
26.(本题14分)如图,已知直线 与直线
与直线 相交于点
相交于点 分别交
分别交 轴于
轴于 两点.矩形
两点.矩形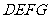 的顶点
的顶点 分别在直线
分别在直线 上,顶点
上,顶点 都在
都在 轴上,且点
轴上,且点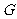 与点
与点 重合.
重合.
(1)求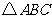 的面积;
的面积;
(2)求矩形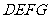 的边
的边 与
与 的长;
的长;
 (3)若矩形
(3)若矩形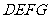 从原点出发,沿
从原点出发,沿 轴的反方向以每秒1个单位长度的速度平移,设移动时间为
轴的反方向以每秒1个单位长度的速度平移,设移动时间为 秒,矩形
秒,矩形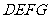 与
与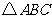 重叠部分的面积为
重叠部分的面积为 ,求
,求 关于
关于 的函数关系式,并写出相应的
的函数关系式,并写出相应的 的取值范围.
的取值范围.
 2009年山西省初中毕业学业考试试卷
2009年山西省初中毕业学业考试试卷
数 学
25.(本题12分)在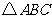 中,
中, 将
将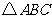 绕点
绕点 顺时针旋转角
顺时针旋转角


 得
得 交
交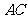 于点
于点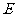 ,
, 分别交
分别交 于
于 两点.
两点.
 (1)如图1,观察并猜想,在旋转过程中,线段
(1)如图1,观察并猜想,在旋转过程中,线段 与
与 有怎样的数量关系?并证明你的结论;
有怎样的数量关系?并证明你的结论;
(2)如图2,当
 时,试判断四边形
时,试判断四边形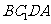 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的情况下,求 的长.
的长.
24.(本题8分)某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润 (万元)与进货量
(万元)与进货量 (吨)近似满足函数关系
(吨)近似满足函数关系 ;乙种水果的销售利润
;乙种水果的销售利润 (万元)与进货量
(万元)与进货量 (吨)近似满足函数关系
(吨)近似满足函数关系 (其中
(其中 为常数),且进货量
为常数),且进货量 为1吨时,销售利润
为1吨时,销售利润 为1.4万元;进货量
为1.4万元;进货量 为2吨时,销售利润
为2吨时,销售利润 为2.6万元.
为2.6万元.
(1)求 (万元)与
(万元)与 (吨)之间的函数关系式.
(吨)之间的函数关系式.
(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为 吨,请你写出这两种水果所获得的销售利润之和
吨,请你写出这两种水果所获得的销售利润之和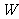 (万元)与
(万元)与 (吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
23. (本题8分)有一水库大坝的横截面是梯形
(本题8分)有一水库大坝的横截面是梯形 ,
, 为水库的水面,点
为水库的水面,点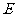 在
在 上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡
上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡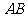 的长为12米,迎水坡上
的长为12米,迎水坡上 的长为2米,
的长为2米, 求水深.(精确到0.1米,
求水深.(精确到0.1米, )
)
22.(本题8分)某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
21.(本题8分)根据山西省统计信息网公布的数据,绘制了山西省2004~2008固定电话和移动电话年末用户条形统计图如下:

(1)填空:2004~2008移动电话年末用户的极差是 万户,固定电话年末用户的中位数是 万户;
(2)你还能从图中获取哪些信息?请写出两条.
20.(本题6分)已知每个网格中小正方形的边长都是1,图1
中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.
(1)填空:图1中阴影部分的面积是
(结果保留 );
);
(2)请你在图2中以图1为基本图案,借助轴对称、平移或旋转设计
一个完整的花边图案(要求至少含有两种图形变换).

19.(每小题4分,共12分)
(1)计算:
(2)化简:
(3)解方程:

18. 如图,在
如图,在 中,
中,


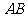 的垂
的垂
直平分线 交
交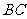 的延长线于点
的延长线于点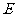 ,则
,则 的长为( )
的长为( )
A.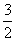 B.
B. C.
C. D.2
D.2
17.如图(1),把一个长为 、宽为
、宽为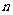 的长方形(
的长方形( )沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
A. B.
B. C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com