

29.(本小题满分12分)
 问题解决
问题解决
如图(1),将正方形纸片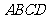 折叠,使点
折叠,使点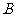 落在
落在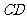 边上一点
边上一点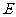 (不与点
(不与点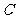 ,
,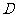 重合),压平后得到折痕
重合),压平后得到折痕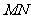 .当
.当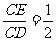 时,求
时,求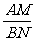 的值.
的值.

类比归纳
在图(1)中,若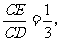 则
则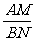 的值等于 ;若
的值等于 ;若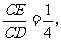 则
则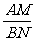 的值等于 ;若
的值等于 ;若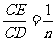 (
(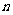 为整数),则
为整数),则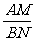 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)
联系拓广
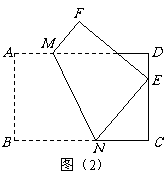 如图(2),将矩形纸片
如图(2),将矩形纸片 折叠,使点
折叠,使点 落在
落在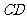 边上一点
边上一点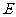 (不与点
(不与点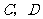 重合),压平后得到折痕
重合),压平后得到折痕 设
设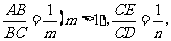 则
则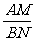 的值等于 .(用含
的值等于 .(用含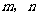 的式子表示)
的式子表示)
2009年山西省太原市初中毕业生学业考试试卷
28.(本小题满分9分)
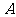 、
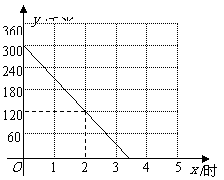
、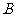 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往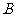 城,乙车驶往
城,乙车驶往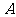 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距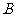 城高速公路入口处的距离
城高速公路入口处的距离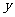 (千米)与行驶时间
(千米)与行驶时间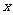 (时)之间的关系如图.
(时)之间的关系如图.
(1)求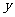 关于
关于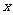 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为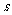 (千米).请直接写出
(千米).请直接写出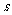 关于
关于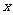 的表达式;
的表达式;
 (3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为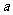 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度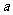 .在下图中画出乙车离开
.在下图中画出乙车离开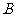 城高速公路入口处的距离
城高速公路入口处的距离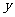 (千米)与行驶时间
(千米)与行驶时间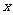 (时)之间的函数图象.
(时)之间的函数图象.
26.(本小题满分9分)
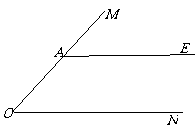
如图,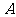 是
是 边
边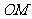 上一点,
上一点,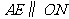 .
.
(1)在图中作 的角平分线
的角平分线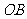 ,交
,交 于点
于点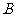 ;(要求:尺规作图,保留作图痕迹,不写作法和证明)
;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)在(1)中,过点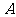 画
画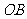 的垂线,垂足为点
的垂线,垂足为点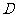 ,交
,交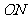 于点
于点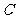 ,连接
,连接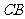 ,将图形补充完整,并证明四边形
,将图形补充完整,并证明四边形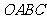 是菱形.
是菱形.
27(本小题满分8分)
某中学九年级有8个班,要从中选出两个班代表学校参加社区公益活动.各班都想参加,但由于特定原因,一班必须参加,另外从二至八班中再选一个班.有人提议用如下的方法:在同一个品牌的四个乒乓球上分别标上数字1,2,3,4,并放入一个不透明的袋中,摇匀后从中随机摸出两个乒乓球,两个球上的数字和是几就选几班,你认为这种方法公平吗?请用列表或画树状图的方法说明理由.
25.(本小题满分8分)
为了解某校学生每周购买瓶装饮料的情况,课外活动小组从全校30个班中采用科学的方法选了5个班.并随机对这5个班学生某一天购买瓶装饮料的瓶数进行了统计,结果如下图所示.
(1)求该天这5个班平均每班购买饮料的瓶数;
(2)估计该校所有班级每周(以5天计)购买饮料的瓶数;
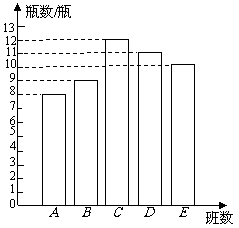 (3)若每瓶饮料售价在1.5元至2.5元之间,估计该校所有学生一周用于购买瓶装饮料的费用范围.
(3)若每瓶饮料售价在1.5元至2.5元之间,估计该校所有学生一周用于购买瓶装饮料的费用范围.
24.(本小题满分8分)
如图,从热气球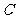 上测得两建筑物
上测得两建筑物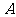 、
、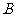 底部的俯角分别为30°和
底部的俯角分别为30°和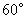 .如果这时气球的高度
.如果这时气球的高度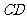 为90米.且点
为90米.且点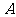 、
、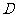 、
、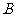 在同一直线上,求建筑物
在同一直线上,求建筑物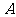 、
、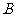 间的距离.
间的距离.
23.(本小题满分6分)
某公司计划生产甲、乙两种产品共20件,其总产值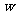 (万元)满足:1150<
(万元)满足:1150< <1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
<1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
|
产品名称 |
每件产品的产值(万元) |
|
甲 |
45 |
|
乙 |
75 |
22.(本小题满分5分)
已知,二次函数的表达式为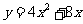 .写出这个函数图象的对称轴和顶点坐标,并求图象与
.写出这个函数图象的对称轴和顶点坐标,并求图象与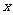 轴的交点的坐标.
轴的交点的坐标.
解答应写出文字说明、证明过程或演算步骤
21.(每小题满分5分)
化简: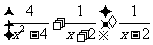
20.如图,在等腰梯形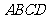 中,
中,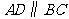 ,
,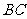 =4
=4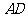 =
=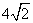 ,
,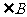 =45°.直角三角板含45°角的顶点
=45°.直角三角板含45°角的顶点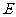 在边
在边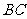 上移动,一直角边始终经过点
上移动,一直角边始终经过点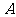 ,斜边与
,斜边与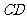 交于点
交于点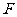 .若
.若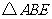 为等腰三角形,则
为等腰三角形,则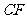 的长等于
.
的长等于
.
19.有两把不同的锁和三把钥匙,其中两把钥匙分别能打开其中一把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com