
5.满足2(x-1)≤x+2的正整数x有多少个( )
A.3 B.4 C.5 D.6
4.《广东省2009年重点建设项目计划(草案)》显示,港珠澳大桥工程估算总投资726亿元,用科学记数法表示正确的是( )
A.  元 B.
元 B. 元 C.
元 C.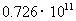 元 D.
元 D.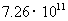 元
元
3.如图所示几何体的主(正)视图是( )
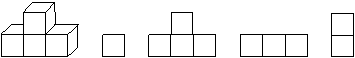
A. B. C. D.
2.计算 结果是( )
结果是( )
A.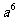 B.
B. C.
C.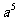 D.
D.
1.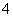 的算术平方根是( )
的算术平方根是( )
A. B.
B. C.
C. D.
D.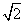
23.本题满分 11 分.
(提示:为了方便答题和评卷,建议在答题卡上画出你认为必须的图形)
如图 12,已知直线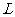 过点
过点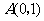 和
和 ,
,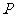 是
是 轴正半轴上的动点,
轴正半轴上的动点, 的垂直平分线交
的垂直平分线交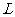 于点
于点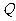 ,交
,交 轴于点
轴于点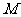 .
.
(1)直接写出直线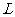 的解析式;
的解析式;
(2)设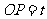 ,
,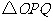 的面积为
的面积为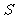 ,求
,求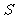 关于t的函数关系式;并求出当
关于t的函数关系式;并求出当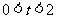 时,
时,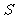 的最大值;
的最大值;
(3)直线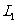 过点
过点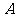 且与
且与 轴平行,问在
轴平行,问在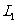 上是否存在点
上是否存在点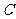 , 使得
, 使得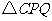 是以
是以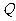 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.

22.本题满分 10 分.
如图 11,矩形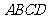 中,
中,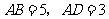 .点
.点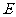 是
是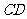 上的动点,以
上的动点,以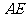 为直径的
为直径的 与
与 交于点
交于点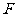 ,过点
,过点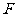 作
作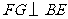 于点
于点 .
.
(1)当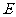 是
是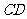 的中点时:
的中点时:
① 的值为______________;
的值为______________;
② 证明: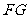 是
是 的切线;
的切线;
(2)试探究: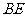 能否与
能否与 相切?若能,求出此时
相切?若能,求出此时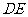 的长;若不能,请说明理由.
的长;若不能,请说明理由.


21.本题满分 8 分.
如图10,已知抛物线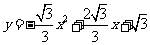 与
与 轴的两个交点为
轴的两个交点为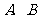 ,与y轴交于点
,与y轴交于点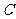 .
.
(1)求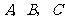 三点的坐标;
三点的坐标;
(2)求证: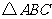 是直角三角形;
是直角三角形;
(3)若坐标平面内的点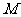 ,使得以点
,使得以点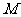 和三点
和三点 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点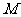 的坐标.(直接写出点的坐标,不必写求解过程)
的坐标.(直接写出点的坐标,不必写求解过程)

20.本题满分 8 分.
“五·一”假期,梅河公司组织部分员工到A、B、C三地旅游,公司购买前往各地的车票种类、数量绘制成条形统计图,如图9.根据统计图回答下列问题:
(1)前往 A地的车票有_____张,前往C地的车票占全部车票的________%;
(2)若公司决定采用随机抽取的方式把车票分配给 100 名员工,在看不到车票的条件下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去 B 地车票的概率为______;
(3)若最后剩下一张车票时,员工小张、小李都想要,决定采用抛掷一枚各面分别标有数字1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李.”试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
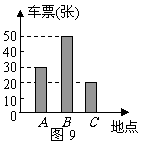
19.本题满分 8 分.
如图 8,梯形ABCD中,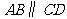 ,点
,点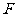 在
在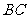 上,连
上,连 与
与 的延长线交于点G.
的延长线交于点G.
(1)求证: ;
;
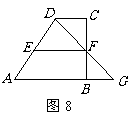 (2)当点F是BC的中点时,过F作
(2)当点F是BC的中点时,过F作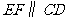 交
交 于点
于点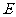 ,若
,若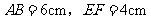 ,求
,求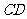 的长.
的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com