(四)基础性训练
1．
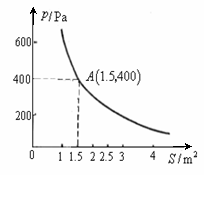某校科技小组进行野外考察，途中遇到一片的烂泥湿地．为了人员和设备安全迅速地通过这片湿地，他们沿着前进路线铺了若干块大小不同的木板，构筑成一条临时通道．下图是小明通过临时通道时踩在大小不同的木板上对烂泥湿地的压强的图象．已知当压力不变时，木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数.
(1)请直接写出p与S之间的关系式和自变量取值范围；
(2)当木板面积为0.2 m2时，压强是多少？
2．某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．
设每个房间每天的定价增加x元．求：
(1)房间每天的入住量y(间)关于x(元)的函数关系式．
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式．
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式；当每个房间的定价为每天多少元时，w有最大值？最大值是多少？
(三)数学化认识
|
教学环节 |
想一想 |
|||||||||||||
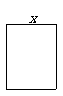 (一)问题导入如图，是一块长方形的镜面玻璃，玻璃的宽是x m． (1)若镜面玻璃的长是y m，面积为1m2，求y与x之间的函数关系式，并画出该函数图象的草图； (2)若镜面玻璃的长与宽的比是2∶1，其周长是l m，求l与x之间的函数关系式，并画出该函数图象的草图； (3)若镜面玻璃的长与宽的比是2∶1，其面积是s m2，求s与x之间的函数关系式，并画出该函数图象的草图； (注意：请把图象画在下面的直角坐标系中)  (二)建构活动 问题1 现有一块长方形的镜面玻璃，玻璃的宽是x m．在它的四周镶上与它的周长相等的边框，制成一面镜子．镜子的长与宽的比是2∶1，已知边框的价格是每米10元． (1)若制作边框的费用为y元，求y与x之间的函数关系式； (2)若镜面玻璃的价格是每平方米50元，另外制作这面镜子还需加工费10元． ①求制作这面镜子的总费用w(单位：元)与x之间的函数关系式； ②如果制作这面镜子共花了17元，求这面镜子的长和宽． 问题2 随着销量的增加，制造厂制作镜面玻璃的某种原料的需求量也在增加，其每天的需求量y(千克)与生产时间x(天)之间的关系如折线图所示.这些原料在第30天后每天的需求量比前一天增加100千克. (1)分别求出x≤30和x≥30时y与x之间的关系式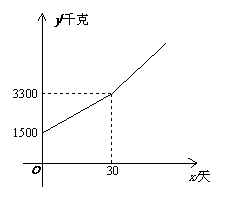；  (2)如果这些原料每天的需求量大于或等于4000千克时需要进行加班生产，那么应从第几天开始进行加班生产？问题3 该厂生产了一种成本为20元∕个的小镜子投放市场进行试销．经过调查，得到如下数据：
(1)认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y(个)与x(元∕个)之间的关系式； (2)当销售单价定为多少时，该厂试销这种镜子每天获得的总利润最大？最大利润是多少？(总利润=每个镜子的利润×销售量) (3)当地物价部门规定，这种镜子的销售单价最高不能超过45元/个，那么销售单价定为多少时，该厂试销这种镜子每天获得的利润最大？ 用函数解决实际问题时的主要方法、策略和注意事项是本节课的重点，在生活实际中建立函数的模型解决问题是本节课的难点。 3．进一步体会函数的思想和数形结合的思想。 2．在解决实际问题的过程中，关注三种函数之间的区别和联系，完善对函数的认识； 1．经历运用三种函数(反比例函数、一次函数和二次函数)解决实际问题的过程，总结三种函数在解决实际问题时的主要方法和策略，熟练核心技能； 28．(本题满分10分)
令x=0得y=2． ∴B(0，2) ············································· 1分 ∵ ∴A(-2，3)··········································· 3分 (2)当点P是 AB的延长线与x轴交点时，
当点P在x轴上又异于AB的延长线与x轴的交点时， 在点P、A、B构成的三角形中， 综合上述： (3)作直线AB交x轴于点P，由(2)可知：当PA-PB最大时，点P是所求的点 ····· 8分 作AH⊥OP于H． ∵BO⊥OP， ∴△BOP∽△AHP ∴ 由(1)可知：AH=3、OH=2、OB=2， ∴OP=4，故P(4，0) ···················································································· 10分 注：求出AB所在直线解析式后再求其与x轴交点P(4，0)等各种方法只要正确也相应给分． 27． 证明：(1)∵∠A=30°，∠ACB=90°，D是AB的中点． ∴BC=BD， ∠B=60° ∴△BCD是等边三角形．······································ 1分 又∵CN⊥DB， ∴ ∵∠EDF=90°，△BCD是等边三角形． ∴∠ADG=30°，而∠A=30°． ∴GA=GD． ∵GM⊥AB
又∵AD=DB ∴AM=DN ··················································· 4分 (2)∵DF∥AC ∴∠1=∠A=30°，∠AGD=∠GDH=90°， ∴∠ADG=60°． ∵∠B=60°，AD=DB， ∴△ADG≌△DBH ∴AG=DH，····················································· 6分 又∵∠1=∠A，GM⊥AB，HN⊥AB， ∴△AMG≌△DNH． ∴AM=DN ． ·············································· 8分 26．(本题满分7分) 解：(1) 所以一个书包的价格是30元． ··············································································· 2分 (注：用其它方法解出正确答案也给予相应的分值) (2)设还能为x 名学生每人购买一个书包和一件文化衫，根据题意得：···················· 3分
…… 解之得： 所以不等式组的解集为： ∵x为正整数， ∴x=30 ················································································································ 6分 答：剩余经费还能为30名学生每人购买一个书包和一件文化衫．···························· 7分 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
解：(1)抛物线
与y轴的交于点B，
．············································· 5分
．
················································································ 7分
····································································································· 9分
(本题满分8分)
····················································· 2分
∴
················································· 3分
(元) ······································································· 1分
4分
·························································· 5分