
7. P1(x1,y1),P2(x2,y2)是正比例函数y= -x图象上的两点,则下列判断正确的是
A.y1>y2 B.y1<y2
C.当x1<x2时,y1>y2 D.当x1<x2时,y1<y2
6. 据统计,2008年在国际金融危机的强烈冲击下,我国国内生产总值约
30 067 000 000 000元,仍比上年增长9.0%.30 067 000 000 000元用科学记数法表示为
A.30 067×109元 B.300.67×1011元
C.3.006 7×1013元 D.0.300 67×1014元
5. 为测量如图所示上山坡道的倾斜度,小明测得图中所示
 的数据(单位:米),则该坡道倾斜角α的正切值是
的数据(单位:米),则该坡道倾斜角α的正切值是
A.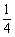 B.4
B.4
C.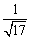 D.
D.
4. 二次函数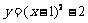 的图象上最低点的坐标是
的图象上最低点的坐标是
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
3. 从红桃A、黑桃A、梅花A、方块A四张牌中,随机抽取一张,则抽到方块A的概率为
从红桃A、黑桃A、梅花A、方块A四张牌中,随机抽取一张,则抽到方块A的概率为
A.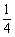 B.
B. C.
C.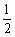 D.1
D.1
2. 外切两圆的圆心距是7,其中一圆的半径是4,则另一圆的半径是
A.11 B.7 C.4 D.3
1. 计算:-2+3 =
A.5 B.-5 C.1 D.-1
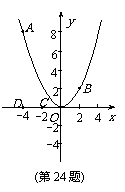
24. (本题12分)如图,已知点A(-4,8)和点B(2,n)在抛物线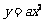 上.
上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线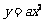 ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
浙江省2009年初中毕业生学业考试(舟山卷)
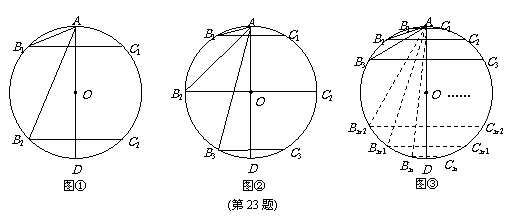
23.(本题10分)如图,AD是⊙O的直径.
(1) 如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2) 如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,
∠B3的度数;
(3) 如图③,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,请你用含n的代数式表示∠Bn的度数(只需直接写出答案).
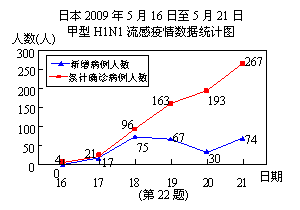
22.(本题10分)2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1) 在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
 (2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3) 甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com