
3.下列运算正确的是( ▲ )
A.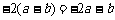 B.
B.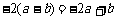
C.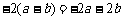 D.
D.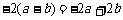
2.若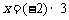 ,则x的倒数是( ▲ )
,则x的倒数是( ▲ )
A.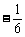 B.
B.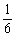 C.
C.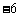 D.6
D.6
1.实数x,y在数轴上的位置如图所示,则( ▲ )
 A.
A.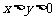 B.
B.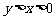
C.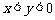 D.
D.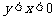
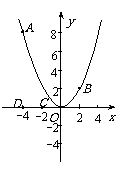
24. (本题14分)如图,已知点A(-4,8)和点B(2,n)在抛物线
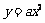 上.
上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线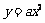 ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
浙江省2009年初中毕业生学业考试(衢州卷)
23.(本题12分)如图,AD是⊙O的直径.
 (1) 如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(1) 如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2) 如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,
∠B3的度数;
(3) 如图③,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,请你用含n的代数式表示∠Bn的度数(只需直接写出答案).

22.(本题12分)2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
 (1) 在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
(1) 在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
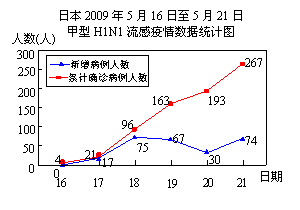 (2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3) 甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
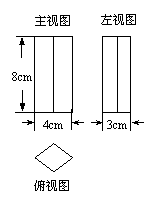
21.(本题10分)一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.

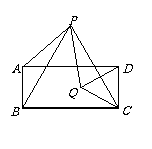
20.(本题8分)如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.
 求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
19.(本题8分)水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:

|
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
第8天 |
|
售价x(元/千克) |
400 |
|
250 |
240 |
200 |
150 |
125 |
120 |
|
销售量y(千克) |
30 |
40 |
48 |
|
60 |
80 |
96 |
100 |
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1) 写出这个反比例函数的解析式,并补全表格;
(2) 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
18.(本题8分)解不等式组 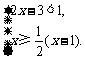

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com