25．(本题满分12分)

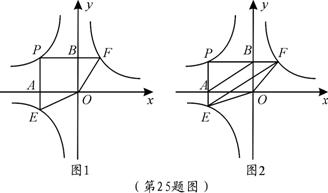
如图，点P是双曲线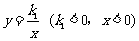上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交双曲线y= 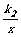(0＜k₂＜|k₁|)于E、F两点．

(1)图1中，四边形PEOF的面积S₁=　　 ▲　　 (用含k₁、k₂的式子表示)；(3分)

(2)图2中，设P点坐标为(－4，3)．

①判断EF与AB的位置关系，并证明你的结论；(4分)

②记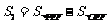，S₂是否有最小值？若有，求出其最小值；若没有，请说明理由．(5分)

24．(本题满分10分)

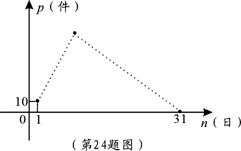
5月份，某品牌衬衣正式上市销售．5月1日的销售量为10件，5月2日的销售量为35件，以后每天的销售量比前一天多25件，直到日销售量达到最大后，销售量开始逐日下降，至此，每天的销售量比前一天少15件，直到5月31日销售量为0．设该品牌衬衣的日销量为p(件)，销售日期为n(日)，p与n之间的关系如图所示．

(1)写出p关于n的函数关系式p = 　　　▲　　　 (注明n的取值范围)；(3分)

(2)经研究表明，该品牌衬衣的日销量超过

150件的时间为该品牌衬衣的流行期．请问：该品牌衬衣本月在市面的流行期是多少天？(4分)

(3)该品牌衬衣本月共销售了　 ▲　 件．(3分)

23．(本题满分10分)

已知抛物线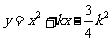(k为常数，且k＞0)．

(1)证明：此抛物线与x轴总有两个交点；(4分)

(2)设抛物线与x轴交于M、N两点，若这两点到原点的距离分别为OM、ON，且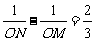，求k的值．(6分)

22．(本题满分10分)

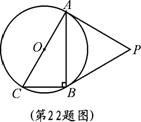如图，⊙O是Rt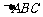的外接圆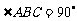，，点P是圆外一点，PA切⊙O于点A，且PA = PB．

(1)求证：PB是⊙O的切线；(5分)

(2)已知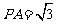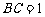，，求⊙O的半径．(5分)

21．(本题满分10分)

某班6名同学组成了一个“帮助他人，快乐自己”

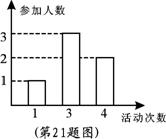的体验小组．他们约定一学期每人至少参加一次公益活

动．学期结束后，他们参加公益活动的统计图如右．

(1)这个体验小组一学期参加公益活动的人均次数

是　 ▲　 　次；(4分)

(2)从这6名同学中任选两名同学(不考虑先后顺序)，他们参加公益活动的次数恰好相等的概率是多少？(6分)

20．(本题满分8分)

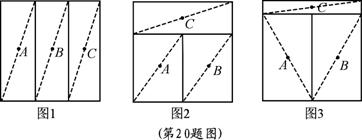
三个牧童A、B、C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时他们所需走的最大距离(看守点到本区域内最远处的距离)相等．按照这一原则，他们先设计了一种如图1的划分方案：把正方形牧场分成三块相等的矩形，大家分头守在这三个矩形的中心(对角线交点)，看守自己的一块牧场．

过了一段时间，牧童B和牧童C又分别提出了新的划分方案．

牧童B的划分方案如图2：三块矩形的面积相等，牧童的位置在三个小矩形的中心．

牧童C的划分方案如图3：把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个人所需走的最大距离相等．

请回答：

(1)牧童B的划分方案中，牧童　 ▲　 (填A、B或C)在有情况时所需走的最大距离较远；(3分)

(2)牧童C的划分方案是否符合他们商量的划分原则？为什么？(提示：在计算时可取正方形边长为2)(5分)

19．(本题满分6分)　　　　　　　　　　

已知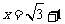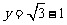：，，求下列各式的值.

(1)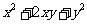；(3分)　 (2)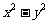．(3分)

18．在平面直角坐标系中，有A(3，－2)，B(4，2)两点，现另取一点C(1，n)，

当n =　　 ▲　　 时，AC + BC的值最小．

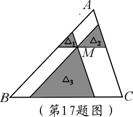
17．如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△₁、△₂、△₃(图中阴影部分)的面积分别是4，9和49．则△ABC的面积是　　 ▲　　 ．

16．对于任意两个实数对(a，b)和(c，d)，规定：当且仅当a＝c且b＝d时，

(a，b)=(c，d)．定义运算“”：(a，b)(c，d)=(ac－bd，ad+bc)．

若(1，2)(p，q)=(5，0)，则p＝　　 ▲　　 ，q＝　　 ▲　　 ．