
8.一个函数的图象关于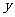 轴成轴对称图形时,称该函数为偶函数. 那么在下列四个函数①
轴成轴对称图形时,称该函数为偶函数. 那么在下列四个函数①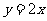 ;②
;②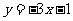 ;③
;③ ;④
;④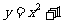 中,偶函数是 (填出所有偶函数的序号).
中,偶函数是 (填出所有偶函数的序号).
7.如图3,已知 ,∠1=130o,∠2=30o,则∠C= .
,∠1=130o,∠2=30o,则∠C= .
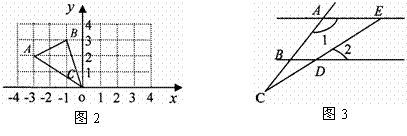
6.如图2,△ABC向右平移4个单位后得到△A′B′C′,则A′点的坐标是 .
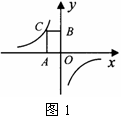
5.如图1,已知点C为反比例函数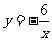 上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC的面积为 .
上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC的面积为 .
4. 一个圆锥的母线长为5cm,底面圆半径为3 cm,则这个圆锥的侧面积是 cm2(结果保留
一个圆锥的母线长为5cm,底面圆半径为3 cm,则这个圆锥的侧面积是 cm2(结果保留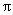 ).
).
3.已知△ABC中,BC=6cm,E、F分别是AB、AC的中点,那么EF长是 cm.
2.因式分解: .
.
1.3的倒数等于 .
25.解:(1)依条件有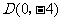 ,
,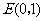 .
.
 由
由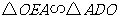 知
知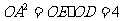 .
.
∴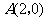 由
由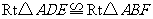 得
得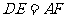 .
.
∴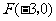 .
.
将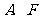 的坐标代入抛物线方程,
的坐标代入抛物线方程,
得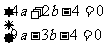
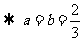 .
.
∴抛物线的解析式为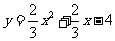 .····································································· 3分
.····································································· 3分
(2)设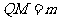 ,
,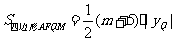 ,
, .
.
∴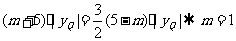
设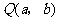 ,则
,则
∴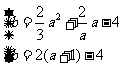
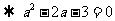 ,
,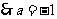 (舍去
(舍去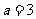 )
)
此时点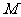 与点
与点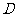 重合,
重合, ,
,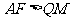 ,
,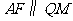 ,
,
则 为等腰梯形.······························································································· 3分
为等腰梯形.······························································································· 3分
(3)在射线 上存在一点
上存在一点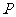 ,在射线
,在射线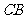 上存在一点
上存在一点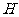 .
.
使得 ,且
,且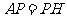 成立,证明如下:
成立,证明如下:
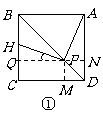
当点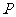 如图①所示位置时,不妨设
如图①所示位置时,不妨设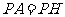 ,过点
,过点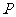 作
作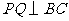 ,
, ,
,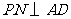 ,垂足分别为
,垂足分别为 .
.
 若
若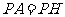 .由
.由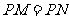 得:
得:
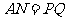 ,
,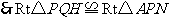
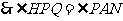 .
.
又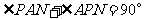

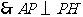 .············································································································· 2分
.············································································································· 2分
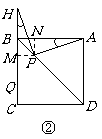
当点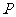 在如图②所示位置时,
在如图②所示位置时,
过点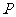 作
作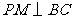 ,
,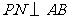 ,
,
垂足分别为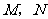 .
.
同理可证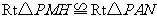 .
.
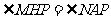 .
.
又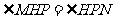 ,
,
 ,
,
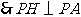 .············································································································· 1分
.············································································································· 1分
当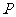 在如图③所示位置时,过点
在如图③所示位置时,过点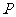 作
作 ,垂足为
,垂足为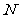 ,
,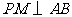 延长线,垂足为
延长线,垂足为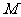 .
.
同理可证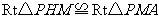 .
.
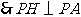 .············································································································· 1分
.············································································································· 1分
注意:分三种情况讨论,作图正确并给出一种情况证明正确的,同理可证出其他两种情况的给予4分;若只给出一种正确证明,其他两种情况未作出说明,可给2分,若用四点共圆知识证明且证明过程正确的也没有讨论三种情况的.只给2分.
24.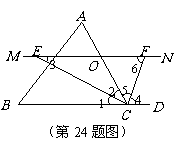 解:(1)
解:(1)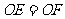 .
.
其证明如下:
∵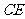 是
是 的平分线,
的平分线,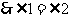 .
.
∵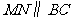 ,∴
,∴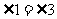 .
.
∴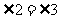 .
.
∴ .
.
同理可证 .
.
∴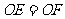 .······················································· 3分
.······················································· 3分
(2)四边形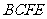 不可能是菱形,若
不可能是菱形,若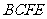 为菱形,则
为菱形,则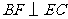 ,而由(1)可知
,而由(1)可知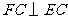 ,在平面内过同一点
,在平面内过同一点 不可能有两条直线同垂直于一条直线.············································································· 3分
不可能有两条直线同垂直于一条直线.············································································· 3分
(3)当点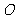 运动到
运动到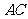 中点时,
中点时,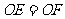 ,
,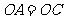 ,则四边形
,则四边形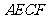 为
为 ,要使
,要使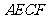 为正方形,必须使
为正方形,必须使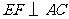 .
.
∵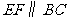 ,∴
,∴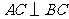 ,∴
,∴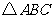 是以
是以 为直角的直角三角形,
为直角的直角三角形,
∴当点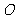 为
为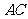 中点且
中点且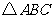 是以
是以 为直角的直角三角形时,
为直角的直角三角形时,
四边形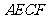 是正方形.····························································································· 3分
是正方形.····························································································· 3分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com