
23.(本题满分14分)
已知:如图,抛物线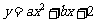 与
与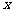 轴的交点是
轴的交点是 、
、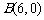 ,与
,与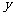 轴的交点是C.
轴的交点是C.
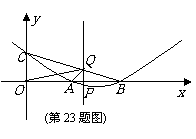 (1)求抛物线的函数表达式;(4分)
(1)求抛物线的函数表达式;(4分)
(2)设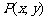 (0<
(0<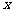 <6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当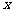 取何值时,线段PQ的长度取得最大值?其最大值是多少?(5分)
取何值时,线段PQ的长度取得最大值?其最大值是多少?(5分)
②是否存在这样的点P,使△OAQ为直角三角 形?若存在,求出点P的坐标;若不存在,请说明理由.(5分)
22. (本题满分12分)
已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形
ABCD边AB、BC、DA上,AE=2.
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;(4分)
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式
表示);(4分)
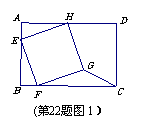
 (3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.(4分)
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.(4分)
21. (本题满分12分)
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
|
|
甲 |
乙 |
|
进价(元/件) |
15 |
35 |
|
售价(元/件) |
20 |
45 |
(注:获利=售价-进价)
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?(6分)
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案? 并直接写出其中获利最大的购货方案.(6分)
20.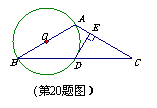 (本题满分12分)
(本题满分12分)
已知:如图,在⊿ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作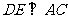 于点E.
于点E.
(1)请说明DE是⊙O的切线;(6分)
(2)若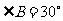 ,AB=8,求DE的长.(6分)
,AB=8,求DE的长.(6分)
19.(本题满分10分)
甲布袋中有三个红球,分别标有数字1,2,3;乙布袋中有三个白球,分别标有数字2,3,4.这些球除颜色和数字外完全相同.小亮从甲袋中随机摸出一个红球,小刚从乙袋中随机摸出一个白球.
(1)用画树状图(树形图)或列表的方法,求摸出的两个球上的数字之和为6的概率;
(5分)
(2)小亮和小刚做游戏,规则是:若摸出的两个球上的数字之和为奇数,小亮胜;否则,小刚胜.你认为这个游戏公平吗?为什么?(5分)
18.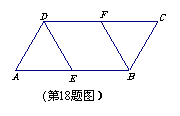 (本题满分10分)
(本题满分10分)
已知:如图,□ABCD中,E、F分别是边AB、CD的中点.
(1)求证:四边形EBFD是平行四边形;(5分)
(2)若AD=AE=2,∠A=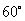 ,求四边形EBFD的周长.(5分)
,求四边形EBFD的周长.(5分)
17.(本题满分16分,每小题8分)
(1)先化简,再求值: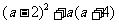 ,其中
,其中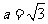 ;
;
(2)解方程: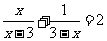 .
.
16.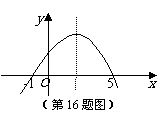 如图为二次函数
如图为二次函数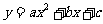 的图象,在下列结论中:①
的图象,在下列结论中:①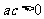 ;②方程
;②方程 的根是
的根是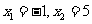 ;③
;③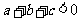 ;④当
;④当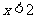 时,y随着x的增大而增大.正确的结论有_******(请写出所有正确结论的序号).
时,y随着x的增大而增大.正确的结论有_******(请写出所有正确结论的序号).
15.如图,将一块含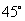 角的直角三角尺ABC在水平桌面上绕点B按顺时针方向旋转到
角的直角三角尺ABC在水平桌面上绕点B按顺时针方向旋转到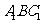 的位置,若AB=8cm,那么点A旋转到
的位置,若AB=8cm,那么点A旋转到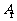 所经过的路线长为_****** cm.(结果保留
所经过的路线长为_****** cm.(结果保留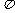 )
)
14.甲、乙两支足球队,每支球队队员身高数据的平均数都是1.70米,方差分别为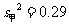 ,
,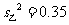 ,其身高较整齐的球队是_****** 队.
,其身高较整齐的球队是_****** 队.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com