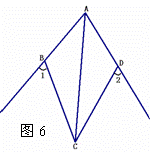
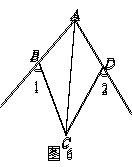
18．证明：∵AC平分∠BAD

　　　　 ∴∠BAC＝∠DAC．

　　　　 　∵∠1＝∠2

　　 ∴∠ABC＝∠ADC．

在△ABC和△ADC中

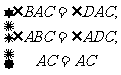
∴△ABC≌△ADC(AAS)．……………………8分

∴AB＝AD．……………………10分

(其他不同证法，参照以上标准评分)

18．(满分10分)

如图6，已知AC平分∠BAD，∠1＝∠2，求证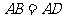：．全品中考网 　全品　 中考网

17．(1)解：3x－x＞2

2x＞2

x＞1．……………………6分

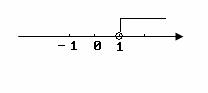
……………………8分

(2)解：设先安排整理的人员有x人，依题意得，

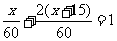　　　　 ……………………4分

　　 解得，　x＝10．

答：先安排整理的人员有10人．……………………8分

17．(每小题8分，共16分)

(1)解不等式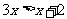：，并在数轴上表示解集．

(2)整理一批图书，如果由一个人单独做要花60小时．现先由一部分人用一小时整理，随后增加15人和他们一起又做了两小时，恰好完成整理工作．假设每个人的工作效率相同，那么先安排整理的人员有多少人？

16．(1)解：原式＝4－1+2

　　　　　 ＝3+2

　　　　　 ＝5．……………………7分

(2)解：原式＝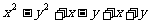

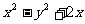　　　　　 ＝．……………………7分

16．(每小题7分，共14分)

(1)计算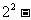：5×+．

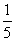(2)化简：．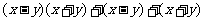

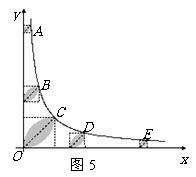
15． 13π－26[解析]本题考查的是反比例函数和圆的有关计算.首先根据能够整除16的正整数,求出图像上的5个整数点分别为(1,16),(2,8),(4,4),(8,2),(16,1),其次利用扇形面积公式求弓形面积,即每个橄榄形面积的一半.当点P位于点(4,4)时,S_橄榄型＝2×(－S_{等腰直角三角形})＝8π－16,其余四个计算方法同上.它们的面积从左到右分别为π－1,2π－4, 2π－4, π－1.所以橄榄形面积总和为13π－26. 本题容易错误的地方是在不理解什么是整数点的情况下无法求出A、B、C、D、E五点的整数点坐标，这也就是本题的难点所在.

15．已知A、B、C、D、E是反比例函数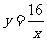(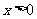)图象上五个整数点(横、纵坐标均为整数)，分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图5所示的五个橄榄形(阴影部分)，则这五个橄榄形的面积总和是　　　 (用含π的代数式表示)．

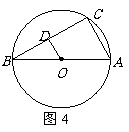
14. 2[解析]本题考查的是垂径定理和平行线、圆周角性质.因为AB是直径,所以它所对的圆周角为直角,再根据两条直线平行,同位角相等,所以OD⊥BD,根据垂径定理,可知,D为BD的中点,所以BC＝2BD＝2.

14． 如图4，AB是⊙O的直径，点C在⊙O上 ，OD∥AC，交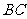于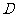．若BD＝1，则BC的长为

　　　　 ．