
26.如图 ,点
,点 ,
, 的坐标分别为(2,0)和(0,
的坐标分别为(2,0)和(0, ),将
),将 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转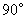 后得
后得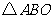 ,点
,点 的对应点是点
的对应点是点 ,点
,点 的对应点是点
的对应点是点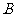 .
.
(1)写出 ,
,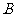 两点的坐标,并求出直线
两点的坐标,并求出直线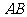 的解析式;
的解析式;
(2)将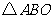 沿着垂直于
沿着垂直于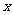 轴的线段
轴的线段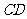 折叠,(点
折叠,(点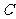 在
在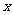 轴上,点
轴上,点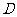 在
在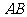 上,点
上,点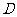 不与
不与 ,
,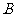 重合)如图
重合)如图 ,使点
,使点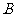 落在
落在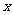 轴上,点
轴上,点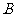 的对应点为点
的对应点为点 .设点
.设点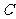 的坐标为(
的坐标为(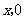 ),
),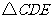 与
与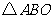 重叠部分的面积为
重叠部分的面积为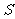 .
.
i)试求出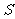 与
与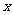 之间的函数关系式(包括自变量
之间的函数关系式(包括自变量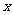 的取值范围);
的取值范围);
ii)当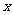 为何值时,
为何值时,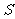 的面积最大?最大值是多少?
的面积最大?最大值是多少?
iii)是否存在这样的点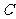 ,使得
,使得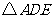 为直角三角形?若存在,直接写出点
为直角三角形?若存在,直接写出点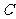 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
25.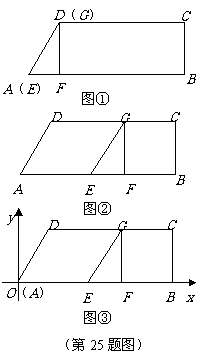 如图
如图 ,在梯形
,在梯形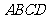 中,
中,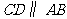 ,
,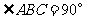 ,
,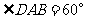 ,
,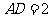 ,
,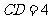 .另有一直角三角形
.另有一直角三角形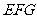 ,
,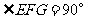 ,点
,点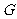 与点
与点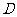 重合,点
重合,点 与点
与点 重合,点
重合,点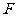 在
在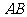 上,让
上,让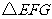 的边
的边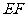 在
在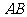 上,点
上,点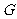 在
在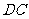 上,以每秒1个单位的速度沿着
上,以每秒1个单位的速度沿着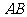 方向向右运动,如图
方向向右运动,如图 ,点
,点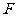 与点
与点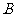 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为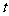 秒.
秒.
(1)在上述运动过程中,请分别写出当四边形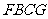 为正方形和四边形
为正方形和四边形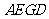 为平行四边形时对应时刻
为平行四边形时对应时刻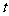 的值或范围;
的值或范围;
(2)以点 为原点,以
为原点,以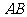 所在直线为
所在直线为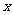 轴,过点
轴,过点 垂直于
垂直于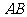 的直线为
的直线为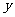 轴,建立如图
轴,建立如图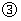 所示的坐标系.求过
所示的坐标系.求过 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)探究:延长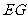 交(2)中的抛物线于点
交(2)中的抛物线于点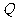 ,是否存在这样的时刻
,是否存在这样的时刻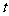 使得
使得 的面积与梯形
的面积与梯形 的面积相等?若存在,求出
的面积相等?若存在,求出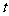 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
24.某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节,感受冰雕艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车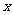 辆,租车总费用为
辆,租车总费用为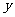 元.
元.
|
|
甲种客车 |
乙种客车 |
|
载客量(人/辆) |
45 |
30 |
|
租金(元/辆) |
280 |
200 |
(1)求出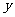 (元)与
(元)与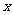 (辆)之间的函数关系式,指出自变量的取值范围;
(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?
23.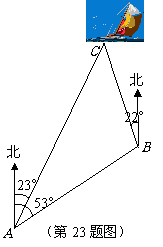 一艘小船从码头
一艘小船从码头 出发,沿北偏东
出发,沿北偏东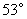 方向航行,航行一段时间到达小岛
方向航行,航行一段时间到达小岛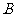 处后,又沿着北偏西
处后,又沿着北偏西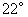 方向航行了10海里到达
方向航行了10海里到达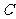 处,这时从码头测得小船在码头北偏东
处,这时从码头测得小船在码头北偏东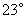 的方向上,求此时小船与码头之间的距离(
的方向上,求此时小船与码头之间的距离(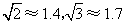 ,结果保留整数).
,结果保留整数).
22.海峡两岸实现“三通”后,某水果销售公司从台湾采购苹果的成本大幅下降.请你根据两位经理的对话,计算出该公司在实现“三通”前到台湾采购苹果的成本价格.

21.在改革开放30年纪念活动中,某校学生会就同学们对我国改革开放30年所取得的辉煌成就的了解程度进行了随机抽样调查,并将调查结果绘制成如图所示的统计图的一部分.
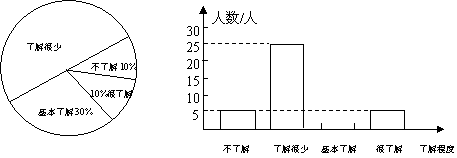
根据统计图中的信息,解答下列问题:
(1)本次抽样调查的样本容量是___________.调查中“了解很少”的学生占_________%;
(2)补全条形统计图;
(3)若全校共有学生1300人,那么该校约有多少名学生“很了解”我国改革开放30年来取得的辉煌成就?
(4)通过以上数据分析,请你从爱国教育的角度提出自己的观点和建议.
20.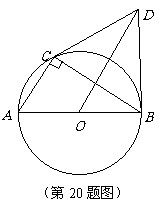 如图,
如图,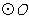 是
是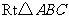 的外接圆,点
的外接圆,点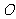 在
在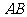 上,
上,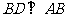 ,点
,点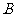 是垂足,
是垂足,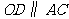 ,连接
,连接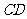 .
.
求证: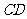 是
是 的切线.
的切线.
19.袋中装有除数字不同其它都相同的六个小球,球上分别标有数字1,2,3,4,5,6.
(1)从袋中摸出一个小球,求小球上数字小于3的概率;
(2)将标有1,2,3数字的小球取出放入另外一个袋中,分别从两袋中各摸出一个小球,求数字之和为偶数的概率.(要求用列表法或画树状图求解)
18.在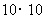 的网格纸上建立平面直角坐标系如图所示,在
的网格纸上建立平面直角坐标系如图所示,在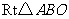 中,
中,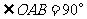 ,且点
,且点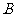 的坐标为
的坐标为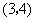 .
.
(1)画出 向左平移3个单位后的
向左平移3个单位后的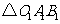 ,写出点
,写出点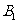 的坐标;
的坐标;
 (2)画出
(2)画出 绕点
绕点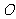 顺时针旋转
顺时针旋转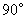 后的
后的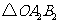 ,并求点
,并求点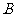 旋转到点
旋转到点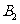 时,点
时,点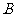 经过的路线长(结果保留
经过的路线长(结果保留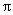 )
)
17.先化简,再求值: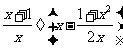 ,其中
,其中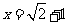 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com