
教学:夯实基础,提高实效
1.不实现象:(1)追求一步到位。(2)难度盲目拔高。(3)迷信大容量。(4)迷信快节奏。
(5)少数人表现,多数人当观众。(6)表面上热闹。(7)课堂上无事可干,或干不了。(8)心游他方。
﹡﹡教师困惑:方向是什么?方向会不会变?讲了做了很多,似乎没有多大用。做了懂了1000道,第1001道可能还不会做。是深挖?广猎?还是重在探究与能力?
教学:以学生为本,为发展服务。
﹡﹡若能真按中考评价所倡导的方向去复习,则既能减轻学生负担又能提高学生素质。
了解学生,以从学生实际出发为要领
美国著名教育心理学家奥苏伯尔:“如果我不得不将所有的教育心理学原理还原为一句话的话,我将会说,影响学习的最重要因素是学生已经知道了什么,根据学生的原有知识状况进行教学”。
怎样了解?通过各种学习活动中的学生表现来了解。
例1(Ⅰ)(青海)化简: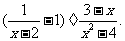 (Ⅱ)(青岛)用配方法解方程:x
(Ⅱ)(青岛)用配方法解方程:x - 2x -2 = 0.
- 2x -2 = 0.
例2(Ⅰ)下列四个三角形中,与右图中的三角形相似的是( ).
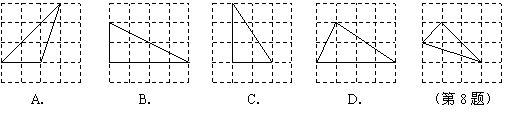
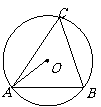
(Ⅱ)如图,△ABC是⊙D的内接三角形,点C是优弧AB上一点,
设∠OAB=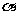 ,∠C=
,∠C= .
.
(1)当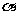 =35°时,求
=35°时,求 的度数;(2)猜想
的度数;(2)猜想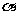 与
与 之间的关系,并给予证明.
之间的关系,并给予证明.
随说:双基理解、掌握了没有?有多少学生掌握了?未掌握的困难所在?
在这些活动中,学生有怎样的心智活动表现和情绪表现?追溯到最初未掌握的地方,并从这里开始。当前教学最大的困难之一,是一些学生讨厌学习。
遵循规律,以促进学生发展为要务
(1)不要干扰学生的数学思维(章建跃老师的建议与所模拟的学生的心理活动)
①思维需要合适的问题情景--老师,我不是三岁的孩子,也不是数学家,请在设置问题情景时,能够让我“跳一跳,够得着”;
②思维从问题开始--老师,不要总是您提出问题让我们回答,请给我提问的机会;
③独立思考需要安静的环境--老师,提出问题后,您可以先看一看窗外的风景,让我先理解一下题意,先让我自己独立思考一下,您为了不让我们走弯路而“喋喋不休”的引导,实在是对我们思维的干扰;
④有深度的思维需要充分的时间--老师,提出问题后,请给我思考的时间,不要马上让我回答,请您耐心点,别逼我;
⑤让学生完成关键的概括活动--老师,有了这些具体例子为基础,我也能概括出一般的规律,请把发现的机会让给我;
⑥数学思维是以概念的发生发展过程为线索的,要体现前后一致的思想方法--老师,如果我理解了概念,通过解答一定量的题目,让我有反思解题过程的机会,从中总结概括基本思想方法,那么“什么样的题目我都能对付”,请不要用“题型”限制我。
(2)“最近发展区”及其对教学的意义
“最近”――最近学生的原有基础,教学活动开展的起点。目标明确,目标准确。
①在新课程推进的背景下,起点应该有新的内涵:起点不是一维的,而是三维的,即不但有“知识与能力”的起点,还应该有“过程与方法”和“情感、态度与价值观”的起点。
②学生是有差异的,因此,应该关注大部分学生起点,同时在教学中,尽可能关注每一位学生。
③如果能把学生原来的“相异构想”( 与正确的概念及思维方法大相径庭的想法)显现出来,与正确的认识“碰撞”,再放入学生的脑中,这样的教学才是启发。才是有意义的学习。否则,如果仅仅告诉学生什么是正确的,而“相异构想”尚未得到纠正。
﹡﹡出错是正常现象――宽容。课堂本来就是出错的场所。纠正错误正是走向真理的开始――从错误中学习。暴露自己的错误。让学生展现所有错误――不仅仅是展现正确好的。
 例3 观察函数y=2x-5的图像,回答下列问题:
例3 观察函数y=2x-5的图像,回答下列问题:
(1)x取何值时,2x-5=0?
(2)x取何值时,2x-5>0?
(3)x取何值时,2x-5<0?
(4)x取何值时,2x-5>3?
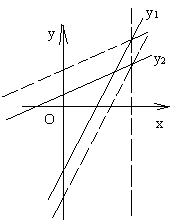
练习:如图,是函数y=-2x-6的图像,
看图回答问题:
(1)当x 时,-2x -6>0?(2)当x 时,-2x - 6<0?
A:x>3,-2x-6>0?,…… B:x<3,-2x-6>0?,……
T:同意B的举手?-2x-6就是谁? S:y; T:有没有其他方法求解?
反思:(1)A只是形式上的“学会了”,所以不会变通。(2)举手的办法不是确定真理的标准。
(3)有了一致的认同,并不一定懂了。(4)这里的本质与重点是有没有其他的求解方法吗?用函数观点(本质上不是方法层面)观察一元一次不等式、一元一次方程及二元一次方程组时,建立了一个从整体观察局部、数形结合的方法:解不等式时,只要求解相应的方程就可以了(确定界点),以后只要观察图像便能解决问题。即用方程获得精确的解,数形结合的方法获得求解不等式的思路,同时也避免了解不等式变号可能出现的错误,还避免了三次重复地做一个相似的问题。
 (5)转化:x轴向上平移3个单位。
(5)转化:x轴向上平移3个单位。
拓展:如下图,已知:y1=2x-5和y2=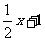 ,请回答下列问题:
,请回答下列问题:
x取何值时,y1=y2? x取何值时,y1>y2?
x取何值时,y1<y2? x取何值时,y1-y2>3?
S:(学生几乎全部用的是解的方法)
T:(2)(3)还有没有其他方法?
反思:(1)学生明显地习惯于代数方法,并认为这样才能准确地
确定问题的解?而笼统地认为图像法并并提供解决问题的技术。
(2)用函数观察,这里解不等式问题意味着什么?似乎未明晰。
(3)朝哪里拓展?数形结合的解决问题;
(4)是更有意义的。转化:y1>y2+3或y1-3>y2.
④“过程与方法”的效果往往不能即刻凸现,并且往往不是显性的,而是隐性的;要增强计划性。
⑤哪些是已经懂了的,哪些是易懂的,哪些是困难的,哪些是易误解的,哪些是能力的生长点,在易误解的、困难的、生长点上着力是提高效率的关键。知道的不讲,易懂的少讲,难懂的、有价值的地方多花力气。
⑥造成认知冲突。只有产生认知冲突时,问题才对思维的发展有益。
⑦让学生展现自己的才华,而不是教师展示自己的才智。
(3)让学生学会思考、学会探究。 探究精神是课堂的灵魂,唯有探究才能培养思想者和批判者,没有探究的教学只能是训练。探究学习的意蕴:思考、质疑、批判、欣赏、创新。让探究成为课堂教学的常态。
(4)提升学生的学习体验:激发情趣。
良好的态度与良好的师生关系:①宽容,接纳学生;②重视,尊重学生;③相信,依靠学生。
建立“自由、民主、宽松、和谐”的课堂文化。关注学生的感受,让学生觉得:学习数学是有趣或值得做的事情。
例4 教师对学生影响的两个例子:
一位留美博士、20年前的学生回校探望老师时说:“您当年课上的‘挖小妙’(挖掘问题中小小的妙处,注意每个细节)20年来我一直在用着,天天用,而且越用越管用!”
另一位千万富翁的企业家在教师节给老师的贺卡中写道:“您的‘瞄准靶心--射击’(看问题要把握中心、抓住本质)一直影响着我!您在课堂上教给我们的思考问题的方法,让我们一辈子受用无穷。”
(5)突出学生的主体作用。
一位特级教师给自己立下了“三不教”原则,即:①凡学生自己看书能懂,不教;②凡看书不懂但自己想想能够弄懂,不教;③想想也不懂但经过学生之间讨论能懂,也不教。
江苏洋思“之教”三点:
①教的内容应该是学生自学后还不能掌握的地方,即自学中暴露出来的主要倾向性的疑难问题,对学生通过自己已掌握的,一律不教。
②教的要求,不就题讲题,只找出答案,而要寻找出规律,真正让学生知其所以然。还要引导学生预防运用时可能出现的毛病。
③教的方式都让已掌握的学生先讲(即使倾向性问题,也可能有人会),如学生讲对了,教师肯定,不必重复;讲得不完整、达不到深度的,教师要补充;讲错了的,教师则要更正。这样,教师讲的时间就少了,一般不超过5分钟,但能通过补充、更正的方式达到解决疑难问题的目的。
评价:为学生展示学习成果提供舞台
合理、科学地评价学生;使不同学生得到不同的发展表现;有效控制难度,努力降低难度;
 努力控制文字量,尽量减少文字量。
努力控制文字量,尽量减少文字量。
评价方向:基础性,层次性为主体。加强以基本功为重点的基本素养
的考查。
样卷表现:以不同形式,强化对双基的考查。
 例5(Ⅰ)二次函数
例5(Ⅰ)二次函数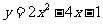 的最小值是
.
的最小值是
.
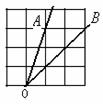
(Ⅱ)如图,在正方形网格中,∠AOB的正切值是 .
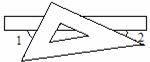
(Ⅲ)如图,某同学在课桌上无意中将一块三角板叠放在直尺上,
他发现∠1+∠2= 度.
说明:中考试卷中,基础性的、常见试题应当占有较大的比重.
同时,出现少量有点创意、难度不大的小题是必需的,它可引导教学更灵活地加强基础内容的教学,也可以对学生施以更客观的评价。选择题往往能对概念等的理解施以有效考查,填空题往往能对简单技能的掌握情况施以有效考查,因此,选择题、填空题等是考查简单双基的主体。
26.如图14,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
25.如图13,直角梯形ABCD和正方形EFGC的边BC、CG在同一条直线上,AD∥BC,AB⊥BC于点B,AD=4,AB=6,BC=8,直角梯形ABCD的面积与正方形EFGC的面积相等,将直角梯形ABCD沿BG向右平行移动,当点C与点G重合时停止移动.设梯形与正方形重叠部分的面积为S.
(1)求正方形的边长;
(2)设直角梯形ABCD的顶点C向右移动的距离为x,求S与x的函数关系式;
(3)当直角梯形ABCD向右移动时,它与正方形EFGC的重叠部分面积S能否等于直角梯形ABCD面积的一半?若能,请求出此时运动的距离x的值;若不能,请说明理由.
24.某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图12所表示的一次函数.
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
23.如图11,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若DE=3,⊙O的半径为5,求BF的长.
22.根据规划设计,某市工程队准备在开发区修建一条长300米的盲道.铺设了60米后,由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10米,结果共用了8天完成任务,该工程队改进技术后每天铺设盲道多少米?
21.小刚和小明玩“石头”、“剪子”、“布”的游戏,游戏的规则为:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”,若两人所出手势相同,则为平局.
(1)玩一次小刚出“石头”的概率是多少?
(2)玩一次小刚胜小明的概率是多少?用列表法或画树状图法加以说明.
20.为了加快城市经济发展,某市准备修建一座横跨南北的大桥.如图10所示,测量队在点A处观测河对岸水边有一点C,测得C在北偏东60°的方向上,沿河岸向东前行30米到达B处,测得C在北偏东45°的方向上,请你根据以上数据帮助该测量队计算出这条河的宽度.(结果保留根号)
19.某校开展以“庆国庆60周年”为主题的艺术活动,举办了四个项目的比赛.它们分别是:A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九年(一)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图9中所给出的信息解答下列问题:
(1)求出参加绘画比赛的学生人数占全班总人数的百分比;
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次活动中参加演讲和唱歌的学生共有多少人?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com