
5、在初中数学学习过程中,老师或家长对我的态度是( )(可以填两项)
A、经常鼓励我 B、很少鼓励我 C、经常批评我
D、经常帮助我 E、很少帮助我 F、很少关注我
G、其他: .
4、在初中三年各阶段,我的数学学习成绩( )
A、总是处于上游 B、多数处于中上游 C、多数处于中游
D、多数处于中下游 E、多数处于下游
3、我对我的数学老师喜好程度?①初一时( );②初二时( );③初三时( ).
A、非常喜欢 B、比较喜欢 C、一般 D、不喜欢
E、原因是:① ;② ;③ .
2、我觉得数学( )
A、非常有趣 B、比较有趣 C、不怎么有趣 D、枯燥无味 G、其它: .
亲爱的同学,请你如实地完成下面的问卷和试题;我们将用于教育科学与心理学调查,并不针对你或老师进行评价,谢谢你的合作。
1、我是( )
A、男生 B、女生
教育案例:有位家长带着读初一的女儿去作教育心理咨询:我这女儿听到过的东西一遍就能记住,上课老师讲的东西就能记住,但背课文很慢、数学公式老记不住,你说怪不怪?究竟是什么原因? 家长例举的这个案例并不奇怪,因为她属于典型的听觉学习型,听觉注意力和听觉记忆力很强,善于倾听,听过就能记住,但视觉注意力和视觉记忆力很弱,看过的东西不容易记住。 研究发现,人的学习类型分为:视觉学习型、听觉学习型、听觉·视觉综合学习型、视觉·运动综合学习型、视觉·触觉综合学习型等。视觉学习型:喜欢看,视觉注意力视觉记忆力都非常棒,看过就能记住,做作业考试比较细心认真,但听课效率不够高;听觉学习型:喜欢听,听过就能记住,听课效率相对较好,但在背课文、记单词方面则较弱,容易看错题、看错数字、符号,甚至漏看漏做题等;视觉听觉综合型,则视觉听觉注意力记忆力平衡发展,两种感官参加识记,听课、学习效果较好;视觉·运动综合学习型,在学习时喜欢配上一些动作,如摇头晃脑地读书背书、边走边看书、做作业考试时喜欢转笔等等;视觉·触觉学习型,喜欢东摸摸西摸摸,什么都想用手去感知,喜欢做实验,做到摸过的就特别容易理解,容易记住。 在此案例中,教育心理专家给这位女生做了全面的学习能力和学习类型测评,发现她听觉注意力记忆力超强,而视觉注意力视觉记忆力超弱。于是帮助她的方案是:一方面有针对性地进行视觉注意力和视觉记忆力强化训练,一方面是一边听录音,一边英语单词或英语课文,听和看相结合来提高背课文、背单词的速度。经过40多天的训练,这位家长打电话告知:孩子背课文、记单词的速度快多了,平时做作业看错、写错现象也减少,月考成绩明显进步。 所以,了解孩子的学习类型,指导孩子用适合自己学习类型的学习方法来学习,对提高学习效率和学习成绩很有帮助。
(一) 教学:源于反思,成于改进
﹡﹡有所设想,有所尝试,有所反思,不断改进
例12(苏州)初三数学课本上,用“描点法”画二次函数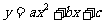 的图象时,列了如下表格:
的图象时,列了如下表格:
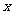 |
… |
 |
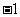 |
0 |
1 |
2 |
… |
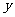 |
… |
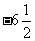 |
 |
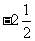 |
 |
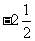 |
… |
根据表格上的信息回答问题:该二次函数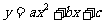 在
在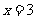 时,
时, .
.
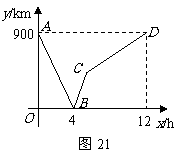 例13(南京)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为
例13(南京)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为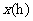 ,两车之间的距离为
,两车之间的距离为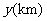 ,图中的折线表示
,图中的折线表示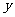 与
与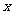 之间的函数关系.
之间的函数关系.
根据图象进行以下探究:
信息读取
(1)甲、乙两地之间的距离为 km;
(2)请解释图中点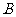 的实际意义;
的实际意义;
图象理解
(3)求慢车和快车的速度;
(4)求线段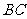 所表示的
所表示的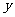 与
与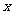 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量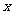 的取值范围;
的取值范围;
问题解决
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
随说:如何教才能使效果最大化?――长远与全体为重。
•在知识生长点处引入; 在知识结合点处展开;
•在知识关键点处引伸; 在能力提高点处设疑;
•在有价值处思考讨论; 在困难处点拨与分析。
(二) 评价:考数学素养,非展示作品
问题与困惑:(1)辅助线问题、删去内容问题、新增内容问题、计算器问题、带好备用纸片等问题等怎样处理?(2)有人认为:近几年中考有看重不等式,看轻方程趋势,对否?二次函数应用题近年考得很少,是否应当加强?――重要的是建模,而点落何处,应由问题自然引出。(3)基础(基本核心主干)与探究等(基础外)的比例如何?基础:探究等的比例约7:3。探究等也分为中等与较高两个层次。
样卷表现:对探究能力的考查受到高度重视
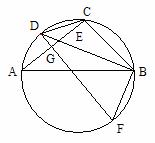 例11 (Ⅰ) 如图,在△ABC的外接圆中,BD平分∠ABC,DB⊥FB, D、F在△ABC的外接圆上,连接DF交AC于G.
例11 (Ⅰ) 如图,在△ABC的外接圆中,BD平分∠ABC,DB⊥FB, D、F在△ABC的外接圆上,连接DF交AC于G.
(1)根据图中已知条件,试写出三个不同类型的正确结论(不再添加辅助线和字母);
(2) 若DF=9,sin∠DBC=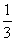 ,求AC的长.
,求AC的长.
 (Ⅱ)已知:如图,△ABC是等腰直角三角形,D为斜边AB上的任意一点(不与点A、B重合),连接CD,作EC⊥DC,且EC = DC,连接AE.
(Ⅱ)已知:如图,△ABC是等腰直角三角形,D为斜边AB上的任意一点(不与点A、B重合),连接CD,作EC⊥DC,且EC = DC,连接AE.
(1)求证:∠E+∠ADC=180°;
(2)猜想:当点D在何特殊位置时,四边形AECD是何种特殊四边形?说明理由.
说明:开放与探索是发展学生创新思维能力的两大方面,这既是数学课程的潜在目标,又是数学独特教育功能的重要方面,因而中考中理应关注并加强。这一直是我们所关注的重要内容,教师们应予以高度重视。
(一) 教学:激发与启发,引导与指导
﹡﹡数学之妙在于理,教学之道在于度﹡﹡
1.不正现象:(1)课堂教学→“题型教学”→“刺激--反应”训练。有的教师试图通过“题型教学”穷尽“题型”,幻想通过“题型”的机械重复、强化训练,让学生掌握对应的“特技”和“动作要领”而提高考试分数。对具有普适意义的、迁移能力强的“根本大法”--数学思想方法的教学,却因其不是“立竿见影”,需要较长时间的坚持才能奏效,是一种潜移默化、润物无声的“慢工”,被有些老师判为“不实惠”而得不到应有的渗透、提炼和概括。结果是在稍有变化的情境中,因为没有数学思想方法的支撑,“特技”失灵,“动作”变形,灵活应用数学知识解决问题的能力成为“泡影”。 “讲过练过的不一定会,没讲没练的一定不会”。
(2)例题教学替代概念的概括过程。认为“应用概念的过程就是理解概念的过程”。殊不知没有概括过程必然导致概念理解的先天不足,没有理解的应用是盲目的应用。结果不仅“事倍功半”,而且“功能僵化”--面对新情境时无法“透过现象看本质”,难以实现概念的正确、有效应用,质量效益都无保障。
(3)能力异化(技能化)问题。――尽量使之程序化、技能化。“一个方法,三项注意事项”。
(4)将复习课上成压缩后的新授课,或上成单纯的练习课。理解变成了记忆,探究变成了听懂。
(5)按照现成资料,无删无增,照本宣科,看题讲题。
2.办法:(1)“不断回到概念去,从基本概念出发思考问题、解决问题”,回到基本思想,回到基本想法;(2)加强概念的联系性,从概念的联系中寻找解决问题的新思路。(3)“题型”、与“题型”对应的技巧是雕虫小技,无法穷尽,“巧”是教不会的,要靠学生自己琢磨;(4)追求解决问题的“根本大法”--基本概念所蕴含的思想方法,要强调思想指导下的操作。(5)整体把握,复习引入,思考延伸课外,引发课后的讨论。(6)防止水平下降。坚持为理解而教,为发展而教。(7)自然的延伸。(8)“举一反三”,“举三反一”。(9)“控制”自己的讲解。
3.有效教学的铁律:
(1)先学后教--以学定教
(2)先教后学--以教导学
(3)“温故知新”--学会了才有兴趣;重新认识,有所提高。
4.其他观念:多与少(量)。粗与细(讲授)。小与大(方法)。远与近(目标)。高与低(观点)。理与例(内容)。明与暗(思想)。善与恶(情感)。接受与探究(方式)。
﹡﹡例子的选择至关重要,“一个好例子胜过一千条说教”。
﹡﹡“细节决定成败”――设问,选题,概念等细节。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com