
1、突出重点知识,引领落实“双基”-初中数学核心内容及主要思想方法是考查的重点,基础性的常规题是试题的主体。
3、《试题资料》,赣州市初中数学试题研讨小组:林望春,黄水根,郭元军,黄瑞英,马跃进、赵声洪,李 明、肖 庆等老师
2、历年《全国中考数学考试评价报告》 全国中考数学评价课题组 张远增博士等
1、江西省教研室 喻汉林老师 《起始年级学生数学学习准备状况分析》
8、学会从多角度、多层次地进行归类总结。如:①从数学思想分类;②从解题方法归类;③从知识应用上分类等;最终使所学的知识系统化、条理化、专题化、网络化。 9、经常在做题后进行一定的“反思”。数学问题解答完成之后,思考一下本题所用的基础知识,数学思想方法是什么?为什么要这样想,是否还有别的想法和解法?本题的分析方法与解法,在解其它问题时,是否也使用过? 10、无论是作业还是测验,都应把准确性放在第一位,通法通则放在第一位。而不是一味地去追求速度或技巧,这是学好数学的重要方法。
欢迎批评指正!谢谢!
2009年3月14日
参考资料:
4、熟记一些数学规律和数学小结论。能使自己平时的运算技能达到自动化或半自动化的熟练程度。教师讲解时,一定有适量的归纳总结:重要结论,常用方法,规范的步骤;而不会是杂乱无章。
2、经常对知识结构进行梳理,形成板块结构。实行“整体集装”,如表格化,使知识结构一目了然;经常对习题进行类化,由一例到一类,由一类到多类,由多类到统一;使几类问题归纳于同一知识方法。 3、记数学笔记。特别是对概念理解的不同侧面和数学规律,教师在课堂中拓展的知识交汇点,通法通则等,记录下来。还要记录:本章你觉得最有价值的思想方法或例题,以及你还存在的未解决的问题,以便今后将其补上。
当前中学数学教学中值得注意的几个问题--上海市教育科学研究院 顾泠沅 杨玉东
① 情境不是外衣,重在促进理解。实际问题经过教学加工才能进入课堂,扯得太远,反而冲淡学生学习的主题。
② 兴趣是动力,但不是所有的数学问题都是有趣的。一味地追求兴趣,重心发生偏移。信心有必要,成功必须大于挫折,但挫折不能等于零,学生一时的误解是重要的教学资源,课上得太顺,教师的教学机智无处发挥。
③ 数学教学不是习题教学。即使是习题,也要疏理每道题的作用与意义,多而无度、缺乏梯度是目前存在的突出问题。
④ 课题学习是不同于寻常知识内容的学习方式。它是一种让学生学会“做数学”的过程,不是教结论、更不是讲解难题。引导学生做数学,老师至少也要学会做数学。
⑤ 探究是高位的理解,好的探究必须讲究基础。合作学习与独立思考相辅相成,什么时候合作才有效应引起大家的重视。(“热闹的交流中缺少了数学本质的思考”这种现象还很常见.)
⑥“具象-表象-抽象”是递进关系。该抽象的时候用具象、做测量反而使思维水平下降;介于具象、抽象之间的表象(如线段图、示意图)思考是促进提升的重要手段。
⑦ 教材常有“混而不错”的处理。但“混”中常有陷阱,混错了对学生会产生误导;教参有时是一家之言,不能迷信,是参考借鉴,不是依据准绳。
★针对学生自己的数学学习情况,建议采取以下一些具体的措施:
1、不抛弃、不放弃 。九年级的数学总复习对于学生来说,总是有不同层次的提高;也可以说:对基础不是太差而又会努力的学生,通过对初中数学的梳理,知识缔结成板块或网络,思想方法提升,数学能力提高,数学整体成绩提高;可谓有“再造之功”。对各层次学生都要说:老师不抛弃任何一位,学生不能放弃了自己!
17.如图1,正方形 和正三角形
和正三角形 的边长都为1,点
的边长都为1,点 分别在线段
分别在线段 上滑动,设点
上滑动,设点 到
到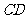 的距离为
的距离为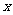 ,到
,到 的距离为
的距离为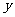 ,记
,记 为
为 (当点
(当点 分别与
分别与 重合时,记
重合时,记 ).
).
(1)当 时(如图2所示),求
时(如图2所示),求 的值(结果保留根号);
的值(结果保留根号);
(2)当 为何值时,点
为何值时,点 落在对角线
落在对角线 上?请说出你的理由,并求出此时
上?请说出你的理由,并求出此时 的值(结果保留根号);
的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
 |
 |
 |
 |
 |
 |
 |
 |
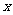 |
|
0.03 |
0 |
|
|
0.29 |
|
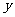 |
|
0.29 |
0.13 |
|
|
0.03 |
|
(4)若将“点 分别在线段
分别在线段 上滑动”改为“点
上滑动”改为“点 分别在正方形
分别在正方形 边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点
边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点 运动所形成的大致图形.
运动所形成的大致图形.
 (参考数据:
(参考数据: .)
.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com