
5.应用性问题:
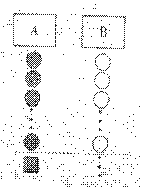 (2006年)第24题:小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a﹥8),就站到A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人。
(2006年)第24题:小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a﹥8),就站到A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人。
(1) 此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少(含a的代数式表示?)
(2) 此时,若小杰迅速从A窗口队伍转移到B窗口队伍后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其它因素)。
[评析]本题以考生所贴近的学校生活为背景,创设似真的问题情境,关注数学与生活的联系,考查学生分析问题解决问题的能力。它考查的主要知识是“数与代数”中的核心内容--用代数式表示一个量,用不等式表达生活中的不等关系和将实际问题转化为数学问题的建模能力。
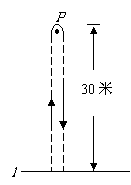 (2008年)第21题:甲、乙两同学玩“托球赛跑”游戏,商定:
(2008年)第21题:甲、乙两同学玩“托球赛跑”游戏,商定:
用球拍托着乒乓球从起跑线 起跑,绕过P点跑回到起跑线
起跑,绕过P点跑回到起跑线
(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,
用时少者胜.结果:甲同学由于心急,掉了球,浪费了6秒钟,
乙同学则顺利跑完.事后,甲同学说:“我俩所用的全部时间的
和为50秒”,乙同学说:“捡球过程不算在内时,甲的速度是我的
4. 开放性问题 :
3.网格问题:
 (2006年)第9题:请在由边为1的小正三角形组成的虚线网格中,画出一个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形。
(2006年)第9题:请在由边为1的小正三角形组成的虚线网格中,画出一个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形。
它是一道网格题,有别于以往见多的小正方形网格,而
是小正三角形网格,它很好地考查了无理数的概念,
渗透了数形结合思想,增强了学生的几何变换能力。
(2007年)第24题:在同一平面直角坐标系中有6个点:
 ,
, ,
,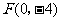 .
.
 (1)画出
(1)画出 的外接圆
的外接圆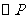 ,并指出点
,并指出点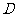 与
与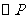 的位置关系;
的位置关系;
(2)若将直线 沿
沿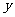 轴向上平移,
轴向上平移,
当它经过点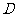 时,设此时的直线为
时,设此时的直线为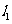 .
.
① 判断直线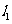 与
与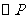 的位置关系,
的位置关系,
并说明理由;
② 再将直线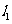 绕点
绕点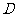 按顺时针方向旋转,
按顺时针方向旋转,
当它经过点 时,设此时的直线为
时,设此时的直线为 .
.
求直线 与
与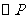 的劣弧
的劣弧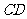 围成的图形的面积(结果保留
围成的图形的面积(结果保留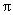 ).
).
[评析]此题将圆的内容与图形的平移、旋转通过坐标、网格(热点)这个载体有机的结合在一起,考查的知识点多、面广,有梯度,解题方法多样,是一道综合性很强的好题,充分考查了学生的基本功是否扎实。
(2008年)第8题:下列四个三角形,与右图中的三角形相似的是( )
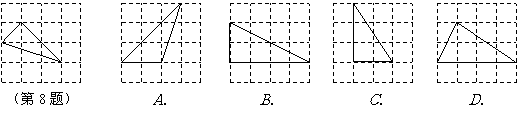

[评析]本题是一道网格题,考查了勾股定理和相似的判定。从本题可以看出网格题在考了多年后出大题已经考不出多少新意了,有可能会逐渐淡出中考大题的舞台。
21.(2007年)如图,在 中,
中,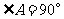 ,
, .若动点
.若动点 从点
从点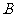 出发,沿线段
出发,沿线段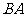 运动到点
运动到点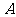 为止,运动速度为每秒2个单位长度.过点
为止,运动速度为每秒2个单位长度.过点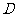 作
作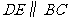 交
交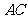 于点
于点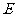 ,设动点
,设动点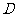 运动的时间为
运动的时间为 秒,
秒,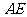 的长为
的长为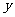 .
.
 (1)求出
(1)求出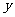 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当 为何值时,
为何值时,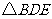 的面积
的面积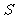 有最大值,最大值为多少?
有最大值,最大值为多少?
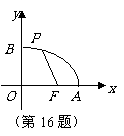 (2008年)第16题:如图,已知点
(2008年)第16题:如图,已知点 的坐标为(3,0),点
的坐标为(3,0),点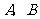 分别是某函数图象与
分别是某函数图象与 轴、
轴、 轴的交点,点
轴的交点,点 是此图象上的一动点.设点
是此图象上的一动点.设点 的横坐标为
的横坐标为 ,
,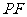 的长为
的长为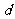 ,且
,且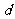 与
与 之间满足关系:
之间满足关系: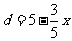 (
( ),给出以下四个结论:①
),给出以下四个结论:① ;②
;②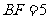 ;③
;③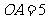 ;④
;④ .其中正确结论的序号是_ 。
.其中正确结论的序号是_ 。
[评析]这是一道非常鲜活的题目,考查学生思维的深刻性与批判性,它巧妙地把动点和函数结合在一起。本题看似难,其实很容易,只要抓住x=0和x=5这两种情况进行计算就行。
(2008年)第25题:如图1,正方形ABCD和正三角形EFG的边长都为1,点E,F分别在线段AB,AD上滑动,设点G到CD的距离为x,到BC的距离为y,记∠HEF为α(当点E,F分别与B,A重合时,记α=0°)。
(1)当α=0°时(如图2所示),求x、y的值(结果保留根号);
(2)当α为何值时,点G落在对角线AC上?请说出你的理由,并求出此时x、y的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
 |
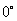 |
 |
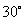 |
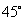 |
 |
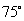 |
 |
 |
|
0.03 |
0 |
|
|
0.29 |
|
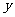 |
|
0.29 |
0.13 |
|
|
0.03 |
|
(4)若将“点E,F分别在线段AB,AD上滑动”改为“点E,F分别在正方形ABCD边上滑动”,当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出由点G运动所形成的大致图形。(参考数据: .)
.)

[评析]这是一道创新性试题,题目借运动问题考察了学生对正方形、正三角形、三角形全等、三角函数等有关知识的掌握情况。考题灵活,需要考生牢固掌握、灵活运用基础知识,通过观察、比较、分析、联想、概括、推理、归纳等一系列的探索活动,寻求隐含的条件或结论。
2、动点问题:
1、折叠问题:
(2007年) 第16题:.如图,将矩形
第16题:.如图,将矩形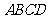 纸片沿对角线
纸片沿对角线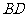 折叠,使点
折叠,使点 落在
落在 处,
处,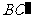 交
交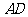 于
于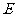 ,若
,若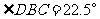 ,则在不添加任何辅助线的情况下,图中
,则在不添加任何辅助线的情况下,图中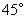 的角(虚线也视为角的边)有( )
的角(虚线也视为角的边)有( )
A.6个 B.5个 C.4个 D.3个
[评析]:本题一方面主要考查学生
的空间想象能力,另一方面还考查学
生的动手操作能力,当学生的空间想
象受到影响时,可借助动手实践,从中发现在折叠过程中不变量与变量
的特点,找到与45°角相等的所有角。 (答案B)
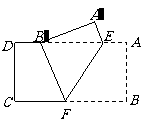 (2008年)第20题:如图,把矩形纸片
(2008年)第20题:如图,把矩形纸片 沿
沿 折叠,使点
折叠,使点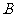 落在边
落在边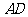 上的点
上的点 处,点
处,点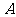 落在点
落在点 处;
处;
(1)求证: ;
;
(2)设 ,试猜想
,试猜想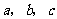 之间的
之间的
一种关系,并给予证明.
[评析]本题结合轴对称、全等、勾股定理等知识,较全面地考查了学生的动手操作能力、逻辑思维能力及猜想探索与合情推理能力。
此题有多种解法,充分发挥了一题多解的优点,能很好地体现学生的思维深度。
4、引导多思、多想、多动,全面考查能力--能力立意题仍是试题的主流。
:一组中考题赏析
3、倡导开放探究,注重实践创新--开放探索与创新性试题是考试的热点。
2、密切联系实际、强化应用意识--有鲜明的生活气息和社会价值的应用性试题,考查力度平稳。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com