
2.在下列计算中,①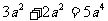 ②
②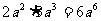 ③
③
④ 正确的有( )个。
正确的有( )个。
A、1 B、2 C、3 D、4
例4:讨论探索:(1)已知xm=64.xn=8,求xm-n (2)已知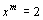 ,
,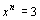 ,求
,求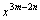
[本课小结]:
运用同底数幂的除法性质时应注意以下问题:
(1)运用法则的关键是看底数是否相同,而指数相减的是指被除式的指数减去除式的指数;
(2)因为零不能作除数,所以底数a≠0,这是此性质成立的前提条件;
(3)注意指数“1”的情况,如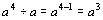 ,不能把
,不能把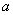 的指数当做0;
的指数当做0;
(4)多个同底数幂相除时,应按顺序计算.
[布置作业]:1、课本第4页 习题1。 2、同步练习册第1-2页。
例1 计算:
(1) a8÷a3; (2)(-a)10÷(-a) 3; (3)(2a)7÷(2a)4; (4)x6÷x
例2 计算:(1)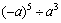 (2)(-x)6 ÷x2 (3)(a+b)4÷(a+b)2
(2)(-x)6 ÷x2 (3)(a+b)4÷(a+b)2
例3 计算: (-a2)4÷(a3)2×a4
例4 计算:(1)273×92÷312
(2)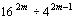
说明 底数不同的情况下不能运用同底数幂的除法法则计算.
练习1:计算: x8÷x4 = , b5÷b5 = 6y3÷y3 = (-x)4÷(-x) =
(ab)6÷(ab)2= , yn+2÷yn = , (m3)4 ÷(m2)3 = ,
252÷52 = , y9 ÷(y7 ÷y3) =
练习2:选择题
1. 下面运算正确的是( )
A.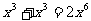 B.
B.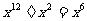 C.
C.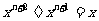 D.
D.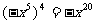
4、利用除法的意义来说明这个法则的道理。(让学生仿照问题3的解决过程,讲清道理,并请几位同学业回答问题,教师加以评析)
因为除法是乘法的逆运算,am÷an=am-n实际上是要求一个式子( ),使 an·( )= am
而由同底数幂的乘法法则,可知 an·am-n=an+(m-n) =am,
所以要求的式( ),即商为am-n,从而有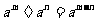 .
.
3、概 括
由上面的计算,我们发现:
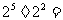 23=
;
23=
; 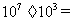 104= ;
104= ;  .
.
在学生讨论、计算的基础上,教师可提问,你能发现什么?
由学生回答,教师板书,发现
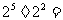 23=25-2
23=25-2
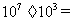 104=107-3;
104=107-3;
 a4=a7-3.
a4=a7-3.
你能根据除法的意义来说明这些运算结果是怎么得到的吗?
分组讨论:各组选出一个代表来回答问题,师生达成共知识,除法与乘法是逆运算,所以除法的问题实际上“已知乘积和一个乘数,去求另一个乘数”的问题,于是上面的问题可以转化为乘法问题加以解决。即
( )× =
=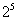 (
)×
(
)×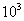 =
=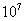 ( )×
( )×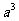 =
=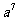
一般地,设m、n为正整数,m>n,a≠0,有
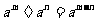 .
.
这就是说,同底数幂相除,底数不变,指数相减。
2、试一试
用你熟悉的方法计算:
(1)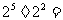 ___________;(2)
___________;(2)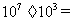 ___________;(3)
___________;(3) ___________(a≠0)
___________(a≠0)
1、 们知道同底数幂的乘法法则: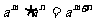 ,那么同底数幂怎么相除呢?
,那么同底数幂怎么相除呢?
现要装配30台机器,在装配好6台后,采用了新的技术,每天的工作效率提高了一倍,结果共用了3天完成任务。如果设原来每天能装配x台机器,那么不难列出方程:
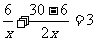
这个方程左边的式子已不再是整式,这就涉及到分式与分式方程的问题.
(一)较好的方面
1、运算准确性更高了.T17、T18的得分率均在60%以上,T9 、T13 的得分率均为84%,说明学生的运算能力提高了,仅仅因为运算造成失分的象现大大减少了.
2、基本功更扎实了.第一大题的得分率为78.7%、第二大题的得分率为69.3%、第三大题的得分率分为61.7%,说明学生具有较为扎实的基础知识,从而保证了低分率有所下降,平均分再度上升.
3、解题方法更多样化了.T20多数学生能抓住题中“翻折”实际上对应于“点B点B′点关于EF对称”,从而得到多种不同解题方法;T21有些学生能从不同的角度来审视问题,解法有独特之处,甚至不用方程用算式就解出来了,还有的学生不受条件“30米”的牵制,将来回的路程视为“整体1”,思维这活跃、思路之敏捷、手段之高明,这正是课改给我们的数学教学带来的可喜变化;T22学生根据圆中常规连辅助线(连半径、过圆心弦的垂线等)的方法,或直接利用圆周角与圆心角的关系,或利用等腰三角形三线合一性质、圆周角与圆心角的关系,或利用圆周角定理,把α与β放在同一个直角三角形形中,都能顺利得到α+β=90°,这真是“条条大路通过罗马”,不仅说明命题设计的问题有很大的思考空间,同时也反映出学生的思维更灵活了,视野更开阔了,方法更多样化了.
4、探究能力更强了.尽管试题中出现了三道猜想题(T20 、T22 、T25)和两道开放探究题(T23 、T24),都是中难度试题,但这并没有影响学生的情绪和成绩,相反,还反映了学生的探究能力有了很大的提高.如T25的第(2)问,学生先从一些特殊角入手,大胆猜想当α=45°时,对应的等腰Rt△EAF、等边△EFG、正方形ABCD都是关于对角线AC成轴对称图形,从而进一步给出合理的解释;T23 和T24得出了很多正确结论.
5、读图、识图、析图能力更强了.全卷共有16道题配有图形,学生必须快速、准确的从图中获取有价值的信息,来分析、解决问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com