
2.选用课时作业设计.
第一课时作业设计
1.教材P8复习巩固1、综合应用5.
2.要使二次根式在实数范围内有意义,必须满足被开方数是非负数.
本节课要掌握:
1.形如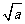 (a≥0)的式子叫做二次根式,“
(a≥0)的式子叫做二次根式,“ ”称为二次根号.
”称为二次根号.
例3.当x是多少时, +
+ 在实数范围内有意义?
在实数范围内有意义?
分析:要使 +
+ 在实数范围内有意义,必须同时满足
在实数范围内有意义,必须同时满足 中的≥0和
中的≥0和 中的x+1≠0.
中的x+1≠0.
解:依题意,得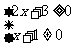
由①得:x≥-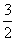
由②得:x≠-1
当x≥-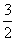 且x≠-1时,
且x≠-1时, +
+ 在实数范围内有意义.
在实数范围内有意义.
例4(1)已知y=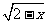 +
+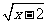 +5,求
+5,求 的值.(答案:2)
的值.(答案:2)
(2)若 +
+ =0,求a2004+b2004的值.(答案:
=0,求a2004+b2004的值.(答案: )
)
教材P练习1、2、3.
3.当a<0,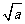 有意义吗?
有意义吗?
老师点评:(略)
例1.下列式子,哪些是二次根式,哪些不是二次根式: 、
、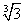 、
、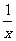 、
、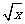 (x>0)、
(x>0)、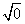 、
、 、-
、- 、
、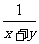 、
、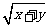 (x≥0,y≥0).
(x≥0,y≥0).
分析:二次根式应满足两个条件:第一,有二次根号“ ”;第二,被开方数是正数或0.
”;第二,被开方数是正数或0.
解:二次根式有: 、
、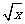 (x>0)、
(x>0)、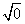 、-
、- 、
、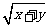 (x≥0,y≥0);不是二次根式的有:
(x≥0,y≥0);不是二次根式的有: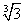 、
、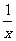 、
、 、
、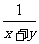 .
.
例2.当x是多少时, 在实数范围内有意义?
在实数范围内有意义?
分析:由二次根式的定义可知,被开方数一定要大于或等于0,所以3x-1≥0, 才能有意义.
才能有意义.
解:由3x-1≥0,得:x≥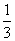
当x≥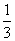 时,
时, 在实数范围内有意义.
在实数范围内有意义.
2.0的算术平方根是多少?
很明显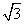 、
、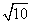 、
、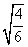 ,都是一些正数的算术平方根.像这样一些正数的算术平方根的式子,我们就把它称二次根式.因此,一般地,我们把形如
,都是一些正数的算术平方根.像这样一些正数的算术平方根的式子,我们就把它称二次根式.因此,一般地,我们把形如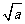 (a≥0)的式子叫做二次根式,“
(a≥0)的式子叫做二次根式,“ ”称为二次根号.
”称为二次根号.
(学生活动)议一议:
1.-1有算术平方根吗?
(学生活动)请同学们独立完成下列三个问题:
问题1:已知反比例函数y=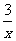 ,那么它的图象在第一象限横、纵坐标相等的点的坐标是___________.
,那么它的图象在第一象限横、纵坐标相等的点的坐标是___________.
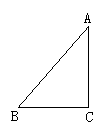
问题2:如图,在直角三角形ABC中,AC=3,BC=1,∠C=90°,那么AB边的长是__________.
问题3:甲射击6次,各次击中的环数如下:8、7、9、9、7、8,那么甲这次射击的方差是S2,那么S=_________.
老师点评:
问题1:横、纵坐标相等,即x=y,所以x2=3.因为点在第一象限,所以x=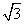 ,所以所求点的坐标(
,所以所求点的坐标(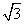 ,
,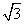 ).
).
问题2:由勾股定理得AB=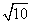
问题3:由方差的概念得S= 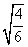 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com