
6、某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表(单位:分)
|
|
A |
B |
C |
D |
E |
|
甲 |
90 |
92 |
94 |
95 |
88 |
|
乙 |
89 |
86 |
87 |
94 |
91 |
表2 民主测评票统计表(单位:张)
|
|
“好”票数 |
“较好”票数 |
“一般”票数 |
|
甲 |
40 |
7 |
3 |
|
乙 |
42 |
4 |
4 |
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
第4课时 加权平均数的应用
教学过程
5、小颖家去年的饮食支出为3600元,教育支出为1200元,其他支出为7200元,小颖家今年的这三项支出依次比去年增长了9%,30%,6%,小颖家今年的总支出与去相比增长的百分数是多少?
4、某班有40名学生,其中14岁的有10人,15岁的有20人,16岁的有10人,这个班学生的平均年龄为_____________岁.
3、某校举行运动会,按年级设奖,第一名得5分,第二名得3分,第三名得2分,第四名得1分,某班派8名同学参加比赛,共得2个第一,1个第三,4个第四,则该班8名同学的平均得分为______________.
2、某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为( )
A、35 B、3 C、0.5 D、-3
黑板分为左、中、右三部分,中间与右边用于教师板书课本例题等,写满后擦去更新.左边用于板书以下内容:
扇形统计图能形象地表达各分量在总量中所占份额大小.
扇形图的作法:1、计算百分比;2、计算圆心角;3、画扇形图.
第3课时作业优化设计
1、有m个数的平均值是x,n个数的平均值是y,则这m+n个数的平均值是( )
A、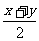 B、
B、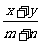 C、
C、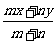 D、
D、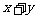
本节课要让学生通过实际问题理解权重的概念(不要求学生掌握它的定义,能理解会用就行)并能计算加权平均数.
布置作业
1、课本第138页习题21.1第6题.
课本第133页练习
(二)例题讲解
教师提出问题:某公司对应聘者A、B、C、D进行面试,并按三个方面给应聘者打分,最后打分结果如下表所示,如果你是人事主管,会录用哪一个应聘者?
四位应聘者的面试成绩
|
|
满分 |
A |
B |
C |
D |
|
专业知识 |
20 |
14 |
18 |
17 |
16 |
|
工作经验 |
20 |
18 |
16 |
14 |
16 |
|
仪表形象 |
20 |
12 |
11 |
14 |
14 |
教师提出各种不同意见让学生分析:甲同学说:看谁的总分高就录用谁,通过计算可以发现D的总分最高,应被录用.这时乙同学说:我有不同意见,三个方面满分都是20分,但按理这三个方面的重要性应该有所不同,比如专业知识就应该比仪表形象更重要.所以不能像甲同学所说的那样平均.
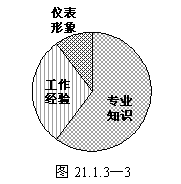
教师指出,显然乙同学的意见更为合理.教师再提出:假设上述三个方面的重要性之比为6∶3∶1(如图21.1.3-3),那么应该录用谁呢?
教师给出A应聘者得分的计算方法:(见课本第135页)
教师要求学生模仿上述计算方法算出另三位应聘者的最后得分.然后从计算结果来确定谁应被录用.
学生计算完后教师给出答案.
教师提出以下问题让学生计算:如果这三个方面的重要性之比为10∶7∶3,此时哪个方面的权重最大?哪一位应被录用呢?
学生计算后会发现,4个人的分数全改变了,得分最高的人也改变了.通过这一题要让学生领会,权重的选择既要符合客观实际,又要带有人为的因素.
(一)加权概念的引入
教师讲解;一般来说,由于各个指标在总结果中占有不同的重要性,因而会被赋予不同的权重,上例中的40%与60%就是平时成绩与考试成绩在学期总评成绩中的权重,最后计算得到的学期总评成绩82分就是上述两个成绩的加权平均数.
教师要求学生模仿上题计算下面问题:小青在初一年级第二学期的数学成绩分别为:第1次测验得89分,第二次测验得78分,第3次测验得85分,期中考试得90分,期末考试得87分.如果按照图21.1.3-2所显示的平时、期中、期末成绩的权重,那么小青该学期的总评成绩应该为多少分?
 学生计算后教师给出答案.设置此题的目的主要是让学生熟悉按权重计算平均值的方法.
学生计算后教师给出答案.设置此题的目的主要是让学生熟悉按权重计算平均值的方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com