
2、某校把学生的笔试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀,甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
|
|
纸笔测试 |
实践能力 |
成长记录 |
|
甲 |
90 |
83 |
95 |
|
乙 |
88 |
90 |
95 |
|
丙 |
90 |
88 |
90 |
A、甲 B、乙、丙 C、甲、乙 D、甲、丙
1、下表中,若平均数为2,则x等于( )
|
分数 |
0 |
1 |
2 |
3 |
4 |
|
学生人数 |
x |
5 |
6 |
3 |
2 |
A、0 B、1 C、2 D、3
2、选用课时作业优化设计.
第4课时作业优化设计
1、课本第138页习题21.1第5、7题.
要求学生在实际应用中懂得加权平均的应用场合.
课本第134页练习.
(二)例题讲解
教师提出问题:为推选一名同学参加学校演讲比赛,班里组织了一次选拔赛,由教师组成评委,对甲、乙、丙三名候选人分别从演讲内容、语言表达能力和感染力三方面打分,评委打分的结果如下表:
|
测试项目 |
演讲内容 |
语言表达能力 |
感染力 |
|
甲的成绩/分 |
9.0 |
8.6 |
8.0 |
|
乙的成绩/分 |
8.0 |
9.2 |
8.2 |
|
丙的成绩/分 |
9.4 |
8.8 |
7.5 |
1、如果按三项得分的算术平均数确定优胜者,谁是优胜者?
2、如果三项得分分别按25%,35%,40%的比例计算总成绩,谁是优胜者?
3、哪一种计算方法比较合理,你认为要选哪一个学生去参加比赛?
学生解答后,教师给出解题步骤:
(1)甲、乙、丙按三项得分的算术平均数分别是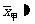 8.53(分),
8.53(分), 8.47(分),
8.47(分),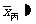 8.57(分).比较算术平均数,丙是优胜者.
8.57(分).比较算术平均数,丙是优胜者.
(2)甲、乙、丙按三项得分的加权平均数分别是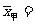 8.46(分),
8.46(分),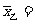 8.5(分),
8.5(分),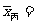 8.43(分).比较加权平均数,乙是优胜者.
8.43(分).比较加权平均数,乙是优胜者.
(3)第(2)种算法比较合理,应选乙参加比赛.
(一)课本例4讲解
教师提出问题:一架电梯的最大载重是1000千克,现有13位“重量级”的乘客要搭乘电梯,已知其中11位先生的平均体重是80千克,2位女士的平均体重是70千克,请问他们能否一起安全地搭乘这架电梯?他们的平均体重是多少千克?
教师要求学生自己解答上述问题.学生做完后教师给出正确解答:(见课本第134页)
教师强调:这是一个已知两个平均数再求总平均数的问题,解这类问题一般不能采取“相加除以2”的平均化策略.因为两个方面的权重不相等.
3.50×25%+4×75%=3.85元/千克
通过本题复习旧课,加深学生对加权平均的认识.
教师讲解:上节课我们介绍了加权平均的概念,初步会计算一个量在不同取值时的加权平均.这节课我们将应用加权平均概念解决实际问题.
首先我们来思考下列问题来加深我们对权重的认识:商店里有两种苹果,一种单价是3.50元/千克,另一种单价为4元/千克.如妈妈各买了2千克,那么妈妈所买苹果的平均价格为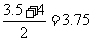 (元/千克),这种算法对吗?为什么?
(元/千克),这种算法对吗?为什么?
如果妈妈买了单价为3.50元/千克的苹果1千克,单价为4元/千克的苹果3千克,那么这种算法对吗?为什么?
学生回答后教师提出:如果不同价格的苹果买的数量一样,也就是权重一样,那么采用上述方法取平均数是合理的.如果按加权计算,每种苹果价格的权重都为50%,其价格的平均数为
3.50×50%+4×50%=(3.50+4)÷2=3.75元/千克
上面的计算结果与问题中所采用的计算结果是一样的.
如果不同价格的苹果买的斤数不一样,就不能用上述计算方法.因为这时单价为3.50元/千克的苹果的权重为25%,单价为4元/千克的苹果的权重为75%,加权平均的计算方法是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com