
1.(-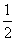 +
+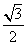 )2的计算结果(用最简根式表示)是________.
)2的计算结果(用最简根式表示)是________.
2.计算(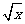 +
+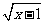 )(
)(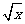 -
-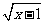 )的值是( ).
)的值是( ).
A.2 B.3 C.4 D.1
1.(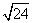 -3
-3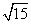 +2
+2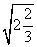 )×
)× 的值是( ).
的值是( ).
A.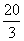
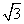 -3
-3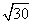 B.3
B.3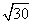 -
-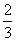
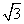 C.2
C.2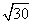 -
-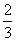
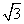 D.
D.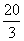
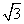 -
-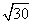
2.选用课时作业设计.
作业设计
1.教材P21 习题21.3 1、8、9.
本节课应掌握二次根式的乘、除、乘方等运算.
例3.已知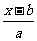 =2-
=2-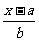 ,其中a、b是实数,且a+b≠0,
,其中a、b是实数,且a+b≠0,
化简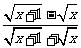 +
+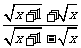 ,并求值.
,并求值.
分析:由于(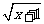 +
+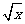 )(
)(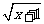 -
-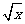 )=1,因此对代数式的化简,可先将分母有理化,再通过解含有字母系数的一元一次方程得到x的值,代入化简得结果即可.
)=1,因此对代数式的化简,可先将分母有理化,再通过解含有字母系数的一元一次方程得到x的值,代入化简得结果即可.
解:原式=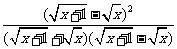 +
+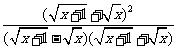
=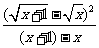 +
+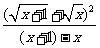 =(x+1)+x-2
=(x+1)+x-2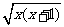 +x+2
+x+2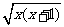
=4x+2
∵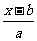 =2-
=2-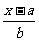 ∴b(x-b)=2ab-a(x-a)∴bx-b2=2ab-ax+a2
∴b(x-b)=2ab-a(x-a)∴bx-b2=2ab-ax+a2
∴(a+b)x=a2+2ab+b2 ∴(a+b)x=(a+b)2
∵a+b≠0∴x=a+b ∴原式=4x+2=4(a+b)+2
课本P20练习1、2.
如果把上面的x、y、z改写成二次根式呢?以上的运算规律是否仍成立呢?仍成立.
整式运算中的x、y、z是一种字母,它的意义十分广泛,可以代表所有一切,当然也可以代表二次根式,所以,整式中的运算规律也适用于二次根式.
例1.计算:
(1)(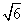 +
+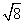 )×
)×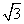 (2)(4
(2)(4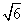 -3
-3 )÷2
)÷2
分析:刚才已经分析,二次根式仍然满足整式的运算规律,所以直接可用整式的运算规律.
解:(1)(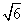 +
+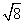 )×
)×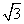 =
=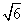 ×
×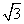 +
+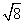 ×
×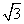 =
=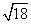 +
+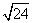 =3
=3 +2
+2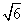
解:(4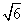 -3
-3 )÷2
)÷2 =4
=4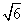 ÷2
÷2 -3
-3 ÷2
÷2 =2
=2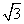 -
-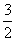
例2.计算
(1)(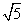 +6)(3-
+6)(3-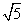 ) (2)(
) (2)(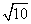 +
+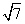 )(
)(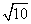 -
-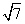 )
)
分析:二次根式的多项式乘以多项式运算在乘法公式运算中仍然成立.
解:(1)(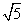 +6)(3-
+6)(3-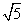 )=3
)=3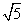 -(
-(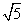 )2+18-6
)2+18-6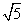 =13-3
=13-3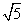
(2)(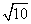 +
+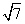 )(
)(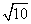 -
-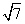 )=(
)=(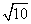 )2-(
)2-(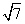 )2
=10-7=3
)2
=10-7=3
2.计算
(1)(2x+3y)(2x-3y) (2)(2x+1)2+(2x-1)2
老师点评:这些内容是对八年级上册整式运算的再现.它主要有(1)单项式×单项式;(2)单项式×多项式;(3)多项式÷单项式;(4)完全平方公式;(5)平方差公式的运用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com