
知识与技能
1、理解正方形的概念,了解正方形与平行四边形、菱形、矩形的关系.
4.其它材料:如果n是任意正整数,那么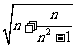 =n
=n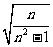
理由: =
=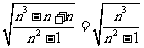 =n
=n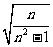
练习:填空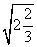 =_______;
=_______;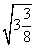 =________;
=________;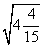 =_______.
=_______.
3.分母有理化是指把分母中的根号化去,通常在分子、分母上同乘以一个二次根式,达到化去分母中的根号的目的.
练习:把下列各式的分母有理化
(1)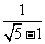 ; (2)
; (2)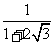 ; (3)
; (3)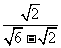 ; (4)
; (4) .
.
2.互为有理化因式:互为有理化因式是指两个二次根式的乘积可以运用平方差公式(a+b)(a-b)=a2-b2,同时它们的积是有理数,不含有二次根式:如x+1-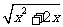 与x+1+
与x+1+ 就是互为有理化因式;
就是互为有理化因式;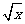 与
与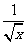 也是互为有理化因式.
也是互为有理化因式.
练习: +
+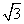 的有理化因式是________;
的有理化因式是________;
x- 的有理化因式是_________. -
的有理化因式是_________. -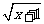 -
-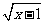 的有理化因式是_______.
的有理化因式是_______.
1.同类二次根式:几个二次根式化成最简二次根式后,它们的被开方数相同,这些二次根式就称为同类二次根式,就是本书中所讲的被开方数相同的二次根式.
练习:下列各组二次根式中,是同类二次根式的是( ).
A.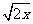 与
与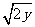 B.
B.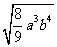 与
与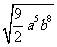 C.
C.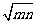 与
与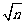 D.
D.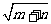 与
与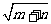
2.当x=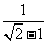 时,求
时,求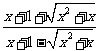 +
+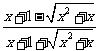 的值.(结果用最简二次根式表示)
的值.(结果用最简二次根式表示)
课外知识
1.化简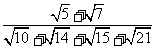
4.已知a=3+2 ,b=3-2
,b=3-2 ,则a2b-ab2=_________.
,则a2b-ab2=_________.
3.若x= -1,则x2+2x+1=________.
-1,则x2+2x+1=________.
2.(1-2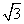 )(1+2
)(1+2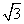 )-(2
)-(2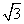 -1)2的计算结果(用最简二次根式表示)是_______.
-1)2的计算结果(用最简二次根式表示)是_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com