
(二)合作交流,探究新知
Ⅰ、正方形的判定
[探究] 操作1 你能否利用手中的矩形白纸裁出一个正方形呢?并请你把刚才所做的实验用图形表示出来.然后与邻位同学交流一下,你能说说矩形与正方形的关系吗?
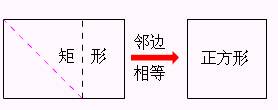
正方形的判定2 有一组邻边相等的矩形是正方形.
操作2 你能否利用手中的可以活动的菱形模型变成一个正方形吗?如何变?请演示并画出图形.
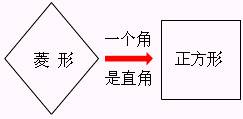
正方形的判定 3 有一个角是直角的菱形是正方形.
[练习]:判断满足下列条件的四边形是否是正方形,并说明理由:
1、对角线互相垂直且相等的平行四边形.
2、对角线互相垂直的矩形.
3、对角线相等的菱形.
4、对角线互相垂直平分且相等的四边形.
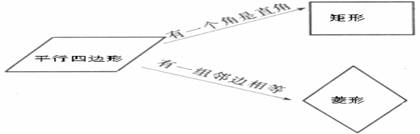
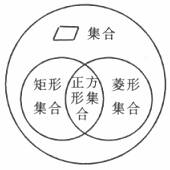 [归纳]正方形与矩形、菱形、平行四边形间的关系如图.
[归纳]正方形与矩形、菱形、平行四边形间的关系如图.
Ⅱ、正方形的性质
[交流]根据上述关系可知,正方形既是特殊的矩 形、又是特殊的菱形,更是的特殊的平行四边形,你能说出正方形的性质吗?
[点拨]从边、角、对角线等方面考虑.
边:对边平行、四条边都相等
角:四个角都是直角
对角线:对角线相等,互相垂直平分,每条对角线平分一组对角
[归纳]性质1:正方形的四条边都相等,四个角都是直角.
性质2:正方形的两条对角线相等且互相垂直平分,每条对角线平分一组对角.
[问题]正方形是中心对称图形吗?如是,对称中心在哪里?
正方形是轴对称图形吗?如是,它有几条对称轴?
对称性:正方形是中心对称图形;同时还是轴对称图形,它有四条对称轴(两条对角线,两组对边的中垂线.),对称轴通过对称中心.如图
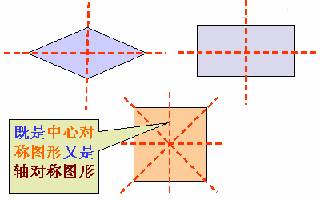
正方形具有平行四边形、矩形、菱形的一切性质.
(一)创设情境,导入新知
Ⅰ、导言 我们已学习了矩形、菱形,它们都是特殊的平行四边形.
Ⅱ、抢答 1、让学生根据所准备的模型分别叙述矩形、菱形的定义及其性质.
2、平行四边形,矩形,菱形的内在联系.
Ⅲ、引人 演示模型
[问题]根据小学学过的正方形的知识,你能说出正方形的意义吗?
四条边都相等,四个角都是直角的四边形是正方形.
[定义]有一组邻边相等,有一个角是直角的平行四边形叫做正方形.
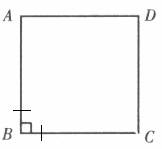 如图正方形ABCD.
如图正方形ABCD.
正方形是在什么前提下定义的?
(平行四边形)
[思考]如果四边形ABCD已经是一个矩形(或者菱形), 那么再加上什么条件就可以变为正方形?
教学方法:探究法
教学手段:多媒体辅助教学 几何模型
教学重点:正方形的定义和性质
教学难点:四边形成为正方形的条件
教学关键:正方形与平行四边形、菱形、矩形的关系
2、通过理解特殊的平行四边形之间的内在联系,培养学生辩证观点.
1、经历探索正方形有关性质和四边形成为正方形的条件过程,培养学生动手操作的能力、主动探究的习惯和合作交流的意识.
2、通过四边形从属关系的教学,渗透集合思想.
情感态度与价值观
1、通过观察、实验、归纳、类比获得数学猜想,发展学生的合情推理能力,进一步提高学生逻辑思维能力.
3、能运用正方形的性质解决有关计算和证明问题.
过程与方法
2、掌握正方形的有关性质和判定方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com