(二)合作交流，探究新知

Ⅰ、正方形的判定

　　 　　[探究] 操作1 　你能否利用手中的矩形白纸裁出一个正方形呢？并请你把刚才所做的实验用图形表示出来．然后与邻位同学交流一下，你能说说矩形与正方形的关系吗？

正方形的判定2　 有一组邻边相等的矩形是正方形．

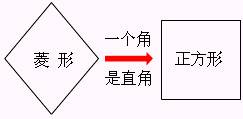
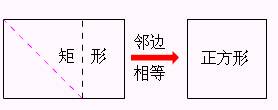操作2　 你能否利用手中的可以活动的菱形模型变成一个正方形吗？如何变？请演示并画出图形．

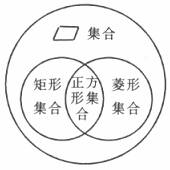正方形的判定 3　 有一个角是直角的菱形是正方形．

[练习] 课本P₇₇练习1、

[归纳]正方形与矩形、菱形、平行四边形间的关系　　　 　　　　　　　　如图．

Ⅱ、正方形的性质

[交流]根据上述关系可知，正方形既是特殊的矩　　 　　　　　　　　　形、又是特殊的菱形，更是的特殊的平行四边形，你能说出正方形的性质吗？

[点拨]从边、角、对角线等方面考虑．

　[归纳]性质1：正方形的四条边都相等，四个角都是直角．

性质2：正方形的两条对角线相等且互相垂直平分，每条对角线平分一组对角．

[问题]正方形是中心对称图形吗？ 是轴对称图形吗？

　　 对称性：正方形是中心对称图形；同时还是轴对称图形，它有四条对称轴(两条对角线，两组对边的中垂线)，对称轴通过对称中心．

　　 　　正方形具有平行四边形、矩形、菱形的一切性质．

(一)创设情境，导入新知

　Ⅰ、导言　 我们已学习了矩形、菱形，它们都是特殊的平行四边形．

　Ⅱ、抢答　 1、让学生根据所准备的模型分别叙述矩形、菱形的定义及其性质．

2、平行四边形，矩形，菱形的内在联系．

Ⅲ、引人 　演示模型

[问题]根据小学学过的正方形的知识，你能说出正方形的意义吗？

[定义]有一组邻边相等，有一个角是直角的平行四边形叫做正方形．

正方形是在什么前提下定义的？

[思考]如果四边形ABCD已经是一个矩形(或者菱形)，那么再加上什么条件就可以变为正方形？

2、学法指导

这节几何课是在八年级5班上的一节课。该班学生基础一般，但上课很活跃，有很强的表现欲，通过前一学期的培养，具有一定的独立思考和探究的能力。所以在本节课的教学过程中，设计了让学生演示模型以展示自己的劳动成果，组织语言培养说理能力，进一步提高学生逻辑思维能力．

本节课重点以培养学生探索精神和分析归纳总结能力为出发点，着重指导学生动手、观察、思考、分析、总结得出结论。在小组讨论中通过互相学习、讨论交流，让学生体验合作学习的乐趣，享受成功的喜悦。

1、教法分析

针对本节课的特点，采用“创设情境-合作交流-应用迁移-整理反思”为主线的探究式教学方法。

通过演示模型，回顾小学学过的正方形的知识，导出正方形的概念；然后由学生动手折纸(矩形-正方形)，演示菱形、平行四边形的自制教具，以矩形、菱形、平行四边形为基础，引导学生从这三条思路进行探索一个四边形成为正方形的条件；由正方形与平行四边形、菱形、矩形的关系，通过讨论交流、归纳总结出正方形性质定理(边、角、对角线、对称性)；最后以课堂练习、例题讲解、问题研讨，加深了对正方形定义、性质的理解，巩固了对判定的的掌握。

整个教学过程中教师通过演示、提问、观察、点拨，充分调动学生非智力因素，动手实践、合作交流，让学生在老师的引导下自始至终处于一种积极思维、主动学习的学习状态。而教师在其中当好课堂教学的组织者、引路人。

3、教学重点、难点

学生在小学学过正方形，他们知道正方形的四个角都是直角，四条边相等，正方形的面积等于它的边长的平方。现在的教学是加深学生的理论知识，拓宽他们的知识面。本节课虽然是学习正方形的性质和判定，实际上应起到对平行四边形、菱形、矩形性质的复习、归纳和总结的作用。所以正方形的定义和性质是本章教学的重点。怎样判定一个四边形是正方形，这是本章教学的一个难点。因为没有具体的判定定理，学生不知道人哪里着手来判定一个四边形是正方形，具体证明时，常出现步骤混乱，或多用或少条件的现象，解决这个难点的关键是加强正方形概念的教学，讲清正方形与平行四边形、菱形、矩形的关系。

依据课程标准，在把握教材的基础上，确立如下的教学重点、难点：

教学重点：正方形的定义和性质

教学难点：四边形成为正方形的条件

教学关键：正方形与平行四边形、菱形、矩形的关系

2、教育教学目标

根据上述教材分析，考虑到学生已有的认知结构心理特征，制定如下教学目标：

⑴知识与技能

①、理解正方形的概念，了解正方形与平行四边形、菱形、矩形的关系．

②、掌握正方形的有关性质和判定方法．

③、能运用正方形的性质解决有关计算和证明问题．

⑵过程与方法

①、通过观察、实验、归纳、类比获得数学猜想，发展学生的合情推理能力，进一步提高学生逻辑思维能力．

②、通过四边形从属关系的教学，渗透集合思想．

⑶情感态度与价值观

①、经历探索正方形有关性质和四边形成为正方形的条件过程，培养学生动手操作的能力、主动探究的习惯和合作交流的意识．

②、通过理解特殊的平行四边形之间的内在联系，培养学生辩证观点．

1、教材地位和作用

《正方形》这节课是新课标沪版数学教材八年级下册第21章第三节的内容。纵观整个初中平面几何教材，《正方形》是在学生掌握了平行线、三角形、平行四边形、矩形、菱形等有关知识，并且具备有初步的观察、操作等活动经验的基础上出现的。本节教材首先从平行四边形出发，给出正方形的定义，然后由正方形的定义导出正方形与菱形、矩形的关系，接着出了正方形的性质；通过设置“思考”栏目，探索四边形成为正方形的条件，最后由例题具体说明正方形的判定方法。这一节课既是前面所学知识的延续，又是对平行四边形、菱形、矩形进行综合的不可缺少的重要环节。

(四)整理反思、评价体验

通过这节课的学习，我们有哪些收获？

引导学生从知识内容、数学思想方法两方面进行小结．

正方形的定义、判定方法和性质．

1、正方形与 矩形，菱形，平行四边形的关系．

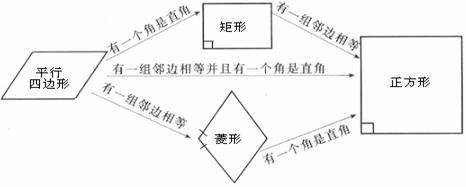
2、正方形的性质:

正方形具有矩形和菱形的一切性质

a 边: 　四条边都相等　

　　　　　　　　　　　　　　　 (性质1)

　b 角:　　 四个角都是直角

c 对角线:相等．互相垂直平分,

　　 每条对角线平分一组对角 (性质2)

正方形的性质与平行四边形、矩形、菱形的性质可比较如下：

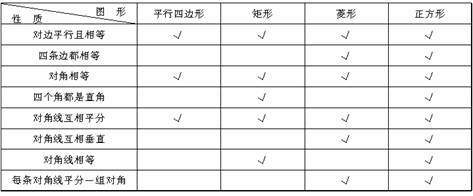
(师生同完成，凡是图形所具有的性质，在表中相应的空格中填上“√”，没有的性质不要填写)

由表中可知：因为正方形既是特殊的平行四边形，又是特殊的矩形，特殊的菱形，所以正方形具有平行四边形、矩形、菱形的一切性质，又具有自身的特殊性质．

(三)应用迁移，巩固提高

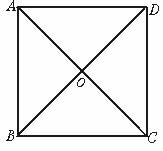
Ⅰ、[问题] 如图，四边形ABCD是正方形，两条对角线相交于点O．

(1)一条对角线把它分成_______个全等的________ 三角形；

(2)两条对角线把它分成_______个全等的________三角形；

图中一共有________个等腰直角三角形；

(3)∠AOB＝_____度，∠OAB＝_____度．

(4)AB: AO: AC=________．

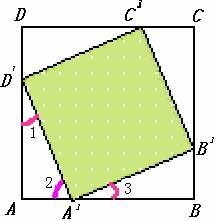
Ⅱ、例6、如图，点A＇、B＇、C＇、D＇分别是正方形ABCD　　　　四条边上的点，并且AA＇=BB＇=CC＇=DD＇．

求证：四边形A＇B＇C＇D＇是正方形．

证明： 因为四边形ABCD是正方形，所以

　　　 　AB＝BC＝CD＝DA．

又 ∵AA＇=BB＇=CC＇=DD＇，

∴D＇A＝A＇B＝B＇C＝C＇D．

　　 ∵∠A＝∠B＝∠C＝∠D＝90⁰，

∴△AA＇D＇≌△BB＇A＇

≌△CC＇B＇≌△DD＇C＇，(SAS)

∴A＇B＇＝B＇C＇＝C＇D＇＝D＇A＇，

　 　　即四边形A＇B＇C＇D＇是菱形．

又 ∵∠1＝∠3，∠1+∠2＝90⁰，

∴∠2+∠3＝90⁰，∴∠D＇A＇B＇＝90⁰．

所以四边形A＇B＇C＇D＇是正方形．

Ⅲ、[论证]课本第77页练习3：

如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形．求证：△ABF≌△DAE．

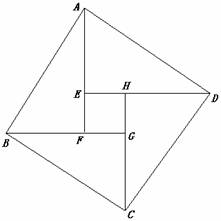
证明：∵四边形EFGH是正方形，

∴∠AFB＝∠DEA＝90⁰，　 且 ∠ABF+∠BAF＝90⁰，

又∵∠BAF+∠DAE＝90⁰， ∴∠ABF＝∠DAE．

又∵AB＝DA，　 ∴△ABF≌△DAE(AAS)．