2．方程2x²=3(x-6)化为一般形式后二次项系数、一次项系数和常数项分别为( )．

　　　 A．2，3，-6　　 B．2，-3，18　　 C．2，-3，6　　 D．2，3，6

1．在下列方程中，一元二次方程的个数是(　 )．

　　　 ①3x²+7=0　　 ②ax²+bx+c=0　　 ③(x-2)(x+5)=x²-1　　 ④3x²-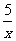=0

　　　 A．1个　　 B．2个　　 C．3个　　 D．4个

　 　例3．求证：关于x的方程(m²-8m+17)x²+2mx+1=0，不论m取何值，该方程都是一元二次方程．

　　 作业设计

　　 教材P₃₂　 练习1、2

　　 (1)上面三个方程整理后含有几个未知数？

　　 (2)按照整式中的多项式的规定，它们最高次数是几次？

　　 (3)有等号吗？或与以前多项式一样只有式子？

　 说明(1)都只含一个未知数x；(2)它们的最高次数都是2次的；(3)都有等号，是方程．

　　 因此，像这样的方程两边都是整式，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程，叫做一元二次方程．

　　 一般地，任何一个关于x的一元二次方程，经过整理，都能化成如下形式ax²+bx+c=0(a≠0)．这种形式叫做一元二次方程的一般形式．

　　 一个一元二次方程经过整理化成ax²+bx+c=0(a≠0)后，其中ax²是二次项，a是二次项系数；bx是一次项，b是一次项系数；c是常数项．

　 　例1．将方程(8-2x)(5-2x)=18化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项．

　 　例2．(学生活动：请二至三位同学上台演练)　 将方程(x+1)²+(x-2)(x+2)=1化成一元二次方程的一般形式，并写出其中的二次项、二次项系数；一次项、一次项系数；常数项．

　 列方程．　 问题(1)《九章算术》“勾股”章有一题：“今有户高多于广六尺八寸，两隅相去适一丈，问户高、广各几何？”

　　 如果假设门的高为x尺，那么，这个门的宽为_______尺，根据题意，得________．

　　 整理、化简，得：__________．

问题(2)如图，如果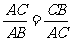，那么点C叫做线段AB的黄金分割点．

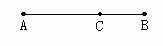
　　 如果假设AB=1，AC=x，那么BC=________，根据题意，得：________．

　　 整理得：_________．

　　 问题(3)有一面积为54m²的长方形，将它的一边剪短5m，另一边剪短2m，恰好变成一个正方形，那么这个正方形的边长是多少？

　　 如果假设剪后的正方形边长为x，那么原来长方形长是________，宽是_____，根据题意，得：_______．

　　 整理，得：________．

3、在实际问题转化为数学模型( 一元二次方程 ) 的过程中，体会学习一元二次方程的必要性和重要性。

布置作业：

2、一元二次方程的一般形式为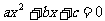(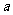≠0)，一元二次方程的项及系数都是根据一般式定义的，这与多项式中的项、次数及其系数的定义是一致的。

1、只含有一个未知数，并且未知数的最高次数是2的整式方程，叫做一元二次方程。

5．练习一 将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项

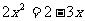　 　2x(x-1)=3(x-5)-4　　

练习二　 关于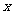的方程，在什么条件下是一元二次方程？在什么条件下是一元一次方程？

本课小结：