
2.已知方程5x2+mx-6=0的一个根是x=3,则m的值为________.
1.如果x2-81=0,那么x2-81=0的两个根分别是x1=________,x2=__________.
3.已知x=-1是方程ax2+bx+c=0的根(b≠0),则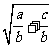 =(
).
=(
).
A.1 B.-1 C.0 D.2
2.方程ax(x-b)+(b-x)=0的根是( ).
A.x1=b,x2=a B.x1=b,x2=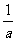 C.x1=a,x2=
C.x1=a,x2=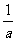 D.x1=a2,x2=b2
D.x1=a2,x2=b2
例3.要剪一块面积为150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应该怎样剪?
设长为xcm,则宽为(x-5)cm
列方程x(x-5)=150,即x2-5x-150=0 请根据列方程回答以下问题:
(1)x可能小于5吗?可能等于10吗?说说你的理由.
(2)完成下表:
|
x |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
… |
|
x2-5x-150 |
|
|
|
|
|
|
|
|
|
(3)你知道铁片的长x是多少吗?
作业设计 一、选择题
1.方程x(x-1)=2的两根为( ).
A.x1=0,x2=1 B.x1=0,x2=-1 C.x1=1,x2=2 D.x1=-1,x2=2
提问:(1)问题1中一元二次方程的解是多少?问题2中一元二次方程的解是多少?
(2)如果抛开实际问题,问题1中还有其它解吗?问题2呢?
老师点评:(1)问题1中x=6是x2-36=0的解,问题2中,x=10是x2+2x-120=0的解.
(3)如果抛开实际问题,问题(1)中还有x=-6的解;问题2中还有x=-12的解.
为了与以前所学的一元一次方程等只有一个解的区别,我们称:
一元二次方程的解叫做一元二次方程的根.
回过头来看:x2-36=0有两个根,一个是6,另一个是-6,但-6不满足题意;同理,问题2中的x=-12的根也满足题意.因此,由实际问题列出方程并解得的根,并不一定是实际问题的根,还要考虑这些根是否确实是实际问题的解.
例1.下面哪些数是方程2x2+10x+12=0的根?
-4,-3,-2,-1,0,1,2,3,4.
例2.你能用以前所学的知识求出下列方程的根吗?
(1)x2-64=0 (2)3x2-6=0 (3)x2-3x=0
解:
问题1.如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m,那么梯子的底端距墙多少米? 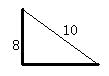
设梯子底端距墙为xm,那么,
根据题意,可得方程为___________.
整理,得_________.
列表:
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
|
|
|
|
|
|
|
|
|
|
|
|
问题2.一个面积为120m2的矩形苗圃,它的长比宽多2m,苗圃的长和宽各是多少?
设苗圃的宽为xm,则长为_______m.
根据题意,得________.
整理,得________.
列表:
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.一块矩形铁片,面积为1m2,长比宽多3m,求铁片的长,小明在做这道题时,是这样做的:
设铁片的长为x,列出的方程为x(x-3)=1,整理得:x2-3x-1=0.小明列出方程后,想知道铁片的长到底是多少,下面是他的探索过程:
第一步:
|
x |
1 |
2 |
3 |
4 |
|
x2-3x-1 |
-3 |
-3 |
|
|
所以,________<x<__________
第二步:
|
x |
3.1 |
3.2 |
3.3 |
3.4 |
|
x2-3x-1 |
-0.96 |
-0.36 |
|
|
所以,________<x<__________
(1)请你帮小明填完空格,完成他未完成的部分;
(2)通过以上探索,估计出矩形铁片的整数部分为_______,十分位为______.
2.关于x的方程(2m2+m)xm+1+3x=6可能是一元二次方程吗?为什么?
1.a满足什么条件时,关于x的方程a(x2+x)=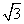 x-(x+1)是一元二次方程?
x-(x+1)是一元二次方程?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com