
4、例2、一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示.
分 析 我们知道:1纳米= 米.由
米.由 =10-9可知,1纳米=10-9米.
=10-9可知,1纳米=10-9米.
所以35纳米=35×10-9米.
而35×10-9=(3.5×10)×10-9
=35×101+(-9)=3.5×10-8,
所以这个纳米粒子的直径为3.5×10-8米.
3、探索:
10-1=0.1
10-2=
10-3=
10-4=
10-5=
归纳:10-n=
例如,上面例2(2)中的0.000021可以表示成2.1×10-5.
2、 类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10-n的形式,其中n是正整数,1≤∣a∣<10.
1、回忆: 在§2.12中,我们曾用科学记数法表示一些绝对值较大的数,即利用10的正整数次幂,把一个绝对值大于10的数表示成 a×10n的形式,其中n是正整数,1≤∣a∣<10.例如,864000可以写成8.64×105.
3、例1 计算(2mn2)-3(mn-2)-5并且把结果化为只含有正整数指数幂的形式。
解:原式= 2-3m-3n-6×m-5n10 =  m-8n4 =
m-8n4 = 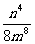
4 练习:计算下列各式,并且把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3.
2、概括:指数的范围已经扩大到了全体整数后,幂的运算法则仍然成立。
1、探 索
现在,我们已经引进了零指数幂和负整数幂,指数的范围已经扩大到了全体整数.那么,在§14.1“幂的运算”中所学的幂的性质是否还成立呢?与同学们讨论并交流一下,判断下列式子是否成立.
(1)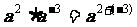 ; (2)(a·b)-3=a-3b-3;
(3)(a-3)2=a(-3)×2
; (2)(a·b)-3=a-3b-3;
(3)(a-3)2=a(-3)×2
2、(04苏州)不用计算器计算: ÷(-2)2 -2 -1+
÷(-2)2 -2 -1+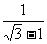
1、 ;
; = ;
= ; = ,
= , = ,
= , = 。
= 。
3. 若-3≤x≤2时,试化简│x-2│+ +
+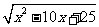 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com