
2.一元二次方程x2-ax+1=0的两实数根相等,则a的值为( ).
A.a=0 B.a=2或a=-2
C.a=2 D.a=2或a=0
1.以下是方程3x2-2x=-1的解的情况,其中正确的有( ).
A.∵b2-4ac=-8,∴方程有解
B.∵b2-4ac=-8,∴方程无解
C.∵b2-4ac=8,∴方程有解
D.∵b2-4ac=8,∴方程无解
2.选用课时作业设计.
第五课时作业设计
1.教材P46 复习巩固6 综合运用9 拓广探索1、2.
本节课应掌握:
b2-4ac>0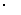 一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实根;b2-4ac=0
一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实根;b2-4ac=0 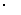 一元二次方程ax2+bx+c=0(a≠0)有两个相等的实根;b2-4ac<0
一元二次方程ax2+bx+c=0(a≠0)有两个相等的实根;b2-4ac<0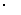 一元二次方程ax2+bx+c=0(a≠0)没有实数根及其它的运用.
一元二次方程ax2+bx+c=0(a≠0)没有实数根及其它的运用.
例2.若关于x的一元二次方程(a-2)x2-2ax+a+1=0没有实数解,求ax+3>0的解集(用含a的式子表示).
分析:要求ax+3>0的解集,就是求ax>-3的解集,那么就转化为要判定a的值是正、负或0.因为一元二次方程(a-2)x2-2ax+a+1=0没有实数根,即(-2a)2-4(a-2)(a+1)<0就可求出a的取值范围.
解:∵关于x的一元二次方程(a-2)x2-2ax+a+1=0没有实数根.
∴(-2a)2-4(a-2)(a+1)=4a2-4a2+4a+8<0
a<-2
∵ax+3>0即ax>-3
∴x<-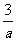
∴所求不等式的解集为x<-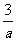
不解方程判定下列方程根的情况:
(1)x2+10x+26=0 (2)x2-x-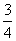 =0
=0
(3)3x2+6x-5=0
(4)4x2-x+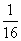 =0
=0
(5)x2-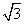 x-
x-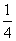 =0 (6)4x2-6x=0
=0 (6)4x2-6x=0
(7)x(2x-4)=5-8x
从前面的具体问题,我们已经知道b2-4ac>0(<0,=0)与根的情况,现在我们从求根公式的角度来分析:
求根公式:x=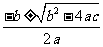 ,当b2-4ac>0时,根据平方根的意义,
,当b2-4ac>0时,根据平方根的意义,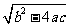 等于一个具体数,所以一元一次方程的x1=
等于一个具体数,所以一元一次方程的x1=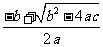 ≠x1=
≠x1=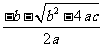 ,即有两个不相等的实根.当b2-4ac=0时,根据平方根的意义
,即有两个不相等的实根.当b2-4ac=0时,根据平方根的意义 =0,所以x1=x2=
=0,所以x1=x2=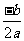 ,即有两个相等的实根;当b2-4ac<0时,根据平方根的意义,负数没有平方根,所以没有实数解.
,即有两个相等的实根;当b2-4ac<0时,根据平方根的意义,负数没有平方根,所以没有实数解.
因此,(结论)(1)当b2-4ac>0时,一元二次方程ax2+bx+c=0(a≠0)有两个不相等实数根即x1= ,x2=
,x2= .
.
(2)当b-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)有两个相等实数根即x1=x2=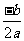 .
.
(3)当b2-4ac<0时,一元二次方程ax2+bx+c=0(a≠0)没有实数根.
例1.不解方程,判定方程根的情况
(1)16x2+8x=-3 (2)9x2+6x+1=0
(3)2x2-9x+8=0 (4)x2-7x-18=0
分析:不解方程,判定根的情况,只需用b-4ac的值大于0、小于0、等于0的情况进行分析即可.
解:(1)化为16x2+8x+3=0
这里a=16,b=8,c=3,b2-4ac=64-4×16×3=-128<0
所以,方程没有实数根.
(2)a=9,b=6,c=1,
b2-4ac=36-36=0,
∴方程有两个相等的实数根.
(3)a=2,b=-9,c=8
b2-4ac=(-9)2-4×2×8=81-64=17>0
∴方程有两个不相等的实根.
(4)a=1,b=-7,c=-18
b2-4ac=(-7)2-4×1×(-18)=121>0
∴方程有两个不相等的实根.
(学生活动)用公式法解下列方程.
(1)2x2-3x=0 (2)3x2-2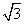 x+1=0
(3)4x2+x+1=0
x+1=0
(3)4x2+x+1=0
老师点评,(三位同学到黑板上作)老师只要点评(1)b2-4ac=9>0,有两个不相等的实根;(2)b2-4ac=12-12=0,有两个相等的实根;(3)b2-4ac=│-4×4×1│=<0,方程没有实根
5、练 习
①用科学记数法表示:
(1)0.000 03;(2)-0.000 0064;(3)0.000 0314;(4)2013 000.
②用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=_________秒;
(2)1毫克=_________千克;
(3)1微米=_________米; (4)1纳米=_________微米;
(5)1平方厘米=_________平方米; (6)1毫升=_________立方米.
[本课小结]:
引进了零指数幂和负整数幂,指数的范围扩大到了全体整数,幂的性质仍然成立。科学记数法不仅可以表示一个绝对值大于10的数,也可以表示一些绝对值较小的数,在应用中,要注意a必须满足,1≤∣a∣<10. 其中n是正整数
[布置作业]:课本第20页习题2、3;第22页复习题A3。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com